Shape Transformations | Definition, Examples, Types & Properties

Introduction

The boundary or an outline of an object is called its shape. We come across many shapes in our daily lives and kids start recognising these shapes even before actually studying about them. The alphabets of English shapes are all shapes of different types. The Sun, the earth and other planets, the mountains and all other things in the world are all of the specific shapes.

Definition

Shape transformations are changes done in the shapes on a coordinate plane. In other words, shape transformation means changing the position, size or aspect ratio of a shape. This can be done in a number of ways. Let us learn about some types of shape transformations.

Coordinate Plane

In order to understand different types of shape transformations, it is important to recall what we mean by coordinate plane. A Cartesian coordinate plane is a system that uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric elements. This plane is determined by two perpendicular lines, called the x-axis and the y-axis. Let us learn more about these lines.

Let X ‘ O X and Y ‘ O Y be two mutually perpendicular lines through a point O in the plane of a graph paper as shown below.

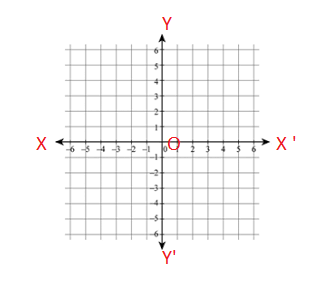
The line X O X ‘ is called the x-axis or axis of x and the line Y O Y ‘ is called the y-axis or the axis of y. The two lines X O X ‘ and Y O Y ‘ taken together are called the coordinate axis or the axis of the coordinate system. The point O is called the point of origin. This can also be represented as –

Quadrants of the Coordinate System

The x-axis and the y-axis together divide the entire coordinate system into four equal parts which are called the quadrants of the coordinate system.

For example, in the graph of the coordinate axis that we have defined above, the two lines X O X ‘ and Y O Y ‘ divide the plane of the graph paper into four regions, namely, X O Y, X ‘ O Y , X ‘ O Y ‘ and Y ‘ O X. These four regions are called the quadrants.

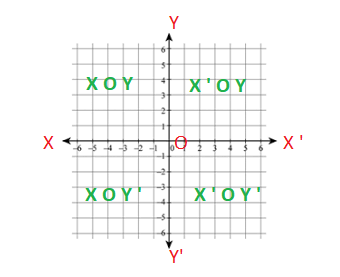
The ray O X ‘ is taken as a positive x-axis and the O X is taken as a negative x-axis. Similarly, the ray O Y is taken as a positive y-axis and the O y ‘ is taken as a negative y-axis. The signs of the x coordinate and the y coordinate in the four quadrants are thus defined as –

1 st Quatarant – x > 0 and y > 0

2 nd Quadrant – x < 0 and y > 0

3 rd Quarant – x < 0 and y < 0

4 th Quadrant – x > 0 and y < 0

Graphically, the values and x and y in the four quadrants can be represented as –

Types of Shape Transformations

There are four major types of transformations of functions. They are –

Translation
Rotation
Reflection
Dilation

Let us discuss them one by one.

Transformation of Shapes using Translation

Translation of shape means sliding the shape on a 2 – D plane. It is important to understand that a translation moves a shape up, down or from side to side but it does not change its appearance in any other way. Let us understand it using an example.

Consider the figure below –

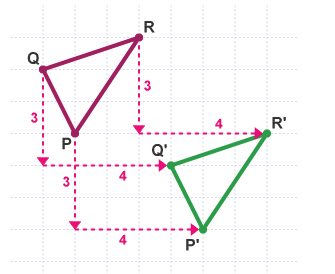
In the above figure, we can see that the triangle PQR has been translated to the triangle P’Q’R’. The triangle PQR has been translated 4 squares to the right and 3 squares down to obtain its news position P’Q’R’.

Properties of Transformation of Shapes using Translation

The following are the properties of Transformation of Shapes using Translation

The line segments are taken to line segments of the same length;
The angles are taken to angles of the same measure; and
The lines are taken to lines and parallel lines are taken to parallel lines.

How to translate a given shape?

Let us now understand how to translate a given shape. We shall do so through an example.

Consider the following rectangle –

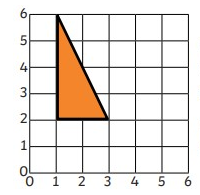
Suppose we want to translate this triangle to 3 squares to the right. How would we do this? The following steps shall be followed for this purpose –

The first step is to understand in which direction the shape needs to be translated. In our example, we need to translate it to the right.
The first step is to understand how many squares the shape needs to be translated. In our example, we need to translate it to 3 squares.
Now, that we have figured out the direction and the squares, we would translate it to the desired point. So, we will count 3 square to the right and move the shape at that point as shown below –

The triangle labelled 2 above is the translated form of the given triangle.

Important points while translating a shape to a particular point

The following points should always be kept in mind while translating a shape to a particular point –

The translation of a shape will move it up, down, left or right but the dimensions and appearance of the shape will stay the same.
In order to correctly translate a shape, each point must move at an equal distance.
It’s important to note that if a shape is made larger or smaller or is rotated this is not translation.

Transformation of Shapes using Rotation

Rotation in general terms is defined as the motion of an object around a centre or an axis. We can rotate different shapes by an angle around the centre point. Moreover, we can rotate a shape in both clockwise as well as anti-clockwise direction. Rotation turns a shape around a fixed point called the centre of rotation. It is important to note that rotations on a coordinate grid are considered to be anti-clockwise unless otherwise stated. Let us consider an example. In the figure below the object has been rotated to obtain the image

So, we can say that Rotation means turning. In mathematics, rotation means turning it about a given point, known as the centre of rotation. The point can be on the figure or at any point. Three things that are needed to describe a rotation are –

the direction of rotation which may be clockwise or anticlockwise
the angle of rotation and
the centre of rotation

Let us understand rotations through an example. Here we have the rotation of a square of about a given point the square has been further divided into colour squares so as to clearly understand its movement.

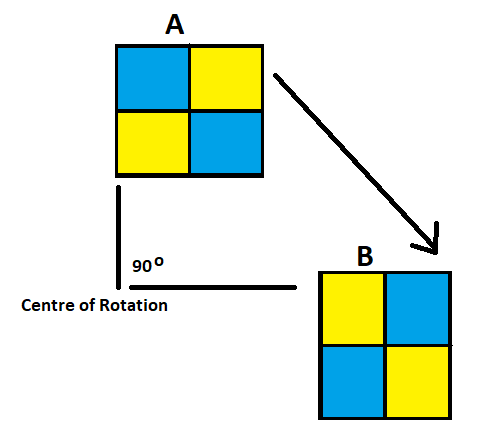
One Quarter Turn

In the above figure, shape A is rotated through an angle of 90 degrees at the point of the centre of rotation in the clockwise direction to get shape B. This movement is known as one-quarter turn, as we have moved the shape A at 90 degrees which is one-quarter of the complete circle, i.e. 360 degrees.

Now, again consider the figure below.

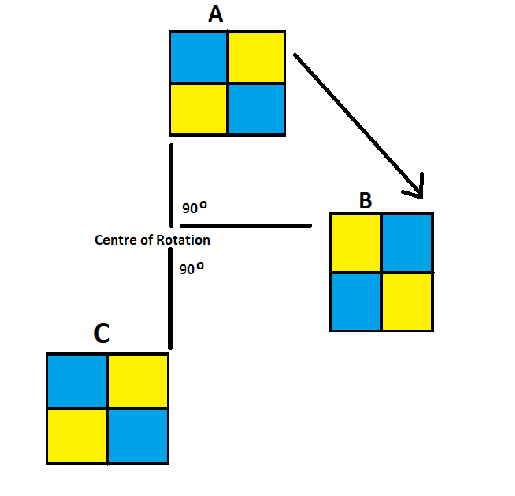
Half Turn

In this figure, the shape B is for rotated through an angle of 90 degrees about the same point of the centre of rotation in the clockwise direction to get the shape C. This is the same as if we would rotate shape A at an angle of 180 degrees about the point of the centre of rotation in the clockwise direction to get shape C. This movement is known as half turn, as we have moved the original shape A at 180 degrees which is half of the complete circle, i.e. 360 degrees.

Again, consider the figure below –

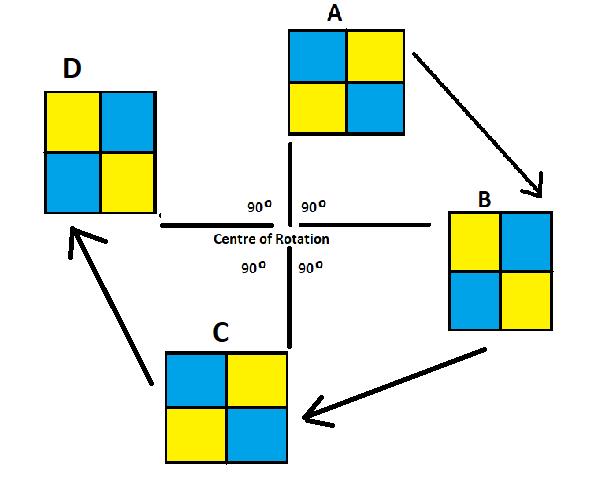
Three Quarter Turn

In the above figure the shape C is again rotated by an angle of 90 degrees about the point of the centre of rotation to get the shape D. This movement is known as three quarter turn, as we have moved the original shape A at 270 degrees which is three quarters of the complete circle, i.e. 360 degrees.

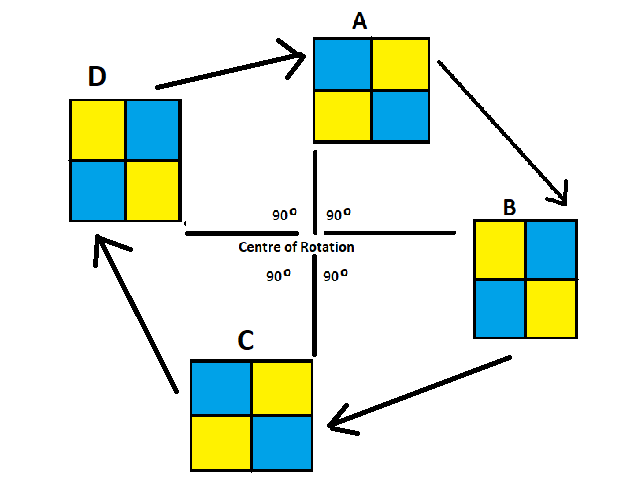
If the shape D is again rotated an angle of 90 degrees about the point of the centre of rotation, we will get back the shape A. This movement is known as the full turn, as we have moved the original shape A at 360 degrees which is a full turn of the complete circle, i.e. 360 degrees.

Angles of Rotation

The angle through which an object rotates ( turns ) about a fixed point is known as the angle of rotation. Depending upon the angle of rotation, these turns can be defined as –

Full Turn – An object is said to take a full turn if the angle of rotation is of 360^o.

Half Turn – An object is said to take a half turn, if the angle of rotation is of 180^o.

Three Quarters Turn – An object is said to take a three quarters turn if the angle of rotation is of 270^o.

Quarter Turn – An object is said to take a quarter turn, if the angle of rotation is of 270^o.

Centre of Rotation

The fixed point around which the object rotates is called the centre of rotation. This point could be inside the figure, in which case the figure will remain stationary and will just spin. Alternatively, the point could be outside the figure, causing the figure to move. For example, if a person spins the basketball on the tip of his finger, then the tip of his finger will be considered as rotational symmetry. Now, let us understand, what we mean by rotational symmetry.

Properties of Transformation of Shapes using Rotation

The following are the properties of Transformation of Shapes using Rotation

A rotation is a transformation that turns a figure about a fixed point called the centre of rotation.
An object and its rotation are the same shape and size, but the figures may be turned in different directions.
Rotations may be clockwise or anti – clockwise.

Formula of Rotation for different angles of Rotation

Type of Rotation	A point on the Image	A point on the Image after Rotation
Clockwise Rotation of 90°	( x, y )	( y, -x )
Anti – Clockwise Rotation of 90°	( x, y )	( -y, x )
Rotation of 180° ( This can be both Clockwise and anti – Clockwise )	( x, y )	( -x, -y )
Clockwise Rotation of 270°	( x, y )	( -y, x )
Anti – Clockwise Rotation of 270°	( x, y )	( y, -x )

Transformation of Shapes using Reflection

Reflection means finding the mirror image of a shape. In other words, it means swapping all pairs of points that are on exactly opposite sides of the line of reflection. A reflection is defined by the axis of symmetry or mirror line. Let us recall what we mean by axis or line of symmetry. We say that a given line has a line of symmetry or it is symmetrical about a line if the line divides a given figure into two identical halves. The line is called the axis of symmetry or line of symmetry.

Let us consider an example.

Suppose we have the following shape and we want to reflect it along the x – axis.

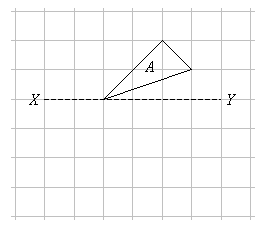
The following would be the reflection of the given shape –

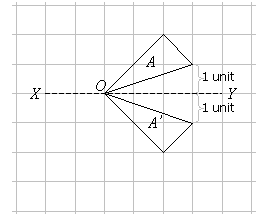
It is important to note here that the point O, which is the axis of reflection remains unchanged.

Properties of Transformation of Shapes using Reflection

The following are the properties of Transformation of Shapes using Reflection –

The image and the pre-image are of the same size and shape. This means that when reflected both the shape and its reflected image are congruent.
The line segment which connects the corresponding parts of the image and pre-image is perpendicular to the line of reflection.
The distance from the line of reflection of the corresponding parts of the image and pre-image is the same.

Reflection Symmetry

When we reflect a shape there are two types of line symmetries according to which we can classify the symmetries in different geometrical figures. These types are –

Horizontal Lines of Symmetry
Vertical Line of Symmetry

Horizontal Lines of Symmetry

If the line of symmetry is such that it divides a geometrical shape into two identical halves in a horizontal manner, it is known as a horizontal line of symmetry. In other words, a horizontal line of symmetry is that line that runs across the image thus dividing into two identical halves. This line may also be called a sleeping straight line that parts an image or shape into identical halves.

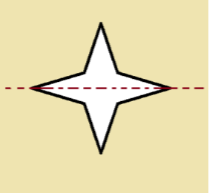
Vertical Line of Symmetry

If the line of symmetry is such that it divides a geometrical shape into two identical halves in a vertical manner, it is known as a vertical line of symmetry. In other words, a vertical line of symmetry is that line that runs down an image thus dividing it into two identical halves. This means that a vertical line of symmetry is a straight standing line that divides an image or shape into two identical halves.

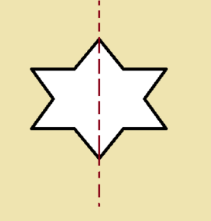
Transformation of Shapes using Dilation

A dilation is a transformation which preserves the shape and orientation of the figure, but changes its size. Let us consider an example. There are two possibilities in a dilation of a shape –

Stretch – In this transformation, the image grows larger

Shrink – In this transformation, the image grows smaller

Dilation scale Factor

The scale factor of a dilation is the factor by which each linear measure of the figure is multiplied. When dilating a shape P ( x, y ) with a scale factor, say k ( which is a constant ) we have

P ( x, y ) → P ‘ ( k x, k y )

This means that –

If the scale factor is more than 1, then the shape will stretch which means it will grow larger.
If the scale factor is between 0 and 1, then the image will shrink which means it will grow smaller.
If the scale factor is 1, then the original image and the image produced are congruent, i.e. same.

Let us understand it through an example.

Consider the following shapes –

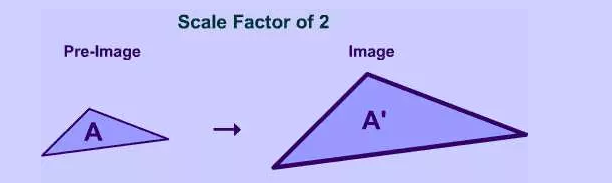
Note the difference in size of the two shapes. The image is twice its pre-image which means it has scale factor of 2.

Let us consider another example.

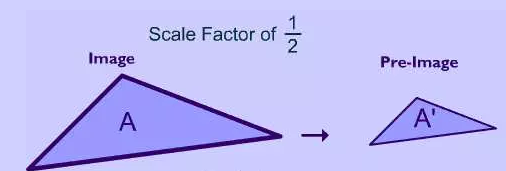
Note the difference in size of the two shapes. The image is half of the size of its pre-image which means it has scale factor of 1 /2.

Properties of Transformation of Shapes using Dilation

The following are the properties of Transformation of Shapes using Dilation –

Each angle of the shape remains the same
Midpoints of the sides of the figure remain the same as the midpoint of the dilated shape
Parallel and perpendicular lines in the figure remain the same as the parallel and perpendicular lines of the dilated figure
The shape remains the same

Key Facts and Summary

Shape transformations are changes done in the shapes on a coordinate plane.
Translation of shape means sliding the shape on a 2 – d plane.
A translation moves a shape up, down or from side to side but it does not change its appearance in any other way.
Rotation in general terms is defined as the motion of an object around a centre or an axis.
The fixed point around which the object rotates is called the centre of rotation.
Reflection means finding the mirror image of a shape.
A dilation is a transformation which preserves the shape and orientation of the figure, but changes its size.
The scale factor of a dilation is the factor by which each linear measure of the figure is multiplied.

Recommended Worksheets

Shape Transformation (Basic) (International Women’s Day Themed) Math Worksheets
Shape Transformations (International Literacy Day Themed) Math Worksheets
Congruent Shapes (World Tourism Day) Themed Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!