Collinear Points

Introduction

Geometrically speaking, collinearity is the property of points on a single, straight line. The phrase has been used more broadly to refer to a row of aligned objects or points. In this article, we will learn more about collinear points and how we prove that points are collinear using different formulas.

Grade Appropriateness

Collinear Points is a concept typically introduced around the 5th grade, and its understanding is deepened in the subsequent grades. Students between the ages of 8 and 15 (roughly corresponding to 3rd grade through 10th grade) should find this topic helpful and understandable.

Math Domain

This topic falls under Geometry, a crucial branch of Mathematics. It provides insights into the properties and relationships of points, lines, angles, and shapes.

Applicable Common Core Standards

Collinear points align with the following Common Core Standards:

CCSS.MATH.CONTENT.4.G.A.1: Draw points, lines, line segments, rays, angles (right, acute, obtuse), and perpendicular and parallel lines. Identify these in two-dimensional figures.

CCSS.MATH.CONTENT.5.G.A.1: Use a pair of perpendicular number lines, called axes, to define a coordinate system, with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates.

Definition of Collinear Points

Collinear points in geometry are those that are found along the same straight line. No matter how many points you have, if you can draw a single straight line that passes through all those points, those points are collinear.

Key Concepts

Collinear Points: If two points are given, they will always be collinear because a single line can pass through these two points.

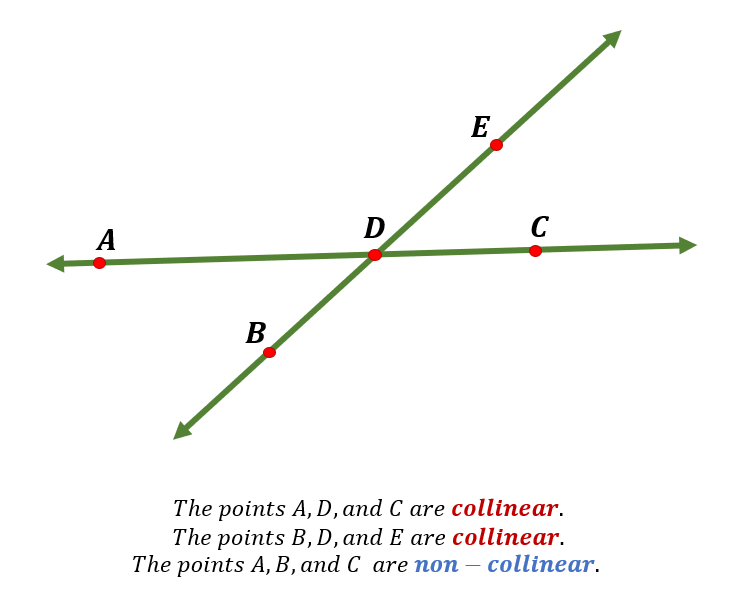
If there are three or more points, then those points may or may not be collinear. If a single straight line can be drawn passing through all three (or more) points, they are collinear; otherwise, they are non-collinear.

Discussion with Illustrative examples

Points that are located on a single straight line are called collinear points. In Euclidean geometry, two or more points are collinear if they are on the same line, even if they are close or apart.

The term Collinear is formed by two Latin words, ‘col,’ which means together, and ‘linear,’ which means line. Therefore, collinear points are points that lie on the same line. Here are some examples:

Remember that two points are always collinear. Hence, any two points in the figure below are collinear, like {AC}, {E, D}, {G, B}, etc.

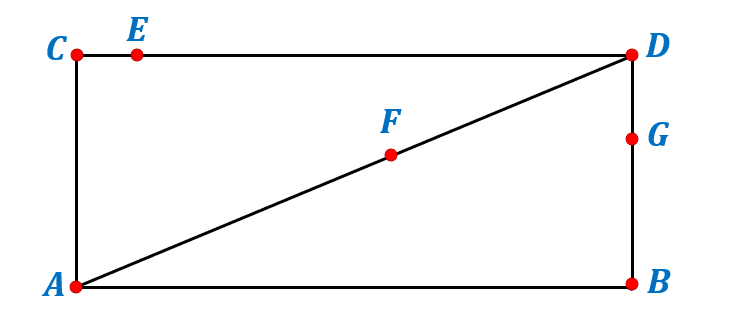
The other sets of collinear points in the figure are {A, F, D}, {C, E, D}, and {D, G, B}.

Other sets of points, such as {A, E, D}, {F, G, B}, {C, F, D}, {A, F, G, D}, etc., are called non-collinear points. Non-collinear points are those that do lie on the same line. Hence, we cannot draw a single straight line using these points.

Collinear Points Formula

Collinearity is the property of points being collinear.

Any three points or more will only be collinear if they lie in a straight line.

Only one line can go through three or more collinear points.

Slope Formula

This formula is used to find the slope of the lines formed by three points. If the slopes are equal, then the three points are collinear. Note: The slope of the line is the measure of the steepness of the line.

Suppose we have three points, A, B, and C. These points will be collinear if the:

Slope of line AB = slope of line BC = slope of line AC.

In calculating the slope of joining points, we use the formula:

m=$\frac{y_2-y_1}{x_2-x_1}$

So, to show that points A(1,3), B(5,4), and C(9,5) are collinear, we have,

$m_{AB}$ = $\frac{4-3}{5-1}m_{AB}$ = $\frac{1}{4}$

$m_{BC}$ = $\frac{5-4}{9-5}m_{BC}$ = $\frac{1}{4}$

$m_{AC}$ = $\frac{5-3}{9-1}m_{AC}$ = $\frac{2}{8}m_{AC}$ = $\frac{1}{4}$

The slopes of the three pairs are equal. Therefore, points A, B, and C are collinear.

Area of Triangle Formula

Three collinear points cannot form a triangle. Suppose we have points L(x₁,y₁), M(x₂,y₂), N(x₃,y₃).

We can prove that these points are collinear using this formula:

$\frac{1}{2}$|x₁(y₂-y₃)+x₂(y₃-y₁)+x₃(y₁-y₂)=0

Using this formula, you can determine whether the three points are collinear. If the area of the triangle is zero, then the points are considered collinear.

Let us say we want to calculate if A (0,-1), B(4,2), and C(8,5) are collinear points. When we substitute the coordinates in the formula and simplify our answer, we’ll have,

$\frac{1}{2}$|0(2 – 5) + 4(5-(-1)+8(-1-2)|

$\frac{1}{2}$|0(-3)+4(6)+8(-3)|

$\frac{1}{2}$|0+24-24|

$\frac{1}{2}$|(0)

Area=0

Since the area of the three points is 0, then A, B, and C are collinear.

Distance Formula

Three points are considered collinear if the sum of two distances equals the distance between the first and third points.

Distance from AB + Distance from BC = Distance from AC

d_AB + d_BC = d^AC

Using this formula, we find the distance between the three points, from the first to the second point and the second point to the third point.

We use the distance formula to know the distance between two points (x₁,y₁) and (x₂,y₂).

d= $\sqrt{(y_2-y_1)^2 + (x_2-x_1)^2}$

Let us use points A (0,-1), B(4,2), and C(8,5) given earlier and prove that they are collinear using the distance formula.

Distance from A to B
d_AB=$\sqrt{(2-(-1)^2+(4-0)^2}$
d_AB=$\sqrt{(3)^2+(4)^2}$
d_AB=$\sqrt{9+16}$
d_AB=$\sqrt{25}$
d_AB=5

Distance from B to C
d_BC=$\sqrt{5-22+8-42}$
d_BC=$\sqrt{(3)^2+(4)^2}$
d_BC=$\sqrt{9+16}$
d_BC=$\sqrt{25}$
d_BC=5

Distance from A to C
d_AC=$\sqrt{5–12+8-02}$
d_AC=$\sqrt{(6)^2+(8)^2}$
d_AC=$\sqrt{36+64}$
d_AC=$\sqrt{100}$
d_AC=10

Summing up the distance to check if the points are collinear:

d_AB + d_BC = d_AC

5+5=10

Therefore, A, B, and C are collinear points.

Examples with Solutions

Example 1

Show that the points A(1,2), B(2,3), and C(3,4) collinear.

Solution

To determine if these points are collinear, we can calculate the slope between any two points and see if the slope is the same for all pairs.

m=$\frac{y_2-y_1}{x_2-x_1}$ (Slope Formula)

m_AB=$\frac{3-2}{2-1}$ = 1 (Slope of AB)

m_BC=$\frac{4-3}{3-2}$ = 1 (Slope of BC)

Since the slopes are equal, points A, B, and C are collinear.

Example 2

Use the area triangle method to show if the points G(1,1), E(2,2), and F(3,5) are collinear or not.

Solution

Let us substitute the coordinates in the formula and calculate the area.

$\frac{1}{2}$|x₁(y₂ – y₃) + x₂(y₃ – y1) + x₃(y₁-y₂)|

$\frac{1}{2}$|1(2 – 5) + 2(5 – 1) + 3(1 – 2)|

$\frac{1}{2}$|1(-3) + 2(4) + 3(-1)|

$\frac{1}{2}$|-3+8-3|

$\frac{1}{2}$(2)

Area=1

Since the area is not zero, points G, E, and F are non-collinear.

Example 3

Show, using the distance formula method, that the following points are collinear: J(-2,6), K(1,5), and L(4,4).

Solution

Distance from J to K
d_JK=$\sqrt{(5-6)^2 + (1-(-2)^2}$
d_JK=$\sqrt{(-1)^2+(3)^2}$
d_JK=$\sqrt{1+9}$
d_JK=$\sqrt{10}$

Distance from K to L
d_KL=$\sqrt{(4-5)^2 + (4-1)^2}$
d_KL=$\sqrt{(-1)^2+(3)^2}$
d_KL=$\sqrt{1+9}$
d_KL=$\sqrt{10}$

Distance from J to L
d_JL=$\sqrt{(4-(-2)^2+(4-6)^2}$
d_JL=$\sqrt{(6)^2+(-2)^2}$
d_JL=36+4
d_JL=$\sqrt{40}$
d_JL=2$\sqrt{10}$

Summing up the distance to check if the points are collinear:

d_JK + d_KL = d_JL

$\sqrt{10}$+$\sqrt{10}$=2$\sqrt{10}$

Therefore, J, K, and L are collinear points.

Real-life Application with Solution

Understanding collinear points can help us in various real-world scenarios. For instance, imagine you’re helping your parents to plant trees in your backyard. Your parents want to plant three trees in a straight line. The positions of the first two trees (Tree A and B) are fixed. It would help if you found out where the third tree (Tree C) should be planted.

Let us say Tree A is at the point (1, 3), and Tree B is at (2, 5). If you want Tree C to be planted further at a distance of 1 unit on the x-axis, can you figure out its position for it to be collinear with A and B?

Slope_AB=$\frac{5-3}{2-1}$=2

To keep C collinear, we want to maintain the same slope. If C is at (3, y), the slope of BC should also be 2. So,

$\frac{y-5}{3-2}$ = 2

Solving this gives y = 7.

Therefore, Tree C should be planted at the point (3,7) to be in a straight line with Trees A and B.

Practice Test

Identify if the following sets of points are collinear.

a. M(0,0), N(2,2), and O(4,4)

b. X(1,1), Y(2,3), and Z(3,2)

c. A(-1,2), B(1,4), and C(2,6)

d. P(3,3), Q(6,6), and R(9,9)

e. D(1,1), E(3,2), and F(5,3)

Answers:

a. collinear

b. non-collinear

c. non-collinear

d. collinear

e. collinear

Frequently Asked Questions (FAQs)

Can two points be non-collinear?

No, two points are always collinear because a straight line can always pass through them.

Can collinear points be in a curved line?

No, collinear points must lie in a straight line.

What does it mean if three points are non-collinear?

If three points are non-collinear, they do not all lie on the same straight line.

What are the practical applications of collinear points?

Understanding collinear points can help design and arrange objects in a straight line, like arranging furniture in a room, planting trees in a row, aligning buttons on a user interface, and more.

Does the concept of collinear points apply only in 2D?

No, the concept of collinearity also applies in 3D space and even in higher dimensions. For instance, in 3D, three points are collinear if they lie on the same straight line.

Recommended Worksheets

Collinear Points (Construction Themed) Math Worksheets
Area of Triangles (Ice cream Themed) Worksheets
Graphing Proportional Relationships and Identifying Slope of the Line 8th Grade Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!