Introduction
Directed numbers are essential in mathematics, as they help us understand and solve problems involving positive and negative values. They are used in various areas of mathematics, including algebra, number theory, and coordinate geometry. This article shall provide an in-depth understanding of directed numbers, their importance, key concepts, and real-life applications.
Grade Appropriateness
Directed numbers are introduced in middle school mathematics, typically around 6th or 7th grade, and continue to be used throughout high school and beyond. As students progress through their math education, they encounter more complex applications of directed numbers.
Math Domain
Directed numbers fall within the domain of number theory, which deals with the properties and relationships of numbers. They are also widely used in algebra and coordinate geometry for representing quantities, positions, and operations on numbers.
Applicable Common Core Standards
Directed numbers are covered in the following Common Core State Standards for Mathematics:
6.NS.C.5: Understand that positive and negative numbers are used together to describe quantities having opposite directions or values.
6.NS.C.6: Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
7.NS.A.1: Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers.
Definition of Directed Numbers
Directed numbers are numbers that have a sign (positive or negative) associated with them. They help us represent quantities that can have opposing directions or values. Positive-directed numbers indicate a gain or movement in the positive direction, while negative-directed numbers represent a loss or movement in the negative direction.
Key Concepts
Number Line: A number line illustrates or represents directed numbers, with positive numbers on the right and negative numbers on the left.
Opposites: Two directed numbers are called opposites if they have the same magnitude (or value) but opposite signs.
Absolute Value: A directed number’s absolute value, disregarding its sign, is its distance from zero on the number line,
Adding and Subtracting Directed Numbers: To add or subtract directed numbers, use their signs to determine whether to combine their magnitudes or find the difference between them.
Discussion with Illustrative Examples
Directed numbers can be positive or negative numbers. These numbers are characterized by size (2 and 4.8) and direction ( – or +).
Positive numbers: +3, +1.5, +0.2, +2, …
Negative numbers: – 3, – 1.5, -0.2, -21, …
Remember:
+3 is read as “positive three.”
+1.5 is read as “positive one point five.”
-3 is read as “negative three.”
-0.2 is read as “negative zero point two.”
Operations Involving Directed Numbers
The following are the rules for dealing with addition, subtraction, multiplication, and division of directed numbers.
Addition
There are two rules:
1. SAK (Same sign – Add – Keep the sign)
Examples:
(-2) + (-3) = -5
(-3) + (-4) + (-1) = -8
2. DSB (Different sign – Subtract – copy the sign of the Bigger number)
Examples:
(-4) + (7) = 3
(2) + (-8) = -6
Subtraction
Change the sign of the subtrahend to its opposite, then change the operation to addition.
Examples:
(-3) – (5) = (-3) + (-5) = -8
Notice that the subtrahend, 5, was changed into -5, and then the operation was changed to addition.
Multiplication and Division
To multiply or divide integers, perform the operation as in whole numbers and then follow the rule for signs.
Same Signs: the answer is positive.
Different Signs: the answer is negative.
Examples:
(-2)(-3) = 6 (24) ÷ (-3) = – 8
(8)(-2) = -16 (-54) ÷ (-9) = 6
Examples with Solutions
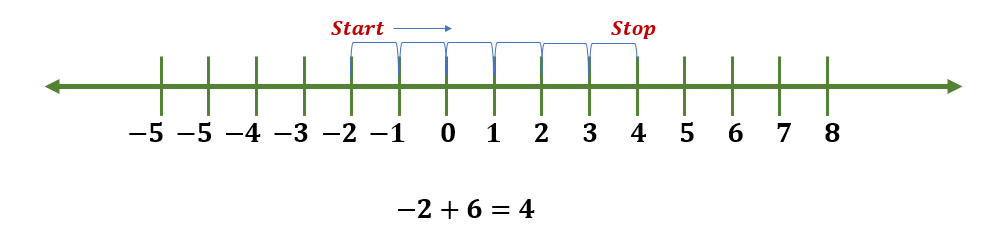
Example 1
Use the number line to solve -2+6.
Solution
Example 2
Find the sum of -7 and 5.
Solution
Since the numbers have different signs, we find the difference between their magnitudes: 7 – 5 = 2. The result will have the sign of the number with the larger magnitude, which is -7. So, the sum is -2.
Example 3
Subtract -4 from 3.
Subtracting -4 is the same as adding its opposite. The opposite of -4 is 4. So, we need to find the sum of 3 and 4, which is 7.
Example 4
Find the absolute value of -9.
Solution
The absolute value of -9 is the distance from -9 to 0 on the number line, which is 9.
Example 5
Add -3 and -6.
Solution
We add their magnitudes: 3 + 6= 9 since both numbers have the same sign
. The sum will have the same sign as the original numbers, which is negative. So, the sum is -9.
Example 6
Perform the indicated operations: (2 + -3) x (-8).
Solution
Let us simplify the parentheses first, then multiply.
(2 + -3) x (-8) =
(2 + -3) = -1
(-1) x (-8) = 8
Real-life Application with Solution
Directed numbers are values that have size and direction. Given this, the application of directed numbers is actually useful in our daily lives. Some of its common applications are:
Temperature – temperature readings have positive and negative measurements. That is why temperature is the most common example of how directed numbers can be used in real life.
Throughout the year, the temperature in some places in the US ranges from 21.5 ℃ to -3 ℃ (or 70.7 ℉ to 26.6 ℉).
Elevation above and below sea level – another good example of the application of directed numbers is the concept of elevation above and sea level.
Example Problem
A scuba diver starts at the water’s surface and then descends 40 feet below the surface. Later, the diver ascends 15 feet. What is the diver’s depth relative to the surface?
Solution
We can use directed numbers to represent the diver’s movement to solve this problem. Descending 40 feet is represented by – 40, and ascending 15 feet is represented by +15. To find the diver’s final depth, we add these directed numbers:
-40 + 15 = -40 + (+15) = -25
The diver is 25 feet below the surface.
Aside from temperature and elevation, directed numbers can also be applied to bank statements/accounts, floors below and above the ground floor of a building, goal scores expressed as above and below par, depths in a swimming pool, etc.
Practice Test
A. Answer each.
1. Add -8 and 3.
2. Subtract -5 from -2.
3. Find the absolute value of -11.
4. Subtract four from -7.
5. Add -4 and -7.
B. Perform the indicated operation(s).
1. (4 x -3) – 8 =
2. (-16 ÷ 4) + -3 =
3. (36 ÷ -4) + (-2 x -5) =
Frequently Asked Questions (FAQs)
What is the difference between a directed number and an integer?
A directed number is a number with an associated sign (positive or negative), while an integer is a whole number that can be negative, positive, or zero. All directed numbers are integers, but not all integers are directed numbers.
How do I multiply and divide directed numbers?
When multiplying or dividing directed numbers, the product or quotient will be positive if both numbers have the same sign; otherwise, it will be negative. Multiply or divide the magnitudes, then apply the appropriate sign to the result.
Why are directed numbers important in mathematics?
Directed numbers are essential for representing quantities that can have opposite directions or values, such as temperature changes, financial transactions, and positions on a coordinate plane. They also form the basis for understanding and solving problems involving signed numbers in various mathematical contexts.
Can direct numbers be fractions or decimals?
Yes, directed numbers can be fractions or decimals. Just like integers, fractions and decimals can have positive or negative signs associated with them.
What are the properties of directed numbers when performing operations?
When performing operations, some properties of directed numbers include the commutative, associative, and distributive properties. These properties hold true for addition and multiplication but not necessarily for subtraction and division.
Recommended Worksheets
Directed Numbers (Mayflower Day Themed) Math Worksheets
Adding Integers Using the Number Line (Easter Themed) Math Worksheets
Counting Coins (Grandparents’ Day Themed) Math Worksheets









