Introduction
Numbers that represent a portion of a whole are called fractions. Let us use the square below as an example.
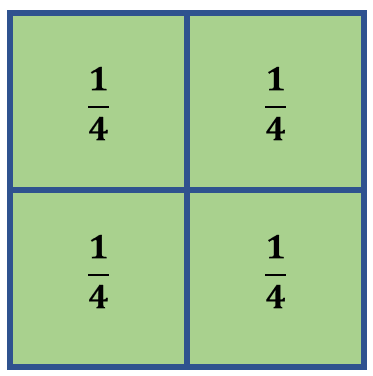
Since it has been cut into 4 equal parts, each piece represents one out of four. Mathematically, each piece is described as $\frac{1}{4}$. The number at the top is referred to as the numerator, and its bottom number is the denominator. $\frac{1}{4}$ is an example of a proper fraction because the denominator is greater than the numerator.
Otherwise, we will have an improper fraction when the numerator exceeds the denominator. Let us suppose that we instead have two squares and that each square is divided into four equal parts, as illustrated below.

There are 7 yellow parts out of 8 equal parts, which can be expressed as $\frac{7}{8}$. This number is an example of an improper fraction.
The topic of improper fractions will be explored in this article, along with methods for converting them to mixed fractions, simplifying them, and finding solutions to problems involving them.
What is an Improper Fraction?
Definition
When the numerator exceeds the denominator, the fraction is called improper. Suppose $\frac{a}{b}$ is an improper fraction; thus, a must be greater than b. Examples of improper fractions are $\frac{4}{3}$, $\frac{7}{4}$, $\frac{8}{5}$, and $\frac{11}{2}$.
A fraction has two main types, proper fractions and improper fractions. We have an improper fraction when the numerator is higher than the denominator; otherwise, it is a proper fraction.
Simplifying Improper Fractions
Simplifying improper fractions is the same thing as reducing the fractions. We do this by dividing the denominator and the numerator by their greatest common factor.
Let us say, for example; we have the improper fraction $\frac{18}{12}$. The numerator in the fraction is 18, while the denominator is 12. These are the factors of 18 and 12.
Factors of 18: { 2, 3, 6, 9 }
Factors of 12: { 2, 3, 4, 6 }
From the list above, the common factors of 18 and 12 are 2, 3, and 6. To simplify the $\frac{18}{12}$, we will use 6 as the divisor since it is the greatest common factor. Hence, we have,
$\frac{18÷6}{12÷6}$ = $\frac{3}{2}$
Therefore, $\frac{18÷6}{12÷6}$ is $\frac{3}{2}$ when simplified.
Improper Fraction vs Mixed Number
When the numerator exceeds the denominator, the fraction is called an improper fraction. A mixed number is a way of writing fractions that are greater than one. A whole number and a proper fraction make up a mixed number.
Examples of improper fractions are:
| $\frac{7}{5}$ | $\frac{9}{2}$ | $\frac{11}{7}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | $\frac{15}{4}$ |
| $\frac{31}{6}$ | $\frac{7}{4}$ | $\frac{12}{5}$ | $\frac{8}{3}$ | $\frac{17}{2}$ | $\frac{21}{4}$ |
Examples of mixed numbers are:
| 2$\frac{1}{5}$ | 4$\frac{2}{3}$ | 5$\frac{6}{11}$ | 3$\frac{2}{5}$ | 7$\frac{1}{2}$ | 6$\frac{3}{4}$ |
| 9$\frac{2}{7}$ | 10$\frac{1}{4}$ | 8$\frac{3}{5}$ | 6$\frac{7}{9}$ | 16$\frac{1}{3}$ | 5$\frac{9}{13}$ |
Improper Fraction Conversions
We can easily convert improper fractions to mixed numbers or decimals by following simple steps.
Converting Improper Fractions to Mixed Numbers
We shall divide the numerator by the denominator to make an improper fraction into a mixed number. To complete the mixed number, the quotient is the whole number part; the numerator is the remainder, while the divisor is the denominator.

For example, let us say that we must convert the improper fraction $\frac{23}{7}$ to a mixed number. When we divide 23 by 7, we will get 3 with the remainder of 2. We can form 3 equal groups of 7 with the remainder of 2. The image below illustrates the division process.
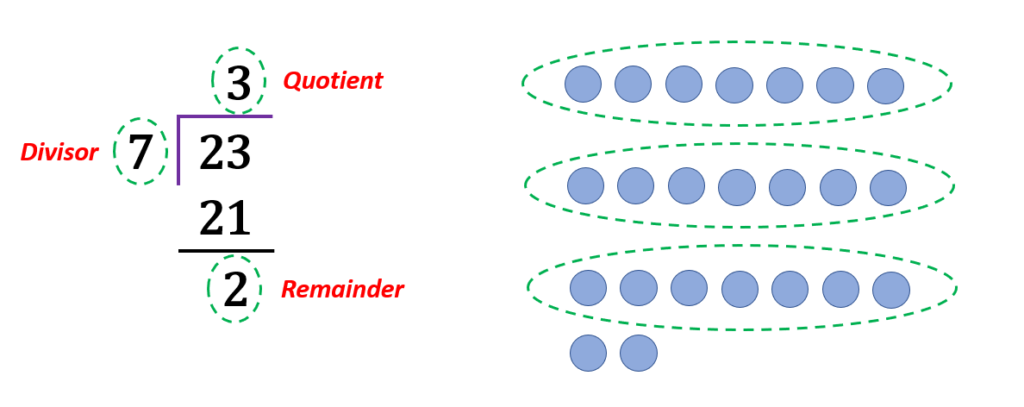
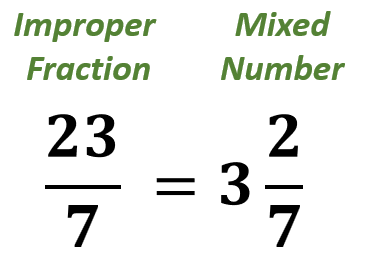
To form the equivalent mixed number, we will use the quotient ( 3 ) as the whole number part, and the fractional part is $\frac{2}{7}$. Notice that we use the same denominator.
$\frac{23}{7}$ =3$\frac{2}{7}$
To check the conversion, we must multiply the denominator by the whole number part and then add the answer to the numerator. The denominator stays the same. Hence, we have,
( 7 × 3 ) + 2 = 21 + 2 = 23
Therefore, the improper fraction $\frac{23}{7}$ is equal to 3$\frac{2}{7}$ in mixed number.
For another example, let us convert $\frac{9}{2}$ to a mixed number. When we divide 9 by 2, we will have 4 with the remainder of 1. The figure below shows the division process.

To check the conversion, we must multiply the denominator by the whole number part and then add the answer to the numerator. The denominator stays the same. Hence, we have,
( 2 × 4 ) + 1 = 8 + 1 = 9
Therefore, the improper fraction $\frac{9}{2}$ is equal to 4$\frac{1}{2}$ in mixed number.
Converting Improper Fractions to Decimals
To convert improper fractions to decimals, we must divide the numerator by the denominator. The process works the same way in converting improper fractions to mixed numbers.
For example, let us say that we must convert the improper fraction $\frac{11}{2}$ to decimals.

Therefore, $\frac{11}{2}$ is equal to 5.5 in decimals.
Addition and Subtraction of Improper Fractions
When adding or subtracting improper fractions, it is important to identify if you are adding or subtracting like or unlike terms. Like fractions have the same denominators; otherwise, they are unlike fractions. For example, $\frac{4}{3}$ and $\frac{5}{3}$ are like improper fractions, while $\frac{5}{4}$ and $\frac{7}{6}$ are unlike improper fractions.
Adding Like Improper Fractions
To add like improper fractions, we must add the numerators of the given fractions and then copy the same denominator. Simplify the answer when necessary.
Let us say, for example, let us add the like improper fractions $\frac{7}{4}$ and $\frac{9}{4}$. Hence we have,
$\frac{7}{4}$+$\frac{9}{4}$=$\frac{16}{4}$
Since $\frac{16}{4}$ can still be simplified, the sum of $\frac{7}{4}$ and $\frac{9}{4}$ is equal to 16.
For another example, let us say we have $\frac{11}{3}$+$\frac{14}{3}$. Since they have the same denominators, it is easy to get the sum of these fractions by adding the numerators and copying the same denominator.
$\frac{11}{3}$+$\frac{14}{3}$=$\frac{25}{3}$
Thus, the sum of $\frac{11}{3}$ and $\frac{14}{3}$ is equal to $\frac{25}{3}$.
Adding Unlike Improper Fractions
To add unlike improper fractions, we must first make the given improper fractions into proper fractions, then proceed to the process of adding like fractions. Identifying the least common multiple ( LCM ) of the denominators in converting the improper fraction to proper fractions is important. Then, simplify the fraction when needed.
Let us say, for example, we have the $\frac{5}{2}$+$\frac{13}{6}$.
Let us first make the given fractions to like improper fractions by identifying the LCM of the denominators.
Multiples of 2 are: { 2, 4, 6, 10, 8, 12, 14, 16, 18, 20, … }
Multiples of 6 are: { 6, 12, 24, 18, 36 30, 40, … }
From the list, 6, 12, and 18 are the common multiples, but we have to get the least common multiple ( LCM ), which is 6.
Thus, to make the given improper fractions into proper fractions, we must identify the numbers to multiply to these fractions, making the denominators equal to 6.
Hence, we have,
$\frac{5}{2}$ × $\frac{3}{3}$ = $\frac{15}{6}$
$\frac{13}{6}$ × $\frac{1}{1}$ = $\frac{13}{6}$
We shall then add the fractions $\frac{15}{6}$ and $\frac{13}{6}$ and add like fractions.
$\frac{15}{6}$+$\frac{13}{6}$=$\frac{28}{6}$
Since $\frac{28}{6}$ can still be simplified since 28 and 6 are divisible by 2, we have $\frac{28÷2}{6÷2}$=$\frac{14}{3}$.
Therefore $\frac{5}{2}$+$\frac{13}{6}$=$\frac{14}{3}$.
Subtracting Like Improper Fractions
To subtract like improper fractions, we must subtract the numerators of the given fractions and then copy the same denominator. Simplify the answer when necessary.
Let us say, for example, we subtract the like improper fractions $\frac{12}{5}$ and $\frac{9}{5}$. Hence we have,
$\frac{12}{5}$-$\frac{9}{5}$=$\frac{3}{5}$
Therefore, the difference between $\frac{12}{5}$ and $\frac{9}{5}$ is equal to $\frac{3}{5}$.
For another example, let us say we have $\frac{10}{7}-\frac{8}{7}$. Since they have the same denominators, it is easy to get the sum of these fractions by subtracting the numerators and copying the same denominator.
$\frac{10}{7}$-$\frac{8}{7}$=$\frac{2}{7}$
Thus, the difference between $\frac{10}{7}$ and $\frac{8}{7}$ is equal to $\frac{2}{7}$.
Subtracting Unlike Improper Fractions
To subtract, unlike improper fractions, we must first make the given improper fractions into proper fractions, then proceed to the process of subtracting like fractions. Finding the denominators’ least common multiple (LCM) is crucial for converting an improper fraction to a proper fraction. Then, simplify the fraction when needed.
Let us say, for example, we have the $\frac{15}{4}-\frac{9}{5}$.
Let us first make the given fractions to like improper fractions by identifying the LCM of the denominators.
Multiples of 4 are: { 4, 8, 16, 12, 20, 24, 28, 32, 36, 40, … }
Multiples of 5 are: { 5, 15, 10, 20, 25, 30, 35, 40, … }
From the list, 20 and 40 are the common multiples of 4 and 5. but we have to get the least common multiple ( LCM ), which is 20.
Thus, to make the given improper fractions into proper fractions, we must identify the numbers to multiply to these fractions, which will make the denominators equal to 20.
Hence, we have,
$\frac{15}{4}$ × $\frac{5}{5}$ = $\frac{75}{20}$
$\frac{9}{5}$ × $\frac{4}{4}$ = $\frac{36}{20}$
We shall then subtract the fractions $\frac{45}{20}$ and $\frac{36}{20}$ and proceed to add like fractions.
$\frac{75}{20}$ – $\frac{36}{20}$ = $\frac{39}{20}$
Therefore $\frac{15}{4}$ – $\frac{9}{5}$ = $\frac{39}{20}$.
Multiplying Improper Fractions
When multiplying improper fractions, we must obtain the product of the numerators of the provided fractions over the product of the denominators. And then simply the answer when necessary.
Let us say, for example; we have $\frac{7}{5}$ x $\frac{9}{8}$.
To get the product, we must multiply the numerators 7 and 9 and then multiply the denominators 5 and 8. Thus,
$\frac{7}{5}$ x $\frac{9}{8}$ =6340
Since 63 and 40 do not have common factors, $\frac{63}{40}$ is simplified already.
Thus, $\frac{7}{5}$ x $\frac{9}{8}$ is equal to $\frac{63}{40}$.
More Examples
Example 1
Which of the following are improper fractions?
| $\frac{1}{3}$ | $\frac{7}{2}$ | $\frac{11}{7}$ | $\frac{9}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
| $\frac{7}{15}$ | $\frac{5}{12}$ | $\frac{12}{5}$ | $\frac{5}{3}$ | $\frac{3}{5}$ | $\frac{21}{4}$ |
Solution
When the denominator exceeds the numerator, we have a proper fraction; otherwise, it is improper. Hence, the improper fractions above are as follows:
| $\frac{7}{2}$ | $\frac{11}{7}$ | $\frac{9}{4}$ | $\frac{12}{5}$ | $\frac{5}{3}$ | $\frac{21}{4}$ |
In each of the improper fractions, we have,
7 > 2 ; 11 > 7; 9 > 4
12 > 5 ; 5 > 3 ; 21 > 4
Example 2
Convert the following improper fractions to mixed numbers.
( a ) $\frac{7}{3}$ ( b ) $\frac{16}{5}$ ( c ) $\frac{27}{2}$ ( d ) $\frac{39}{4}$ ( e ) $\frac{50}{11}$
Solution
The improper fractions can be converted into mixed numbers by simply dividing the numerator by the denominator. To complete the mixed number, the quotient is the whole number part, while the numerator is the remainder. The denominator is the divisor or the same denominator of the given improper fraction.
( a ) $\frac{7}{3}$
When we divide 7 by 3, we will have 2 as the quotient and 1 as the remainder. Therefore, the improper fraction $\frac{7}{3}$ is equal to 2$\frac{1}{3}$ in mixed number.
( b ) $\frac{16}{5}$
When we divide 16 by 5, we will have 3 as the quotient and 1 as the remainder. Therefore, the improper fraction $\frac{16}{5}$ is equal to 3$\frac{1}{5}$ in mixed number.
( c ) $\frac{27}{2}$
When we divide 27 by 2, we will have 13 as the quotient and 1 as the remainder. Therefore, the improper fraction $\frac{27}{2}$ is equal to 13$\frac{1}{2}$ in mixed numbers.
( d ) $\frac{39}{4}$
When we divide 39 by 4, we will have 9 as the quotient and 3 as the remainder. Therefore, the improper fraction $\frac{39}{4}$ is equal to 9$\frac{3}{4}$ in mixed numbers.
( e ) $\frac{50}{11}$
When we divide 50 by 11, we will have 4 as the quotient and 6 as the remainder. Therefore, the improper fraction $\frac{50}{11}$ is equal to 4$\frac{6}{11}$ in mixed numbers.
Example 3
Write the following mixed numbers to improper fractions.
( a ) 2$\frac{3}{5}$ ( b ) 3$\frac{9}{11}$ ( c ) 7$\frac{4}{7}$ ( d ) 5$\frac{5}{9}$ ( e ) 12$\frac{1}{4}$
Solution
When we convert a mixed number into an improper fraction, we must multiply the denominator by the whole number part and then add the result to the numerator. The improper fraction and the mixed number have the same denominator.
( a ) 2$\frac{3}{5}$
We must multiply the denominator, 5, by the whole number part, 2. The product of 5 and 2 is10, then add the numerator, 3, which results in 13. Hence, we have ( 5 × 2 ) + 3 = 13. The answer gives the numerator of the improper fraction and then uses the same denominator.
2$\frac{3}{5}$= $\frac{(2×5)+3}{5}$=$\frac{13}{5}$
Therefore, the mixed number 2$\frac{3}{5}$ is equal to $\frac{13}{5}$ in improper fraction.
( b ) 3$\frac{9}{11}$
We must multiply the denominator, 11, by the whole number part, 3. The product of 3 and 11 is 33, then add the numerator 9, which results in 42. Hence, we have ( 11 × 3 ) + 9 = 42. The answer forms the numerator of the improper fraction and then copies the same denominator.
3$\frac{9}{11}$= $\frac{(11×3) +9}{11}$=$\frac{42}{11}$
Therefore, the mixed number 3$\frac{9}{11}$ is equal to $\frac{42}{11}$ in improper fraction.
( c ) 7$\frac{4}{7}$
We must multiply the denominator, 7, by the whole number part, 7. The product of 7 and 7 is 49, then add the numerator 4, which results in 53. Hence, we have ( 7 × 7 ) + 4 = 53. The answer forms the numerator of the improper fraction and then copies the same denominator.
7$\frac{4}{7}$= $\frac{(7×7) +4}{7}$=$\frac{53}{7}$
Therefore, the mixed number 7$\frac{4}{7}$ is equal to $\frac{53}{7}$ in improper fraction.
( d ) 5$\frac{5}{9}$
We must multiply the denominator, 9, by the whole number part, 5. The product of 5 and 9 is 45, then add the numerator, 5, which results in 50. Hence, we have ( 9 × 5 ) + 5 = 50. The answer forms the numerator of the improper fraction and then copies the same denominator.
5$\frac{5}{9}$= $\frac{(9×5) +5}{9}$=$\frac{50}{9}$
Therefore, the mixed number 5$\frac{5}{9}$ is equal to $\frac{50}{9}$ in improper fraction.
( e ) 12$\frac{1}{4}$
We must multiply the denominator, 4, by the whole number part, 12. The product of 4 and 12 is 48, then add the numerator 1, which results in 49. Hence, we have ( 4 × 12 ) + 1 = 49. The answer forms the numerator of the improper fraction and then copies the same denominator.
12$\frac{1}{4}$= $\frac{(4×12) +1}{4}$=$\frac{49}{4}$
Therefore, the mixed number 12$\frac{1}{4}$ is equal to $\frac{49}{4}$ in improper fraction.
Example 4
Perform the indicated operations and simplify.
( a ) $\frac{5}{3}$+$\frac{8}{3}$
( b ) $\frac{16}{5}$-$\frac{9}{5}$
( c ) $\frac{7}{4}$ x $\frac{5}{3}$
( c ) $\frac{5}{2}$ x $\frac{8}{3}$
Solution
( a ) $\frac{4}{3}$+$\frac{8}{3}$=$\frac{12}{3}$=4
( b ) $\frac{16}{5}$ – $\frac{9}{5}$=$\frac{7}{5}$
( c ) $\frac{7}{4}$ x $\frac{5}{3}$ = $\frac{35}{12}$
( c ) $\frac{5}{2}$ x $\frac{8}{3}$ = $\frac{40}{6}$ = $\frac{20}{3}$
Summary
Numbers that represent a portion of a whole are called fractions.
When the numerator exceeds the denominator, the fraction is called an improper fraction. Suppose $\frac{a}{b}$ is an improper fraction; thus, a must be greater than b.
Examples of improper fractions are:
| $\frac{7}{5}$ | $\frac{9}{2}$ | $\frac{11}{7}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | $\frac{15}{4}$ |
| $\frac{31}{6}$ | $\frac{7}{4}$ | $\frac{12}{5}$ | $\frac{8}{3}$ | $\frac{17}{2}$ | $\frac{21}{4}$ |
A mixed number is a way of writing fractions that are greater than one. A whole number and a proper fraction make up a mixed number.
Examples of mixed numbers are:
| 2$\frac{1}{5}$ | 4$\frac{2}{3}$ | 5$\frac{6}{11}$ | 3$\frac{2}{5}$ | 7$\frac{1}{2}$ | 6$\frac{3}{4}$ |
| 9$\frac{2}{7}$ | 10$\frac{1}{4}$ | 8$\frac{3}{5}$ | 6$\frac{7}{9}$ | 16$\frac{1}{3}$ | 5$\frac{9}{13}$ |
To create a mixed number from an improper fraction, divide the numerator by the denominator. To form the mixed equivalent mixed number, the quotient is the whole number part; the numerator is the remainder, while the divisor is the denominator.

Simplifying Improper Fractions
Simplifying improper fractions is the same thing as reducing the fractions. We do this by dividing the denominator and the numerator by their greatest common factor.
Frequently Asked Questions on Improper Fractions ( FAQs )
How do proper and improper fractions differ from one another?
Numbers that represent a portion of a whole are called fractions. Fractions are written with a numerator, a fraction bar, and a denominator. When the denominator is greater than the numerator, we have a proper fraction; otherwise, it is improper.
Examples of proper fractions ( Numerator < Denominator )
| $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{2}{7}$ | $\frac{5}{6}$ | $\frac{7}{11}$ | $\frac{13}{17}$ |
| $\frac{31}{6}$ | $\frac{7}{4}$ | $\frac{12}{5}$ | $\frac{8}{3}$ | $\frac{17}{2}$ | $\frac{21}{4}$ |
Examples of improper fractions ( Numerator > Denominator )
| $\frac{31}{6}$ | $\frac{7}{4}$ | $\frac{12}{5}$ | $\frac{8}{3}$ | $\frac{17}{2}$ | $\frac{21}{4}$ |
How do you convert mixed numbers to improper fractions?
A mixed number has two parts: the whole number and the proper fraction. To make a mixed number into an improper fraction, we must multiply the denominator by the whole number part, then add the answer to the numerator. The denominator stays the same.
For example, let us say that we must convert the mixed number 5$\frac{2}{3}$ to an improper fraction. We will have,
( 3× 5 ) + 2 = 15 + 2 = 17 , this is the numerator of the improper fraction
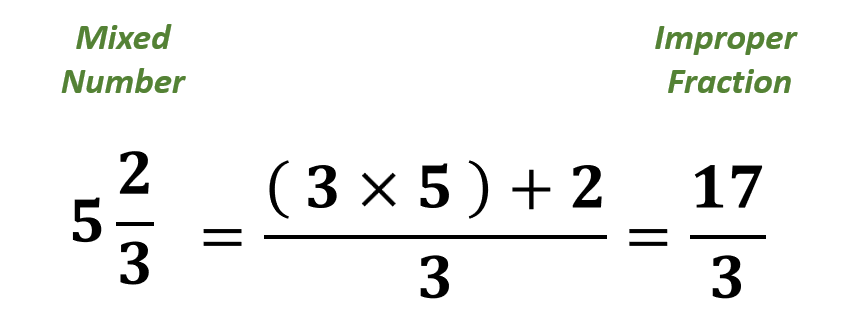
Therefore, the mixed number 5$\frac{2}{3}$ is equal to $\frac{17}{3}$.
How do like and unlike fractions
differ from one another?
If two fractions have the same denominator, they are said to be like; otherwise, they are unlike.
Examples of like fractions ( same denominators )
$\frac{5}{2}$ and $\frac{3}{2}$ are like fractions.
$\frac{9}{7}$ and $\frac{10}{7}$ are like fractions.
Examples of unlike fractions ( different denominators )
$\frac{11}{3}$ and $\frac{11}{2}$ are unlike fractions.
$\frac{12}{5}$ and $\frac{16}{9}$ are unlike fractions.
How do we simplify improper fractions?
When simplifying improper fractions is the same thing as reducing the fractions. We do this by dividing the denominator and the numerator by their greatest common factor.
Let us say, for example; we have the improper fraction $\frac{50}{10}$. Since the greatest common factor of 10 and 50 is 10, we have,
$\frac{50÷10}{10÷10}$ = $\frac{5}{1}$ = 5
Therefore, the simplified form of $\frac{50}{10}$ is 5.
How do we add and subtract improper fractions?
When adding or subtracting improper fractions, it is important to identify if you are adding or subtracting like or unlike terms. Like fractions have the same denominators; otherwise, they are unlike fractions. For example, $\frac{4}{3}$ and $\frac{5}{3}$ are like improper fractions, while $\frac{5}{4}$ and $\frac{7}{6}$ are unlike improper fractions.
To add like improper fractions, we must add the numerators of the given fractions and then copy the same denominator. Simplify the answer when necessary.
When adding unlike improper fractions, it is important to make the fractions proper using the least common multiple ( LCM ) of the denominators. Then, proceed to the process of adding like fractions.
How to multiply improper fractions?
When multiplying improper fractions, we must obtain the product of the numerators of the provided fractions over the product of the denominators. And then simply the answer when necessary.
Let us say, for example; we have $\frac{10}{2}$ x $\frac{5}{3}$.
To get the product, we must multiply the numerators 10 and 5, then multiply the denominators 2 and 3. Thus,
$\frac{10}{2}$ × $\frac{5}{3}$ = $\frac{50}{6}$
Since 2 is the greatest common factor of 50 and 6, $\frac{50}{6}$ can be simplified as $\frac{25}{3}$.Thus, $\frac{10}{2}$ × $\frac{5}{3}$ is equal to $\frac{25}{3}$.
Recommended Worksheets
Proper and Improper Fractions (Winter Themed) Math Worksheets
Subtraction of Improper Fractions (Construction Themed) Worksheets
Multiplication of Improper Fractions (Mother’s Day Themed) Worksheets









