What to expect in this article?
After reading this article, you will be able to define a number line and a fraction. This lesson will help you understand how different types of fractions are presented on a number line. Additionally, you will be able to define equivalent fractions and how we can show the equivalency of fractions on a number line. Furthermore, you will be able to practice and enhance your skills in representing fractions on a number line by answering the worksheets provided at the end of this page and using the resources for this topic.
What is a number line?
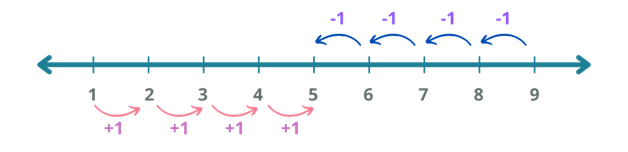
A number line is a straight line with numbers placed at equal intervals or segments along its length. A number line is infinitely extendible in any direction and is usually represented horizontally.
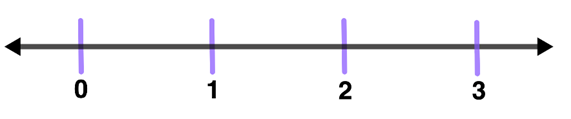
The image below is an example of how we can represent counting numbers in a number line.

The numbers on a number line increase as we move from left to right and decrease as we move from left to right.
What is a fraction?
A fraction denotes a portion of a whole. Fraction came from the Latin word “fractus,” which means broken. Hence, we can say that a fraction broke down a whole in an equal number of pieces. More so, a fraction denotes the number of pieces of a certain size, such as one-fourth, one-eight, eight-fifths, or three-quarters.
Consider a whole pizza that is cut into 8 equal slices.

Each slice of pizza can be expressed as a fraction. Say, for example, you get one piece of pizza. We can say that you have one-eight of pizza.
The denominator of a fraction represents how many equal parts the whole is divided into, while the numerator represents the amount of those parts. Fractions can be classified depending on the numbers written on the numerator and denominator.
Proper fraction
A fraction is said to be a proper fraction when the numerator and denominator are both positive, and the numerator is less than the denominator.
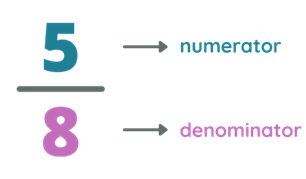
Given the proper fraction $\frac{5}{8}$, 5 is the numerator and 8 is the denominator. Since the numerator, 5, is less than the denominator, 8, then we are certain that this is a proper fraction
Improper fraction
A fraction is considered as an improper fraction when the numerator and denominator are both positive, and the numerator is greater than the denominator.
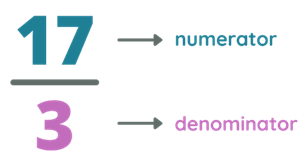
Consider the improper fraction $\frac{17}{3}$, 17 is the numerator while 3 is the denominator. Since the numerator, 17, is greater than the denominator, 3, then we can say that this is an improper fraction.
Mixed Number
A mixed number is a number expressed as the combination of a whole number and fraction.
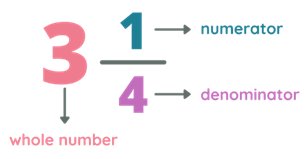
In this example, we can see that 3 is the whole number, $\frac{1}{4}$ is the fraction of the mixed number where 1 is the numerator and 4 is the denominator.
How to represent fractions on a number line?
Different types of fractions have different images on a number line. You must take note that fractions are always between two numbers.
To represent fractions on a number line, you may follow these steps:
- Draw a number line with whole numbers.
- Draw a number line with equal distances between whole numbers. The number of lines depends on the denominator of the fraction. Say, for example, a fraction with a denominator of 5 should have 4 equal segments between each whole number.
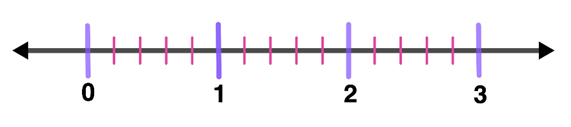
- Write the fractions with the denominator on the equal number of segments.

- Write the numerator the same as writing the counting numbers.
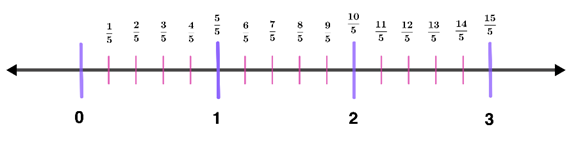
- Shade the fractional part from 0.
Proper fractions on a number line
A proper fraction is always between 0 and 1. Hence, you can represent a proper fraction on a number line by following the given steps:
- Draw a number line from 0 to 1.

- Draw a number line with equal distances between whole numbers. The number of lines between 0 and 1 depends on the denominator of the fraction. Consider a fraction with a denominator of 4. To represent it on a number line, we need to create 3 equal segments between 0 and 1.
- Write the fractions with the denominator on the equal number of segments.

- Write the numerator the same as writing the counting numbers.

- Shade the fractional part from 0.
Example #1
Represent $\frac{1}{7}$ on a number line.
Solution
To represent $\frac{1}{7}$ on a number line,
Step 1: Draw a number line from 0 to 1.

Step 2: Draw a number line with equal distances between 0 and 1. Since the denominator is 7, we need to create 6 equal distances of segments between the two numbers. Hence,
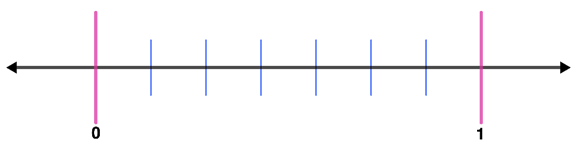
Step 3: Write the fractions on each segment.
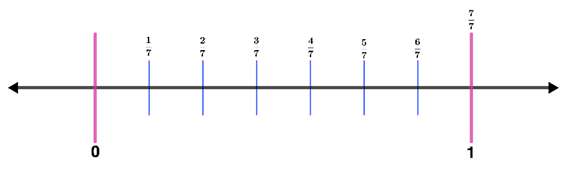
Step 4: Shade the number line from 0 to . Thus,
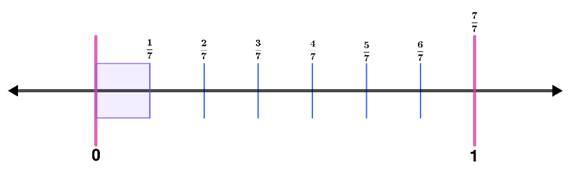
Therefore, $\frac{1}{7}$ looks like the image above when represented in a number line.
This example is an example of unit fractions. When we say unit fractions, these are proper fractions that have a numerator of 1.
Example #2
Represent $\frac{3}{8}$ on a number line.
Solution
Step 1: Draw a number line from 0 to 1.

Step 2: Draw a number line with equal distances between 0 and 1. Since the denominator is 8, we need to create 7 equal distances of segments. Hence,
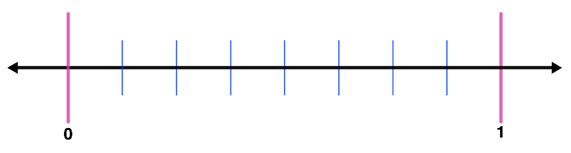
Step 3: Write the fractions on each segment.
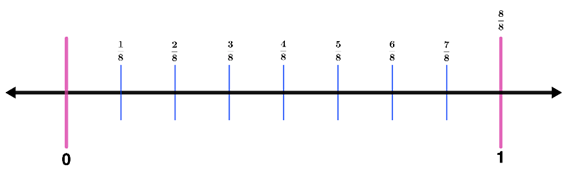
Step 4: Shade the number line from 0 to $\frac{3}{8}$. Thus,
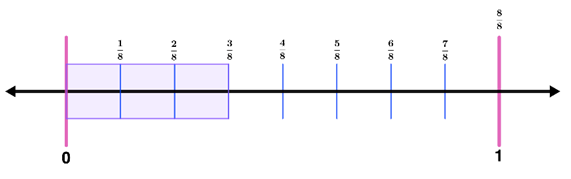
Therefore, $\frac{3}{8}$ looks like the image above when represented in a number line.
Improper fractions on a number line
Improper fractions when represented in a number line can be between any whole numbers. To represent improper fractions on a number line, consider the following steps below:
- Determine the whole numbers by dividing the numerator by the denominator.
- Draw a number line with equal distances between 0 to any whole number.
- Write the fractions with the denominator on the segments created.
- Write the numerator the same as writing the counting numbers.
- Shade the fractional part from 0.
Example
How can we represent $\frac{11}{6}$ on a number line?
Solution
Step 1: Determine how many whole numbers we should draw by dividing 11 by 6. Since $\frac{11}{6}$ can be found between 1 and 2, we will create a number line from 0 to 2.
Step 2: Draw a number line from 0 to 2.
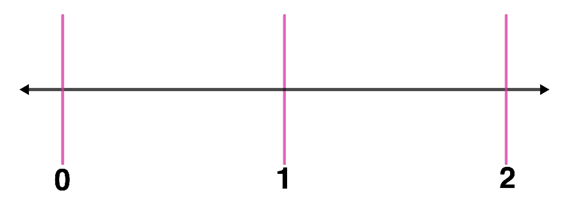
Step 3: Draw equal number of segments between the whole numbers. Since the denominator of the fraction is 6, we will create 5 equal segments between two whole numbers. Thus,
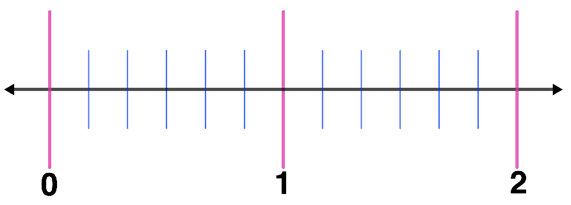
Step 4: Write the fractions on each segment. Hence,

Step 5: Shade the number line from 0 to $\frac{11}{6}$. Thus,
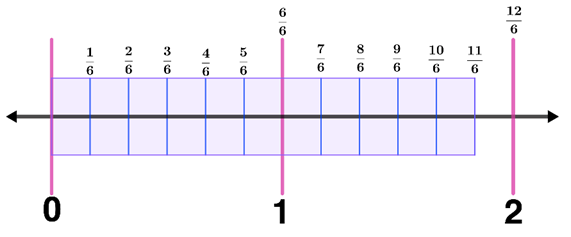
Therefore, $\frac{11}{6}$ looks like the image above when represented in a number line.
Mixed number on a number line
Like improper fractions, mixed numbers are found between 0 and any whole number when represented in a number line. To represent improper fractions on a number line, consider the following steps below:
- Draw a number line depending on the whole number of the mixed number.
- Create segments with equal distances between two whole numbers. The number of segments will depend on the denominator of the given fraction.
- Write the fractions with the denominator on the segments created.
- Write the numerator the same as writing the counting numbers.
- Shade the fractional part from 0.
Example
Represent $3\frac{1}{3}$ on a number line.
Solution
Step 1: Draw a number line from 0 to 4. This is because, $3\frac{1}{3}$ is between 3 and 4.
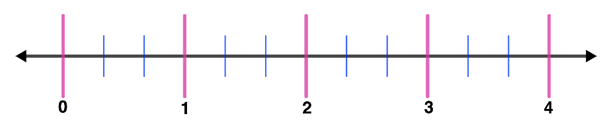
Step 2: Create segments with equal distances between two whole numbers. Since the denominator is 3, we will draw 2 equal segments between two numbers. Hence,
Step 3: Write the fractions on each segment using mixed numbers. Thus,
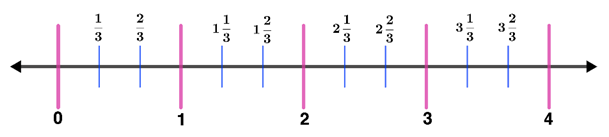
Step 4: Shade the number line from 0 to 3 .

Therefore, $3\frac{1}{3}$ looks like the image above when represented in a number line.
What is an equivalent fraction?
Two or more fractions that are all the same are called equivalent fractions. Say, for example, and . When we get the lowest term of , the result is . Hence, they are equivalent.
How to show equivalent fractions on a number line?
Equivalency in fractions can be shown on a number line just like it can be represented on an area model.
Consider the fractions $\frac{3}{4}$ and $\frac{5}{8}$ When represented using an area model, we will have:
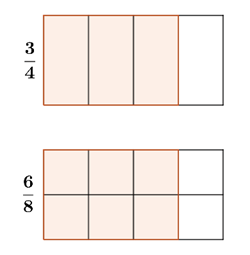
Since they are equivalent fractions, their visual models will always be the same.
Now, let’s see how we can show these equivalent fractions on a number line. First, represent $\frac{3}{4}$ on a number line. Hence,
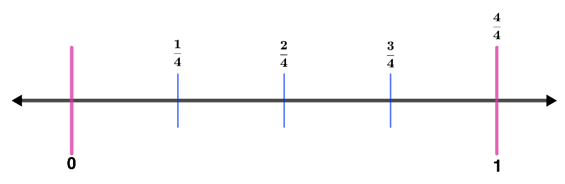
Using the same number line, represent $\frac{6}{8}$ on the number line. Thus,
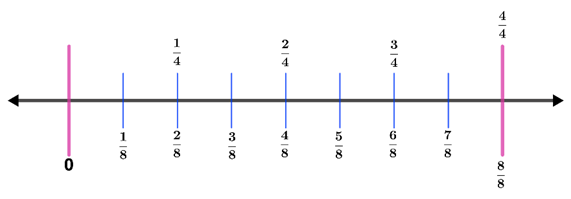
Now, let’s shade $\frac{3}{4}$ and $\frac{6}{8}$. Hence,

Therefore, we now know how and looks like when represented in the same number line.
But, how do these equivalent fractions differ from one another? Observe the number line created in step 2.

Here, we can see that the “jump” of fractions is greater if we have a denominator of 4 compared to having a denominator of 8. Hence, we can conclude that $\frac{1}{4}$ is greater than $\frac{1}{8}$. We can also note that unit fractions with a smaller denominator have greater value compared to unit fractions with a larger denominator.
Example
How can we show equivalent fractions $\frac{1}{3}$ and $\frac{2}{6}$ on a number line?
Solution
Step 1: Draw a number line from 0 to 1.

Step 2: Represent $\frac{1}{3}$ on a number line. Hence, create 2 equal segments between 0 and 1 and label the fractions.
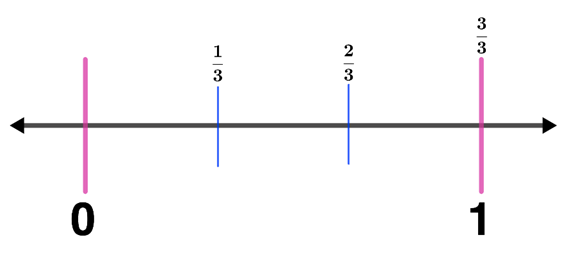
Step 3: Using the same number line in Step 2. Represent $\frac{2}{6}$ on the number line. Since the denominator is 6, we need to create 5 equal segments between 0 and 1. Thus,
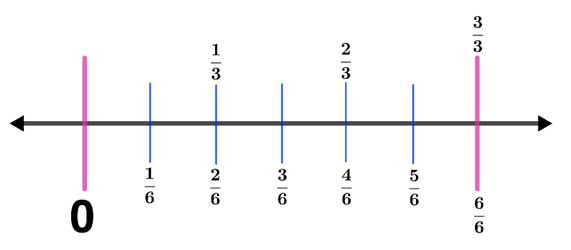
Step 4: Shade the fractions $\frac{1}{3}$ and $\frac{2}{6}$. Hence,
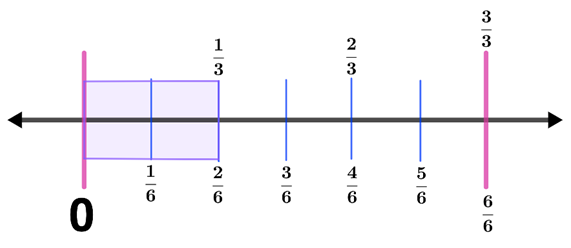
Therefore, $\frac{1}{3}$ and $\frac{2}{6}$ have the same image when represented in a number line.
What are the common misconceptions of representing fractions on a number line?
Below is the list of some common misconceptions of students when it comes to representing fractions on a number line:
- The students draw points using whole numbers rather than fractional parts. This is because they understand fractions as whole numbers.
- When given unit fractions, students tend to write fractions in ascending order based on the denominator. They conclude that a unit fraction with a greater denominator has a greater value than fractions with a smaller denominator.
- The student sees the fractions as two unrelated whole numbers separated by a line.
- Students don’t realize that the intervals must always be equal when partitioning a whole or a fraction into unit fractions.
- The student does not understand the importance of identifying the whole of a fraction.
- On the number line, the student tends to forget the significance of zero in a number line. Students can sometimes count the hash mark at zero as the first number in the sequence.
- Students tend to forget that many possibilities of fractions can be shown from 0 to 1.
- The student tends to diminish the fact that a fraction can be greater than 1.
What is the importance of knowing fractions on a number line?
Learning and understanding the concept of fractions can sometimes be hard for your child. Teaching them how to represent fractions on a number line will help them quickly see how fraction looks. Number lines assist students in comprehending the abstract concept of numbers and fractions, which is beneficial for kids with learning and thinking disabilities.
The following are some of the benefits of utilizing a number line in teaching fractions:
- Compare different fractions.
Number lines allow children to compare different fractions, which can sometimes be challenging to achieve with charts. According to studies, the ability to determine whether a fraction is larger than, less than, or equal to another fraction on a number line is the best predictor of fraction success.
- Differentiate a whole and part.
Students can easily see how many parts of a whole are divided. This is because it demonstrates that the denominator reflects the number of equal parts divided into equal parts.
- Determine equivalent fractions.
Number lines allow students to identify equivalent fractions easily. Representing equivalent fractions on a number line also helps students identify that a unit fraction with a smaller denominator has greater value than unit fractions with a larger denominator.
- Easy to visualize and make.
Compared to creating models and charts, number lines are easier to make and visualize, especially if we are asked to represent fractions between any two whole numbers. Consider a pie sliced into eight. Slicing a pie into 8 equal parts can be easy. However, students may have trouble when it comes to cutting it into 7 equal parts.
- Apply the knowledge when reading a weighing scale.
The concept of representing a number line can be seen on a manual weighing scale. Students will easily be able to read a weighing scale if they grasp the idea of how fractions are on a number line.
Worksheets and resources for fractions on a number line
Click the links below and get your children to try the worksheets that will allow them to practice and enhance their skills on fractions on a number line.
- When teaching your child to learn fractions on number lines, this fraction chart/model may come in handy — the fraction charts below visually present how fractions differ if they have different denominators.
- Number Line Generator. This interactive number line generator will help you easily make number lines.
- Printable worksheets and number lines. The number lines below are formatted for easy printing.
- Number line. This printable number comes in handy if you want your children to practice labeling and writing fractions in order in a number line.
- Number line in thirds. This worksheet will help you practice determining fractions with a denominator of 3.
Recommended Worksheets
Fractions in the Number Line (Summer Themed) Worksheets
Decimals in a Number Line (Birthday Themed) Worksheets
Addition & Subtraction of Fractions (Guy Fawkes Night Themed) Math Worksheets









