Introduction
The idea of equivalent fractions looks simple – we have to multiply the numerator and denominator by a similar factor to get another fraction that is equivalent to the origin. However, it is not a trivial case in all conditions. When teaching about the equivalence of fractions, teachers often start by adopting the procedural rules. Equivalent fractions are fractions that represent a similar value, although they give the impression of being completely Equivalent different. Let us learn about the equivalent fractions.
Definition
Equivalent fractions that represent the same amount but have different numerators and denominators.
Equivalent fractions apply to:
- compare quantities or amounts that the fractions represent
- reduce fractions to their lowest form
- add and subtract fractions
Find Equivalent Fraction
Equivalent fractions also can be determined by multiplying or dividing by the numerator and the denominator by the same number of values. When we transform equivalent fractions into their simple type, all the values will be the same. To find equivalent fractions, we multiply the numerator and denominator by the same non-zero whole number as mentioned in the definition.


$\frac{1}{4} = \frac{2}{8}$
Multiply the numerator and the denominator of a fraction by a similar number to obtain an
equivalent fraction.
For Example, $\frac{2}{12} = \frac{6}{36}$
$\frac{2 × 3}{12 × 3} = \frac{6}{36}$ ∵ Dividing and multiplying by 3
Multiply the numerator and denominator by the same number
Two fractions that are different but equivalent through definition, numerators, and denominators will be multiples of each other. We can define the equivalent fractions by multiplying the numerator and denominator of a fraction by a similar number that will produce an equivalent. The new numbers in the new fraction will be different now fractions have the same value.
For instance ,find the unknown numbers in these Equivalent Fractions :
$\frac{3}{4} = \frac{}{16} = \frac{6}{8} = \frac{15}{}$
Solution
Step 1 : Start with the first box . Identify what is given, which in this case is the two denominators. Was the first denominator multiplied or divided to get the second denominator, and by what whole number ?
$\frac{3}{4} = \frac{}{16}$
The denominator was multiplied by 4 to get 16 :
$\frac{3}{4 × 4} = \frac{}{16}$
Step 2 : Repeat the action identified in Step 1 for the remaining part
The numerator must also be multiplied by 4 :
$\frac{3 × 4}{4 × 4} = \frac{12}{16}$
Step 3 : Repeat Steps 1 and 2 to find the next missing number.
$\frac{3}{4} = \frac{12}{16} = \frac{6}{}$
The numerator was divided by 2 :
$\frac{3}{4} = \frac{12 ÷ 2}{16 ÷ 2} = \frac{6}{8}$
Step 4 : Repeat Steps 1 and 2 for the last fraction. If it is not possible to perform Step 1 with the fraction to the left of the missing number, use any other fraction that is complete.
$\frac{3}{4} = \frac{}{16} = \frac{6}{8} = \frac{15}{}$
It is not possible to multiply the numerator 6 or the numerator 12 by a whole number and then get 15 as an answer. You have to use the fraction $\frac{3}{4}$
The numerator was multiplied by 5 :
$\frac{3}{4} = \frac{3 × 5}{4} = \frac{15}{}$
The denominator must also be multiplied by 5 :
$\frac{3}{4} = \frac{3 × 5}{4 × 5} = \frac{15}{20}$
Step 5 : Write down the full answer.
$\frac{3}{4} = \frac{12}{16} = \frac{6}{8} = \frac{15}{20}$
Simplifying Equivalent Fractions
There is an easy method to finding an equivalent for any fraction. For this, We have to multiply the numerator (the number on the top or left of the line of the fraction) and denominator (the number on the bottom or right of the line) of the fraction by a similar whole number. The output will be an equivalent fraction. Let’s look at an equivalent fraction for 1/5 found by multiplying it by 5:
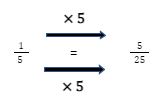
You can also find equivalent fractions by dividing the numerator and denominator of a fraction by the similar number. For example, if we divide both sides of 6/12 by 6 , we get And so, 6/12 and 1/2 are equivalent fractions.
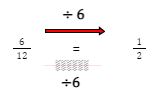
Determine Equivalent Fractions using area model
- Use the given models to complete the equivalent fraction sentence. The colored pieces in each model show parts of the whole $\frac{}{6} = \frac{1}{3}$
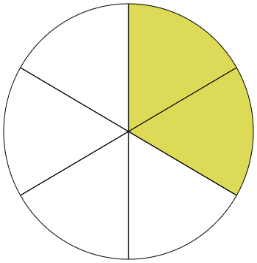

The model has 2 colored pieces out of 6 total pieces
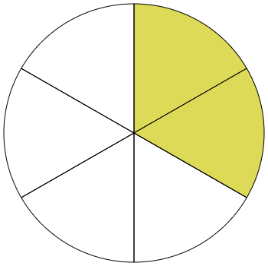
So, the fraction with a denominator of 6 is 2/6.
The other fraction is 1/3. It has a denominator of 3.
To see that the fractions are equivalent, divide the 6 total pieces into 3 groups. Each group has 2 pieces.

There is 1 colored group out of 3 total groups.
This is the completed equivalent fraction sentence:
$\frac{2}{6} = \frac{1}{3}$
• Use the given models to complete the equivalent fraction sentence. The colored pieces in each model show parts of the whole $\frac{4}{} = \frac{2}{6}$
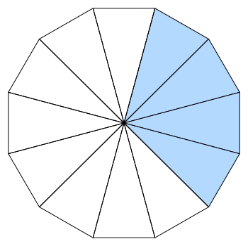
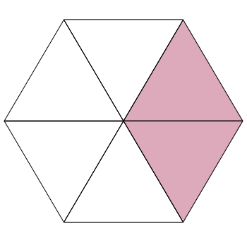
The model has 4 colored pieces out of 12 total pieces.
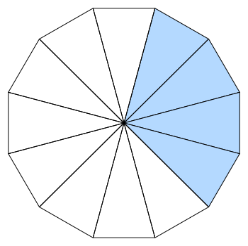
So, the fraction with a denominator of 12 is $\frac{4}{12}$ .
The other fraction is $\frac{2}{6}$. It has a denominator of 6.
To see that the fractions are equivalent, divide the 12 total pieces into 6 groups. Each group has 2 pieces.
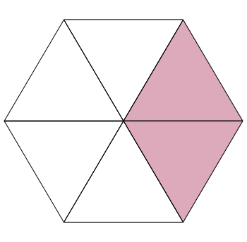
There is 2 colored group out of 6 total groups.
This is the completed equivalent fraction sentence
$\frac{4}{12} = \frac{2}{6}$.
Equivalent Fractions on number line
We have already learned to determine equivalent fractions using area models. We will talk about equivalent fractions and how using a number line can help us find the equivalent fractions. Equivalent fractions are different ways to write similar fractions. We know that the equivalent fractions are at the same place on a number line according to given points.
For example, is $\frac{2}{4}$ and is $\frac{1}{2}$ are equivalent fractions. If you simplify is $\frac{2}{4}$ by dividing both the numerator and denominator by 2, you’ll get is $\frac{1}{2}$, the same as the other one:
We know that our number line is a line with equally spaced tick marks that show us our numbers. First, we need to locate our fraction on the number line. For this, we need to divide the first tick mark into even pieces. For fraction First, we need to locate our fraction on the number line. For this, we need to divide the first tick mark into even pieces. For fraction is $\frac{1}{2}$. We will divide the first tick mark (the space between the numbers 0 and 1) into two even pieces. For fraction is $\frac{1}{3}$, we divide the first tick mark into three parts(even). So, the denominator tells us how many (even) pieces to divide that first tick mark into, and the numerator tells you which of those tick marks our fraction is. Place a small tick mark on our dividers.

So, $\frac{1}{2}$ has we divide in our first tick mark into two even spaces. We place a small tick mark in the middle of our line between the number 0 and the number 1. The numerator 1 tells us that our fraction is the first of the small tick marks.

Next to find equivalent fractions, we divide the divisions that we made from step 1 into two even spaces and for fraction $\frac{2}{4}$, we will divide the two divisions we made in step 1 in half. So we will have four equal spaces between our number 0 and 1 now.

To determine the equivalent fraction is, we’ll now need to read our number line. For our $\frac{1}{2}$, we remember that the $\frac{1}{2}$ is the middle separation between the number 0 and the number 1. But for this number line, we now have four separations. So, this means the denominator is now 4. The middle line between 0 and 1 is the second small tick mark, so the numerator is 2.
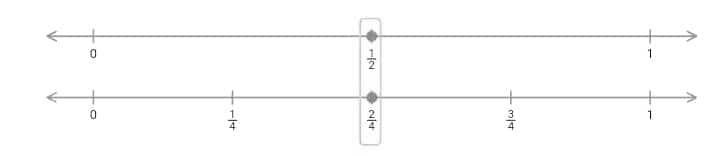
Both number lines show numbers between 0 and 1. Equivalent fractions are at the same place between 0 and 1 on the number line. Look for a pair of equivalent fractions. This means that $\frac{1}{2}$ and $\frac{2}{4}$ are equivalent fractions.
Equivalent Fractions using LCM
Lowest Common Multiples (LCM) can be used to find a common denominator when adding and subtracting fractions and mixed number in fractions. To find equivalent fractions of two or more fractions, list multiples of each denominator. Identify the smallest (lowest) multiple that is present in both fractions. In the process when we are finding equivalent fractions then we multiply or divide the numerator and denominator in the fraction by the same number.
For example, Find the equivalent fractions of $\frac{3}{5}$ and $\frac{9}{15}$ using 15 LCM as the denominator
$\frac{3}{5} = \frac{}{15}$
Solution :
What number multiplied by 5 equals 15? The number is 3. Multiply the numerator 3 by 3 =9.
$\frac{3 × 3}{5 × 3} = \frac{9}{15}$
$\frac{3}{5} = \frac{9}{15}$
$\frac{9}{15} = \frac{}{15}$
What number multiplied by 15 equals 15? The number is 1. Multiply the numerator 9 by 1 =9.
$\frac{9 × 1}{15 × 1} = \frac{9}{15}$
We have showed that $\frac{3}{5}$ and $\frac{9}{15}$ are equivalent fractions with LCM 15.
We have another example of Equivalent Fractions with LCM,
Find the Equivalent Fractions of $\frac{1}{6}$ and $\frac{5}{4}$ using 12 LCM as the denominator
$\frac{1}{6} = \frac{}{12}$
What number multiplied by 6 equals 12? The number is 2. Multiply the numerator 1 by 2 =2.
$\frac{1 × 2}{6 × 2} = \frac{2}{12}$
$\frac{1}{6} = \frac{2}{12}$
Now $\frac{5}{4} = \frac{}{12}$
What number multiplied by 4 equals 12? The number is 3. Multiply the numerator 5 by 3 =15.
$\frac{5× 3}{4 × 3} = \frac{15}{12}$
$\frac{5}{4} = \frac{15}{12}$
We have showed that $\frac{1}{6}$ and $\frac{2}{12}$ also $\frac{5}{4}$ and $\frac{2}{12}$ are equivalent fractions with LCM 12.
Lowest form of Equivalent Fractions
The fraction that has numerator and denominator of a fraction in lowest terms having no common factors except one is called lowest form of equivalent fraction. A fraction can be reduced by dividing fractions from both the numerator and denominator by the similar nonzero whole number.
We can imagine that each of the last four fractions can be converted into reduced to the first. Now $\frac{1}{4}$ fractions by dividing both the numerator and denominator by, respectively, 2, 3, 4, and 5. When a fraction is reduced to the fraction that has the smallest numerator and denominator in its collection of equivalent fractions, it is said to be reduced to lowest terms.
The fractions $\frac{1}{4}, \frac{3}{8}$ and $\frac{2}{5}$ are all reduced to lowest terms.
The whole number that divides fractions from both the numerator and denominator without a remainder is the number 1. When 1 is the only whole number present in fraction that divides two whole numbers in fractions , these two whole numbers are considered to be relatively prime which is also called the definition of prime Numbers.
Relatively Prime
A fraction is converted into reduced or lowest forms if its numerator and denominator are relatively prime to each other. We can use different methods of converting fractions into Reducing Fractions to Lowest Terms.
Dividing Out Common Primes
In the process of dividing out common prime numbers for getting the equivalent fractions. First, we will divide the numerator and denominator by each of the common prime factors as prime factorization. Secondly, we will get after cancellation from the fraction then we have remaining factors in the numerator and the product of remaining factors of the denominator are relatively prime to each other, and this fraction now is converted into reduced to lowest terms of equivalent fractions.
For example
$\frac{6}{12} = \frac{2 × 3}{2 × 2 × 3} = 1$
Where are 1 and 2 are relatively coprime to each other We can see another example also:
If we have
$\frac{6}{12} = \frac{2 × 3}{5 × 3} = \frac{2}{5}$
Where 2 and 5 are coprime to each other.
In both examples we have been that we have equivalent fractions $\frac{6}{12}$ and $\frac{1}{2}$ also $\frac{6}{15}$ and $\frac{2}{5}$.
Raising Fractions power to Higher Terms
By increasing a fraction to higher order terms is the process of making an equivalent fraction in which we increase the values in the numerator and denominator than the given fraction.
The fraction $\frac{3}{4}$ can be raised to $\frac{27}{36}$ by multiplying both the numerator and denominator by 9.
$\frac{3}{4} = \frac{3 × 9}{4 × 9} = \frac{27}{36}$
Note that here $\frac{9}{9}$ =1.
Mostly, we convert a given fraction to an equivalent fraction with a increased specified denominator.
Suppose we have fractions $\frac{3}{4}$ and we want an equivalent fractions by that has denominator 24.
$\frac{3}{4} = \frac{}{24}$
This is simple to do because we know the process. We must multiply both the numerator and denominator of $\frac{3}{4}$ by same none zero whole number in order to 4 obtain an equivalent fraction.
We know that
24÷4=6
Now, multiply the numerator 3 with 6
3×6=18
We have
$\frac{3}{4} = \frac{3 × 6}{4 × 6} = \frac{18}{24}$
So ,
$\frac{3}{4} = \frac{18}{24}$ ,both are equivalent fractions.
Equivalent Fraction charts
Let us see the equivalent fractions of odd Numbers unit fractions.
| Unit Fraction | Equivalent Fractions |
| 1/3 | 2/6,3/9,4/12,5/15,6/18,… |
| 1/5 | 2/10,3/15,4/20,5/25,6/30,… |
| 1/7 | 2/14,3/21,4/28,5/35,6/42,… |
| 1/9 | 2/18,3/27,4/36,5/45,6/54,… |
| 1/11 | 2/22,3/33,4/44,5/55,6/66,… |
| 1/13 | 2/26,3/39,4/52,5/65,6/78,… |
| 1/15 | 2/30,3/45,4/60,5/75,6/90,… |
Solved Examples:
Example 1 :
Consider the shaded areas in these rectangles, where
We have
$\frac{3}{5}$ $\frac{12}{20}$
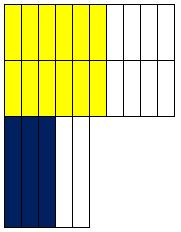
Show that these two these rectangles with given fractions are equivalent?
Solution :
We can see easily
$\frac{12}{20} = \frac{3 × 4}{5 × 4} = \frac{3}{5} and \frac{3}{5} = \frac{3 × 4}{5 × 4} = \frac{12}{20}$
Both given $\frac{3}{5}$ and $\frac{12}{20}$ are equivalent fraction .
Example 2 :
Are $\frac{16}{20}$ and $\frac{4}{5}$ are equivalent fraction ?
Solution :
We will see first
$\frac{16}{20} = \frac{4 × 4}{5 × 4} = \frac{4}{5} and \frac{4}{5} = \frac{4 × 4}{5 × 4} = \frac{16}{20}$
So, from above calculation it is clear that $\frac{16}{20}$ and $\frac{4}{5}$ are equivalent fraction .
Example 3 : Ryan makes a circle. He divides the circle into 4 sections. He filled $\frac{1}{4}$ section of the circle. As shown below,

Emily makes a circle . She divides the circle into 8 sections. She filled $\frac{2}{8}$ section of the circle. As shown below.
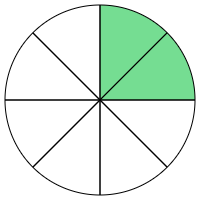
Show that these circle’s are equivalent fractions?
Solution :
The shaded area of both diagrams remain the same.
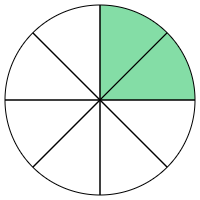

Area 1/4 = Area 2/8
These are known as Equivalent Fractions.
Example 4 :
We have two rectangles. The area of ( fig 1) is filled 6/16
and the area of (fig 2 ) is shaded 3/8 as shown below.
Show that these two rectangles are equivalent fractions?

Fig 1.
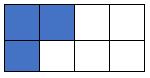
Fig 2.
Solution :
From fig 2 , we can see that the area of (fig 2 ) is shaded $\frac{3}{8}$
$\frac{3}{8} = \frac{3× 2}{8 × 2}$ Multiplying nominator and denominator by 2.
$\frac{3}{8} = \frac{6}{16}$
From calculation we see that these are Equivalent Fractions.
$\frac{3}{8} = \frac{6}{16}$
Since , both two rectangles are equivalent fractions.
Example 5 :
Consider a mixed fraction 1$\frac{1}{3}$. Transform into Equivalent fraction ?
Solution :
1$\frac{1}{3} = \frac{( 1 × 3 + 1 )}{3} = \frac{4}{3}$
The equivalent fractions for $\frac{4}{3}$ are
$\frac{4}{3} = \frac{4 × 4}{3 × 4}$ dividing and multiplying with 4.
$\frac{4}{3} = \frac{16}{12}$.
We can see that fraction 1$\frac{1}{3}, \frac{4}{3} and \frac{16}{12}$ are equivalent fractions.
Note :
For generalize case :
When we multiply the nominator and divide the denominator with n-elements
n = 5 , 6 , 8 , . . . . . .
then we get n- equivalent fractions for given elements
like we can see the case for n = 5 ,it means we will multiply the nominator and divide the denominator with 5
$\frac{4}{3} = \frac{4 ×5}{3 ×5}$ dividing and multiplying with 5
$\frac{4}{3} = \frac{20}{15}$
We can see that fraction 1$\frac{1}{3}, \frac{4}{3}, \frac{16}{12}$ and $\frac{20}{15}$ are equivalent fractions and it is true for n- elements.
Example 6 :
Different Equivalent Fractions are
1) $\frac{7}{9}$ and $\frac{42}{54}$ are equivalent fractions
2) $\frac{1}{4}$ and $\frac{23}{92}$ are equivalent fractions
3) $\frac{1}{18}$ and $\frac{15}{270}$ are equivalent fractions
4) $\frac{1}{117}$ and $\frac{8}{936}$ are equivalent fractions
We can easily solve these equivalent fractions:
Solutions :
$\frac{7}{9} = \frac{7×6}{9×6} = \frac{42}{54}$ (By multiplying the nominators and dividing the denominator with 6 )
So, $\frac{7}{9}$ and $\frac{42}{54}$ are equivalent fractions.
$\frac{1}{4} = \frac{1 × 23}{4 × 23} = \frac{23}{92}$ (By multiplying the nominators and dividing the denominator with 23 )
So, $\frac{1}{4}$ and $\frac{23}{92}$ are equivalent fractions.
$\frac{1}{18} = \frac{1 × 15}{18 × 15} = \frac{15}{270}$ (By multiplying the nominators and dividing the denominator with 15 )
So, $\frac{1}{18}$ and $\frac{15}{270}$ are equivalent fractions.
$\frac{1}{117} = \frac{1 × 8}{117× 8} = \frac{8}{936}$ ( By multiplying the nominators and dividing the denominator with 8 )
So, $\frac{1}{117}$ and $\frac{8}{936}$ are equivalent fractions.
Example 7 :
Key facts and Summary
- Equivalent fractions denote the same amount of distance on a number line.
- All equivalent fractions reduce to the similar fraction in their simplest form.
- Equivalent fractions are fractions with different denominators that have the similar meaning.
- A fraction is considered simplified or Lowest reduced form if there are no common factors in the numerator and denominator.
- If a, b, and c are numbers where b ≠ 0, c ≠ 0,then we have $\frac{a}{b} = \frac{a.c}{b.c}$ and $\frac{a.c}{b.c} = \frac{a}{b}$.
- By rearranging the numerator and the denominator to show their common factors into prime numbers.
- Simplify using the property of the equivalent fractions by excluding the common factors.
- You can obtain an equivalent fraction by multiplying or dividing the top and bottom sides by the same value.
- You can only multiply or divide the fractions, never add or subtract the fractions, to obtain an equivalent fraction.
- Only divide when the top and bottom remain as whole numbers.
Recommended Worksheets
Equivalent Fractions (Ages 7-9) Worksheets (Snacks themed)
Illustrating Equivalent Fractions Using Fraction Model (with denominators 8, 10, 12, 100) 4th Grade Math Worksheets
Illustrating Equivalent Fractions Using Fraction Models 4th Grade Math Worksheets









