Addition And Subtraction Of Proper Fractions

Introduction

We have learnt that a fraction is a number representing a part of a whole. The whole may be a single or a group of objects. Let us now learn about the addition and subtraction of proper fractions.

Fraction in its Simplest Form

It is also important to recall that a fraction is said to be in the standard form if the denominator is positive and the numerators have no common divisor other than 1.

In order to express a given fraction in the standard form, the following steps should be followed –

Step 1 – Check whether the given number is in the form of a fraction.

Step 2 – See whether the denominator of the fraction is positive or not. If it is negative, multiply or divide the numerator as well as the denominator by -1 so that the denominator becomes positive.

Step 3 – Find the greatest common divisor (GCD) of the absolute values of the numerator and the denominator.

Step 4 – Divide the numerator and the denominator of the given fraction by the GCD (HCF) obtained in step III. The fraction so obtained is the standard form of the given fraction.

This was important to understand because, after the addition or subtraction of fractions, we will need to reduce them in the simplest form.

Now, let us learn how to add two or more proper fractions. But before that let us recall what we mean by proper fractions

Proper Fractions

Fractions with the numerator less than the denominator are called proper fractions. For example, consider the fractions $\frac{1}{2} and \frac{2}{3}$. In both these fractions, the numerators less than their respective denominators. Hence they are proper fractions. However, note that the fraction $\frac{3}{3}$ is not a proper fraction as in this case the numerator is equal to the denominator. So, we can say the condition for a fraction to be an proper fraction is that its numerator should be strictly less than its denominator. Let us now understand how to add or subtract proper fractions.

Addition of Proper Fractions

Addition of Proper Fractions is done based on the equivalence of their denominators, i.e. whether they have same different denominators. Let us discuss both the cases.

Proper Fractions with Same Denominators

Recall that, fractions with the same denominator are called like fractions. Therefore, if the denominators of the proper fractions are the same, then would be called like fractions. Therefore, in order to add two proper fractions, we follow the following steps:

Obtain the numerators of the two given proper fractions and their common denominator
Add the numerators obtained in the first step.
Write a fraction whose numerator is the sum obtained in the second step and the denominator is the common denominator of the given fractions.

Let us understand it by an example.

Example

Suppose we want to add the fractions $\frac{2}{9} and \frac{5}{9}$

Solution

Here we can see that both the fractions have the same denominator, i.e. 9 and for both the fractions, the numerators as less than the denominators, which means they are proper fractions.

Therefore, we go by the above-defined steps.

We check the numerators of both the fractions. They are 2 and 5

Then, we add these numerators and get 2 + 5 = 7.

Now, we write the sum of these fractions as $\frac{7}{9}$

Hence, $\frac{2}{9} + \frac{5}{9} = \frac{7}{9}$

In the above example we have seen how to add two proper fractions having the same denominator. What if their denominators are different?

Proper Fractions with Different Denominators

Proper fractions having different denominators are called unlike fractions. . For example, $\frac{1}{7} and \frac{3}{8}$ are unlike fractions as both the fractions have different denominators. But they are proper functions as well as their numerators are less than their respective denominators.

Let us see how to add these proper fractions. We shall use the following steps to find the sum of proper fractions with different denominators.

Obtain the fractions and their denominators. The denominators of the fractions should be such that they are not the same.

Find the Least Common Multiple ( L.C.M) of the denominators. In other words, make the denominators the same by finding the Least Common Multiple (LCM) of their denominators. This step is exactly the same as finding the Least Common Denominator (LCD).

Convert each function into an equivalent fraction having the same denominator equal to the L.C.M obtained in the previous step. This means that you need to rewrite each fraction into its equivalent fraction with a denominator that is equal to the Least Common Multiple that you found in the previous step.

Since the fractions are now like fractions, add them as we do for like a fraction, i.e. add their numerators.

Reduce the fraction to its simplest form, if required.

Let us understand the above steps through an example.

Example

Add $\frac{5}{8} and \frac{3}{7}$

Solution

We have been given the fractions, $\frac{5}{8} and \frac{3}{7}$. We can clearly see that the denominators of these fractions are different, hence they are unlike fractions. Therefore, we will proceed according to the steps defined above to obtain their sum.

Let us first find the L.C.M of 8 and 7.

The L.C.M of 8 and 7 = 56

So, we will convert the given fractions into equivalent fractions with denominator 56.

We will get,

$\frac{5}{8} = \frac{5 x 7}{8 x 7} = \frac{35}{56}$

Similarly,

$\frac{3}{7} = \frac{3 x 8}{7 x 8} = \frac{24}{56}$

Now, we two fractions, $\frac{35}{56} and \frac{24}{56}$ which have a common denominator 56 and are thus like fractions. So, we will add their numerators to get,

$\frac{35}{56} + \frac{24}{56} = \frac{59}{56}$

Hence,

$\frac{5}{8} + \frac{3}{7} = \frac{59}{56}$

Note that the above fraction is an improper fraction. Therefore, we shall convert into mixed fraction to get, $1\frac{3}{56}$

Hence,

$\frac{5}{8} + \frac{3}{7} = \frac{59}{56}$

=$1\frac{3}{56}$

Subtraction of Proper Fractions

Subtraction of proper fractions, is similar to the addition of proper Fractions where the calculations are based on the equivalence of their denominators, i.e. whether they have same different denominators. Let us discuss both the cases.

Proper Fractions with Same Denominators

Obtain the numerators of the two given fractions and their common denominator
Find the difference in numerators obtained in the first step. It is important to check which numerator is the subtrahend and which one is minuend as we know that in case of subtraction a – b might not always be equal to b – a.
Write a fraction whose numerator is the difference of the sum obtained in the second step and the denominator is the common denominator of the given fractions.

Let us understand it by an example.

Example

Suppose we want to find the difference between fractions $\frac{9}{4} and \frac{5}{4}$

Solution

Here we can see that both the fractions have the same denominator, i.e. 4.

Therefore, we go by the above-defined steps.

We check the numerators of both the fractions. They are 9 and 5.

Then, we subtract 5 from 9, we will get 9 – 5 = 4

Now, we write the difference of these fractions as $\frac{4}{3}$

Hence, $\frac{9}{4} – \frac{5}{4} = \frac{4}{3}$

Let us now understand how to find the difference between proper fractions having different denominators.

Proper Fractions with Different Denominators

Again, recall that, fractions with the same denominator are called like fractions. Therefore, if the denominators of the proper fractions are the same, then would be called like fractions. Therefore, in order to add two proper fractions, we follow the following steps:

Obtain the fractions and their denominators. The denominators of the fractions should be such that they are not the same.
Find the Least Common Multiple ( L.C.M) of the denominators. In other words, make the denominators the same by finding the Least Common Multiple (LCM) of their denominators. This step is exactly the same as finding the Least Common Denominator (LCD).
Convert each function into an equivalent fraction having the same denominator equal to the L.C.M obtained in the previous step. This means that you need to rewrite each fraction into its equivalent fraction with a denominator that is equal to the Least Common Multiple that you found in the previous step.
Since the fractions are now like fractions, subtract them as we do for a like fraction, i.e. subtract their numerators.
Reduce the fraction to its simplest form, if required.

Let us understand the above steps through an example.

Example

Subtract $\frac{3}{4} from \frac{5}{6}$

Solution

We have been given the fractions $\frac{3}{4} and \frac{5}{6}$ and we are required to find the value of $\frac{5}{6} – \frac{3}{4}$

Therefore,

To find the value of $\frac{5}{6} – \frac{3}{4}$

We can clearly see that the denominators of these fractions are different, hence they are unlike fractions. Therefore, we will proceed according to the steps defined above to obtain their difference.

We will first find the L.C.M of 4 and 6

LCM of 6 and 4 is 12.

So, we will convert the given fractions into equivalent fractions with denominator 12.

Therefore

$\frac{5}{6} = \frac{5 x 2}{6 x 2} = \frac{10}{12}$ and

$\frac{3}{4} = \frac{3 x 3}{4 x 3} = \frac{9}{12}$

Now, we two fractions, $\frac{10}{12}$ and $\frac{9}{12}$ which have a common denominator 12 and are thus like fractions. So, we will subtract their numerators to get,

Therefore,

$\frac{5}{6} – \frac{3}{4} = \frac{10}{12} – \frac{9}{12} = \frac{10-9}{12} = \frac{1}{12}$

Hence, $\frac{5}{6} – \frac{3}{4} = \frac{1}{12}$

Graphical representation of Addition of Proper Fractions

Before proceeding with the graphical representation of the addition of proper fractions, we must recall what we mean by the graphical representation of a fraction. Let us consider the fraction $\frac{3}{4}$ . This fraction is read as “three-fourth” which means three parts out of four equal parts in which a whole has been divided. Graphically, this fraction can be represented as –

Now, that we recalled how to graphically represent a fraction, let us move ahead with our discussion on the graphical representation of the addition of proper fractions. We will understand it by an example.

Suppose we have the fractions, $\frac{2}{8}, \frac{3}{8} and \frac{1}{8}$ and we want to add these fractions. If we go by the steps that we have defined above for the addition of proper fractions, we can see that all the three fractions have the same denominator, i.e. 8. So, in order to add these fractions, we will simply add their numerators, i.e. 2, 3 and 1. We will get 2 + 3 + 1 = 6. Therefore,

$\frac{2}{8} + \frac{3}{8} + \frac{1}{8} = \frac{6}{8}$

Now, let us represent each of these fractions, graphically.

The fraction $\frac{2}{8}$ will graphically be represented as

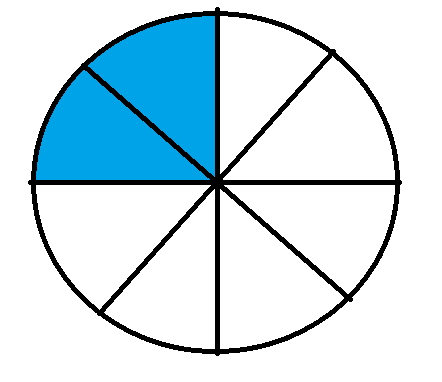
We can see that the above fraction has 2 shaded parts out of a total of 8 equal parts.

The fraction $\frac{3}{8}$ will graphically be represented as

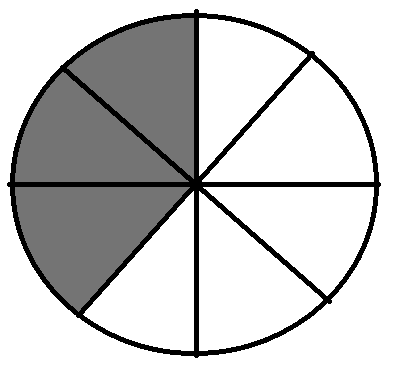
We can see that the above fraction has 3 shaded parts out of a total of 8 equal parts.

The fraction $\frac{1}{8}$ will graphically be represented as

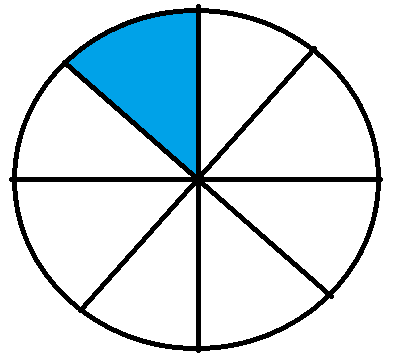
We can see that the above fraction has 1 shaded part out of a total of 8 equal parts.

If we sum up all the shaded parts in the three fractions, we can see that we will have 2 + 3 + 1 = 6 shaded parts. This will be represented graphically as –

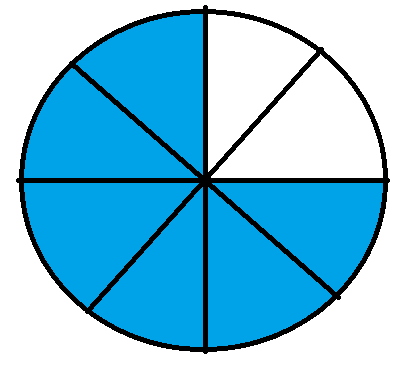
The above fraction will be written as $\frac{6}{8}$ which is the result that we had obtained after we added the three fractions above.

Now, that we have understood how to add proper fractions both using steps as well as graphically, let us learn how to find the difference of two or more proper fractions.

Graphical representation of Subtraction of Proper Fractions

Suppose we have the fractions, $\frac{5}{8}$ and $\frac{1}{8}$ and we want to find the difference between these fractions. If we go by the steps that we have defined above for subtraction of proper fractions, we can see that the two fractions have the same denominator, i.e. 8. So, in order to subtract these fractions, we will simply subtract the numerators, i.e. 5 and 1. We will get 5 – 1 = 4 Therefore,

$\frac{5}{8} – \frac{1}{8} = \frac{4}{8}$

Now, let us represent each of these fractions, graphically.

The fraction $\frac{5}{8}$ will graphically be represented as

We can see that the above fraction has 5 shaded parts out of a total of 8 equal parts.

The fraction $\frac{1}{8}$ will graphically be represented as

We can see that the above fraction has 1 shaded part out of a total of 8 equal parts.

If we subtract the two shaded parts in these fractions, we can see that we will have 5 – 1 = 4 shaded parts. This will be represented graphically as –

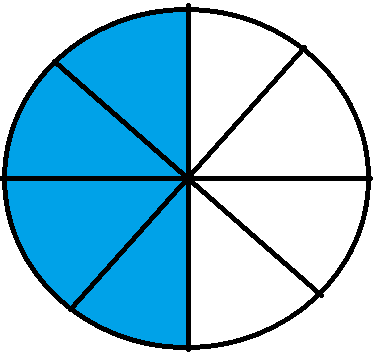
The above fraction will be written as $\frac{4}{8}$ which is the result that we had obtained after we subtracted the two proper fractions above.

Solved Examples

Example 1 Sam bought $\frac{5}{9}$ kg pasta whereas Peter bought $\frac{2}{3}$ kg of pasta. Find the total amount of pasta bought by both of them.

Solution We have been given that Sam bought $\frac{5}{9}$kg of pasta whereas Peter $\frac{2}{3}$kg of pasta. We are required to find the total amount of pasta bought by both of them.

To find the answer to the above problem, let us first understand the fraction values given to us.

Pasta bought by Sam = $\frac{5}{9}$kg

Pasta bought by Peter = $\frac{2}{3}$kg

It can be clearly seen that both the fractional values have the same denominator, i,e 3. Therefore the first thing to be noticed is that they are unlike fractions. So we will have to first find the L.C.M. of the denominators to convert them into equivalent fractions.

L.C.M of 3 and 9 is 9

Therefore,

Note, that the fraction $\frac{5}{9}$ already has the denominator as 9, so we need not convert it any further.

$\frac{2}{3}= \frac{2 x 3}{3 x 3} = \frac{6}{9}$

Now, to find the value of the total pasta bought by them, we will need to add the two fractions. We shall proceed with adding these fractions by adding the numerators as we have learnt above.

So the total pasta bought by both of them = Pasta bought by Sam + Pasta bought by Peter

Now, adding their numerators we have, 5 + 6 = 11

Therefore, $\frac{5}{9}kg + \frac{2}{3}kg = \frac{11}{9}$kg

Hence, Amy and Patricia together bought $\frac{11}{9}$kg of pasta.

Example 2 The sum of two fractions is $\frac{-3}{5}$. If one of the numbers is $\frac{-9}{20}$, find the other.

Solution We have been given that the sum of two fractions is $\frac{-3}{5}$ and one of the numbers is $\frac{-9}{20}$.

Let the other number be “p”.

Therefore,

p + $\frac{-9}{20}$= $\frac{-3}{5}$

⇒ p = $\frac{-3}{5}$ – ($\frac{-9}{20}$)

⇒ p = $\frac{-3}{5}$ + $\frac{9}{20}$

⇒ p = $\frac{(-3)x 4 + (9 x 1)}{20}$

⇒ p = $\frac{-12+9}{20}$

⇒ p = $\frac{-3}{20}$

Hence, the other number is $\frac{-3}{20}$

Key Facts and Summary

A fraction is a number representing a part of a whole. The whole may be a single or a group of objects.
A fraction is said to be in the standard form if the denominator is positive and the numerators have no common divisor other than 1.
To reduce a fraction to its simplest form Find the greatest common divisor (GCD) of the absolute values of the numerator and the denominator. Divide the numerator and the denominator of the given fraction by the GCD (HCF) obtained in step III. The fraction so obtained is the standard form of the given fraction.
The number that is subtracted is called the subtrahend while the number from which the subtrahend is subtracted is called minuend. The result of this subtraction is called the difference.
Fractions with the numerator strictly less than the denominator are called proper fractions.
Fractions with the same denominator are called like fractions while fractions with different denominators are called unlike fractions.
In order to add two or more proper fractions with the same denominators, we add the fractions in the same manner as we do for like fractions.
In order to add two or more proper fractions with different denominators, we first convert them into the corresponding equivalent like fractions and then they are added in the same manner as we do for like fractions.

Recommended Worksheets

Subtraction of Proper Fractions (Olympic Games Themed) Worksheets
Addition of Proper Fractions (Ages 9-10) Worksheets (Election Day Themed)
Multiplication of Proper Fractions (Veterans Day Themed) Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!