Dividing Whole Numbers by Fractions | Examples, How & Model

Introduction

When dividing whole numbers by fractions, what should we do?

When a whole number is divided by a fraction, the number of groups of the fraction that fit inside the whole is determined. Multiplying the given whole number by the reciprocal fraction is the most popular way to divide whole numbers by fractions.

We will learn more about dividing whole numbers by fractions in this article and the different ways of doing it.

What is meant by dividing whole numbers by fractions?

Definition

When a whole number is divided by a fraction, the number of groups of the fraction that fit inside the whole is determined.

Let us first look at dividing whole numbers. Let us say 6 ÷ 3. We want to find out how many threes makeup six. The figure below illustrates 6 ÷ 3 = 2. We can say that if we divide 6 by 3, there will be 2 equal groups of 3.

The division of whole numbers by fractions works the same way since we also want to identify how many equal groups of the fraction fit in the given whole number.

Let us say, for example, we want to calculate 6 ÷ ¾. Here, we want to identify how many ¾ fit the whole number 6. Using a visual model or a diagram, let us look at how we divide 6 by ¾.

Let us use 6 squares, and since the denominator of ¾ is 4, we shall divide each square by 4. Hence, we have,

Now, since we are dividing the whole number by the fraction ¾, we will create groups with 3 squares. The figure below shows the different colors of each group with three squares.

Notice that each square has one leftover part that remains unshaded. We can still form groups using three squares. The number of equal groups is the answer to the division problem.
Therefore, 6 ÷ ¾ = 8.

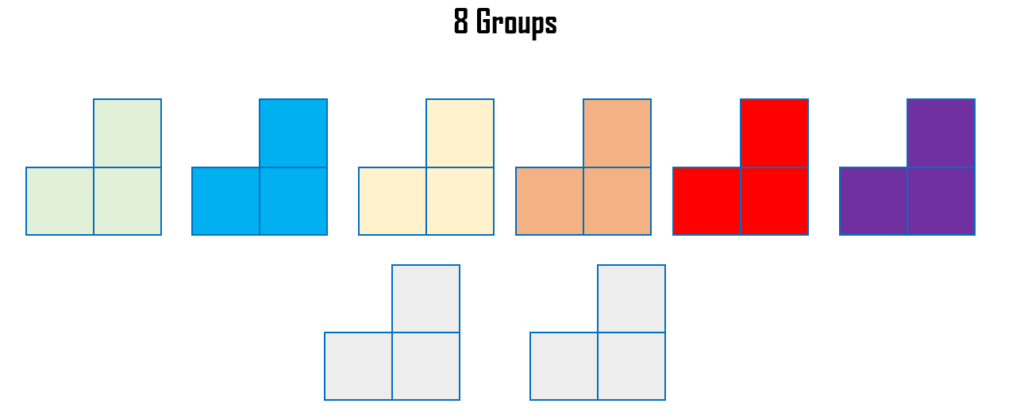
Dividing Whole Numbers by Fractions Using Visual Model

The number of groups of the fraction that fit inside the whole is found when a whole number is divided by a fraction. When dividing whole numbers by fractions using diagrams, we first draw shapes to represent whole numbers and divide each shape in reference to the fraction’s denominator.

For example, we want to calculate 5÷²⁄₃; the figure below shows five squares since it is the given whole number, and each square is divided into 3 equal parts in reference to the fraction’s denominator. To represent the fraction ²⁄₃, 2 parts are shaded in each square.

We will then count the number of groups of ²⁄₃. Notice that we have formed 7 groups and 1 piece as a leftover.

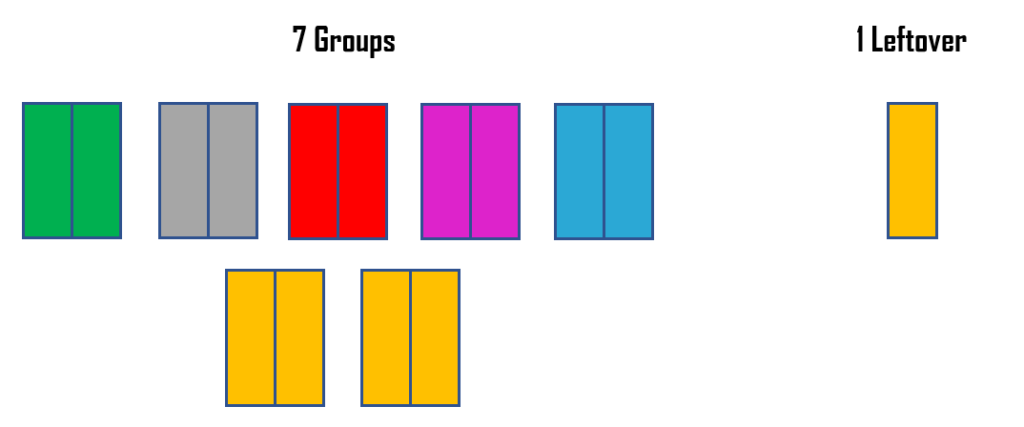
The 7 groups will give the whole number answer to the division problem, but the leftover piece must be interpreted and compared over to a complete group. In the illustration above, each group has 2 parts. The 1 piece will then be interpreted as ¹⁄₂. Combining the whole number answer and the fractional number gives us 7 ¹⁄₂.

Therefore, 5 ÷ ²⁄₃ = 7 ¹⁄₂.

How to Divide Whole Numbers by Fractions?

The processes of dividing whole numbers by fractions are as follows:

Step 1: Keep the same whole number.
Step 2: Change the division symbol into the multiplication symbol.
Step 3: Flip the fraction.
Step 4: Multiply the whole number by the flipped fraction.
Step 5: Simply, if necessary.

Example 1

Calculate 4 ÷ ¹⁄₂.

Solution

Let us follow the steps of dividing whole numbers by fractions.

Step 1: We will keep the same whole number, 6.
Step 2: Change the division symbol into the multiplication symbol.
Step 3: Flip the fraction.
Since the given fraction is ½, it becomes 2/1.
Step 4: Multiply the whole number by the flipped fraction.
Multiply 4 by 2, then divide the answer by 1.
4 × $\frac{2}{1}$ = $\frac{8}{1}$
Step 5: Simply, if necessary.

$\frac{8}{1}$ is equal to 8 when simplified.

Example 2

Calculate 5 ÷ ³⁄₄.

Solution

Let us follow the steps of dividing whole numbers by fractions.

Step 1: We will keep the same whole number, 5.
Step 2: Change the division symbol into the multiplication symbol.
Step 3: Flip the fraction.
Since the given fraction is ¾, it becomes $\frac{4}{3}$.
Step 4: Multiply the whole number by the flipped fraction.
Multiply 5 by 4, then divide the answer by 3.
5 × $\frac{4}{3}$ = $\frac{20}{3}$
Step 5: Simply, if necessary.

$\frac{20}{3}$ is equal to 6$\frac{2}{3}$ when simplified or as a mixed fraction.

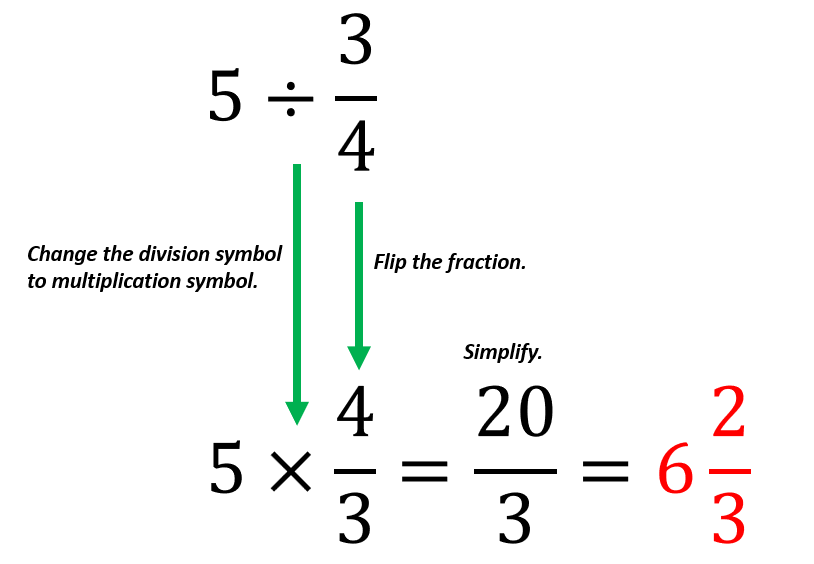
Example 3

Solve 12 ÷ $\frac{4}{7}$.

Solution

Let us follow the steps of dividing whole numbers by fractions.

Step 1: We will keep the same whole number, 12.
Step 2: Change the division symbol into the multiplication symbol.
Step 3: Flip the fraction.
Since the given fraction is $\frac{4}{7}$, it becomes $\frac{7}{4}$.
Step 4: Multiply the whole number by the flipped fraction.
Multiply 12 by 7, then divide the answer by 4.
12 × $\frac{7}{4}$ = $\frac{84}{4}$
Step 5: Simply, if necessary.

$\frac{84}{4}$ is equal to 21 when simplified.

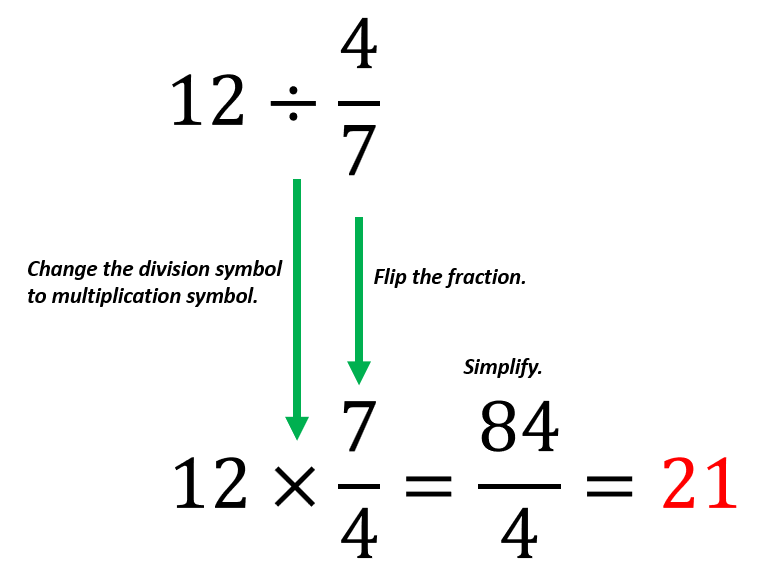
Example 4

Solve 13 ÷ $\frac{5}{6}$.

Solution

Let us follow the steps of dividing whole numbers by fractions.

Step 1: We will keep the same whole number, 13.
Step 2: Change the division symbol into the multiplication symbol.
Step 3: Flip the fraction.
Since the given fraction is $\frac{5}{6}$, it becomes $\frac{6}{5}$.
Step 4: Multiply the whole number by the flipped fraction.
Multiply 13 by 6, then divide the answer by 5.
13 × $\frac{6}{5}$ = $\frac{78}{5}$
Step 5: Simply, if necessary.

$\frac{78}{5}$ is equal to 15$\frac{3}{5}$ when simplified or as a mixed fraction.

Example 5

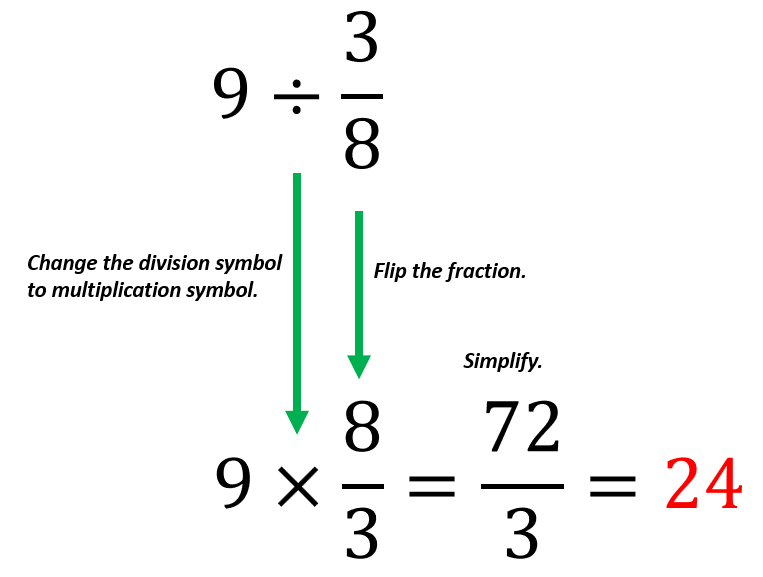
Calculate 9 ÷ $\frac{3}{8}$.

Solution

Let us follow the steps of dividing whole numbers by fractions.

Step 1: We will keep the same whole number, 9.
Step 2: Change the division symbol into the multiplication symbol.
Step 3: Flip the fraction.
Since the given fraction is $\frac{3}{8}$, it becomes $\frac{8}{3}$.
Step 4: Multiply the whole number by the flipped fraction.
Multiply 9 by 8, then divide the answer by 3.
9 × $\frac{8}{3}$ = $\frac{72}{3}$
Step 5: Simply, if necessary.

$\frac{72}{3}$ is equal to 24 when simplified.

Example 6

Solve 25 ÷ $\frac{1}{5}$.

Solution

Let us follow the steps of dividing whole numbers by fractions.

Step 1: We will keep the same whole number, 25.
Step 2: Change the division symbol into the multiplication symbol.
Step 3: Flip the fraction.
Since the given fraction is $\frac{1}{5}$, it becomes $\frac{5}{1}$.
Step 4: Multiply the whole number by the flipped fraction.
Multiply 25 by 5, then divide the answer by 1.
25 × $\frac{5}{1}$ = 125.
Step 5: Simply, if necessary.

125 is the final answer.

Multiplying the Reciprocal of the Fraction

Multiplying the reciprocal of the fraction is a common method for dividing a whole number by a fraction. When we say by the reciprocal of the fraction, it means that we switch the numbers placed in the numerator and the fraction’s denominator. Let us say, for example, we have $\frac{3}{4}$, and its reciprocal is $\frac{4}{3}$. Thus, in dividing a whole number by a fractional number, we must multiply the given whole number by the reciprocal of the given fraction.

Example 1

Find 4 ÷ $\frac{3}{2}$.

Solution

Let us first change the whole number 4 to a fraction by making it $\frac{4}{1}$. Then, multiply it by the reciprocal of the fraction 32, which is 23. Thus, we have,

$\frac{4}{1}$ × $\frac{2}{3}$

Now that we must multiply two fractions, we will first multiply the numerators and then the denominators.

$\frac{4}{1}$ × $\frac{2}{3}$ = $\frac{8}{3}$

Therefore, 4 ÷ $\frac{3}{2}$ = $\frac{8}{3}$ or 2 $\frac{2}{3}$ when simplified or as a mixed fraction.

Example 2

Calculate 7 ÷ $\frac{5}{6}$.

Solution

Let us first change the whole number 7 to a fraction by making it $\frac{7}{1}$. Then, multiply it by the reciprocal of the fraction $\frac{5}{6}$, which is $\frac{6}{5}$. Hence, we have,

$\frac{7}{1}$ × $\frac{6}{5}$

Now that we must multiply two fractions, we will first multiply the numerators and then the denominators.

$\frac{7}{1}$ × $\frac{6}{5}$ = $\frac{42}{5}$

Therefore, 7 ÷ $\frac{6}{5}$ = $\frac{42}{5}$ or 8 $\frac{2}{5}$ when simplified or as a mixed fraction.

Example 3

Solve 11 ÷ $\frac{2}{3}$.

Solution

Let us first change the whole number 11 to a fraction by making it $\frac{11}{1}$. Then, multiply it by the reciprocal of the fraction $\frac{2}{3}$, which is $\frac{3}{2}$. Thus, we have,

$\frac{11}{1}$ × $\frac{3}{2}$

Now that we must multiply two fractions, we will first multiply the numerators and then the denominators.

$\frac{11}{1}$ × $\frac{3}{2}$ = $\frac{33}{2}$

Therefore, 11 ÷ $\frac{2}{3}$ = $\frac{33}{2}$ or 16 $\frac{1}{2}$ when simplified or as a mixed fraction.

Example 4

Calculate 20 ÷ $\frac{4}{5}$.

Solution

Let us first change the whole number 20 to a fraction by making it $\frac{20}{1}$. Then, multiply it by the reciprocal of the fraction $\frac{4}{5}$, which is $\frac{5}{4}$. Thus, we have,

$\frac{20}{1}$ × $\frac{5}{4}$

Now that we must multiply two fractions, we will first multiply the numerators and then the denominators.

$\frac{20}{1}$ × $\frac{5}{4}$ = $\frac{100}{4}$

Therefore, 20 ÷ $\frac{4}{5}$ = $\frac{100}{4}$ or 25 when simplified.

Example 5

Calculate 16 ÷ $\frac{9}{4}$.

Solution

Let us first change the whole number 16 to a fraction by making it $\frac{16}{1}$. Then, multiply it by the reciprocal of the fraction $\frac{9}{4}$, which is $\frac{4}{9}$. Thus, we have,

$\frac{16}{1}$ × $\frac{4}{9}$

Now that we must multiply two fractions, we will first multiply the numerators and then the denominators.

$\frac{16}{1}$ × $\frac{4}{9}$ = $\frac{64}{9}$

Therefore, 16 ÷ $\frac{9}{4}$ = $\frac{64}{9}$ or 7 $\frac{1}{9}$ when simplified or as a mixed fraction.

Example 6

Solve 14 ÷ $\frac{3}{5}$.

Solution

Let us first change the whole number 14 to a fraction by making it $\frac{14}{1}$. Then, multiply it by the reciprocal of the fraction $\frac{3}{5}$, which is $\frac{5}{3}$. Hence, we have,

$\frac{14}{1}$ × $\frac{5}{3}$

Now that we must multiply two fractions, we will first multiply the numerators and then the denominators.

$\frac{14}{1}$ × $\frac{5}{3}$ = $\frac{70}{3}$

Thus, 14 ÷ $\frac{3}{5}$ = $\frac{70}{3}$ or 23 $\frac{1}{3}$ when simplified or as a mixed fraction.

Example Word Problems

Example 1

Suppose a bottle of water holds 6 cups of water. How many ½ cups are required to fill the bottle?

Solution

In this word problem, we must identify the number of ½ cups of water to fill a bottle. Since a full bottle holds 6 cups, we must calculate 6÷½.

Since we are dividing a whole number by a fraction, we must multiply 6 by the reciprocal of ½, which is $\frac{2}{1}$. Here is the math,

6 ÷ $\frac{1}{2}$ = 6 × $\frac{2}{1}$ = 12

Therefore, 12 of ½ cups of water are required to fill the bottle.

Example 2

A food bowl can hold 3 cups of food. A scoop is used to fill the food bowl. Suppose the scoop holds $\frac{1}{3}$ cups of food; how many scoops do you need to fill the food bowl?

Solution

In this word problem, we must identify the number of scoops to fill the food bowl. Since the scoop holds $\frac{1}{3}$ cups of food, we must calculate 3÷$\frac{1}{3}$.

Since we are dividing a whole number by a fraction, we must multiply 3 by the reciprocal of $\frac{1}{3}$, which is $\frac{3}{1}$. Hence, we have,

3 ÷ $\frac{1}{3}$ = 3 × $\frac{3}{1}$ = 9

Therefore, 9 of $\frac{1}{3}$ cups are needed to fill the food bowl.

Example 3

Maria wants to divide 20 full chocolate bars among her students. When she divided the 20 chocolate bars by $\frac{2}{3}$, each student had an equal size of chocolate. How many students does she have?

Solution

In this word problem, we must identify how many students Mary has if she successfully divides 20 by $\frac{2}{3}$.

Since we are dividing a whole number by a fraction, we must multiply 20 by the reciprocal of $\frac{2}{3}$, which is $\frac{2}{2}$. Hence, we have,

20 ÷ $\frac{2}{3}$ = 20 × $\frac{3}{2}$ = $\frac{60}{2}$ =30

Therefore, Mary has 30 students.

Example 4

Mr Davies has 5 pounds of nuts and wants to share them with his friends. Suppose each friend receives $\frac{1}{3}$ pounds; how many friends does he have?

Solution

In this problem, we must calculate the number of friends Mr Davies has. Since he has 5 pounds of nuts, we will divide 5 by $\frac{1}{3}$ or 5 ÷ $\frac{1}{3}$.

To answer the division problem, we must multiply 5 by the reciprocal of $\frac{1}{3}$, which is $\frac{3}{1}$ or just 3. Hence, we have,

5 ÷ $\frac{1}{3}$ = 5 × $\frac{3}{1}$ = $\frac{15}{1}$ = 15

Therefore, Mr Davies has 15 friends.

Summary

When a whole number is divided by a fraction, the number of groups of the fraction that fit inside the whole is determined.

The processes of dividing whole numbers by fractions are as follows:

Multiplying the reciprocal of the fraction is a common method for dividing a whole number by a fraction. When we say by the reciprocal of the fraction, it means that we switch the numbers placed in the numerator and the fraction’s denominator. Let us say, for example, we have $\frac{3}{5}$, and its reciprocal is $\frac{5}{3}$. Thus, in dividing a whole number by a fractional number, we must multiply the given whole number by the reciprocal of the given fraction.

Frequently Asked Questions on Dividing Whole Numbers by Fractions ( FAQs )

What is the meaning of dividing whole numbers by fractions?

When a whole number is divided by a fraction, the number of groups of the fraction that fit inside the whole is determined.

Let us say, for example, we want to calculate 12 ÷ $\frac{3}{4}$. Here, we want to identify how many $\frac{3}{4}$ fit the number 12. It can be solved by multiplying 12 by the reciprocal of $\frac{3}{4}$.

12 ÷ $\frac{3}{4}$ = 12 × $\frac{4}{3}$ = $\frac{48}{3}$ = 16

This means there will be 16 equal groups when 12 is divided by $\frac{3}{4}$.

As for another example, let us calculate 16 ÷ $\frac{2}{5}$. Here, we want to identify how many $\frac{2}{5}$ fit in the whole number 16. This can be solved by multiplying 16 by the reciprocal of $\frac{2}{5}$.

16 ÷ $\frac{2}{5}$ = 16 × $\frac{5}{2}$ = $\frac{80}{2}$ = 40

This means there will be 40 equal groups when 16 is divided by $\frac{2}{5}$.

What is meant by the reciprocal of fractions?

When we say by the reciprocal of the fraction, it means that we switch the numbers placed in the numerator and the fraction’s denominator. Let us say, for example, we have $\frac{2}{5}$, and its reciprocal is $\frac{5}{2}$. As for $\frac{2}{3}$, $\frac{3}{8}$ and $\frac{6}{11}$, their reciprocals are $\frac{3}{2}$, $\frac{8}{3}$ and $\frac{11}{6}$, respectively.

What are the steps for dividing whole numbers by fractions?

The processes of dividing whole numbers by fractions are as follows:

Let us say, for example, we want to calculate 12 ÷ $\frac{5}{7}$.

Let us follow the steps of dividing whole numbers by fractions.

Step 1: We will keep the same whole number, 12.
Step 2: Change the division symbol into the multiplication symbol.
Step 3: Flip the fraction.
Since the given fraction is $\frac{5}{7}$, it becomes $\frac{7}{5}$.
Step 4: Multiply the whole number by the flipped fraction.
Multiply 12 by 7, then divide the answer by 5.
12 × $\frac{7}{5}$ = $\frac{84}{5}$
Step 5: Simply, if necessary.

$\frac{84}{5}$ is equal to 16$\frac{4}{5}$ when simplified or as a mixed fraction.

As for another example, let us calculate 9 ÷ $\frac{3}{5}$.

Let us follow the steps of dividing whole numbers by fractions.

Step 1: We will keep the same whole number, 9.
Step 2: Change the division symbol into the multiplication symbol.
Step 3: Flip the fraction.
Since the given fraction is $\frac{3}{5}$, it becomes $\frac{5}{3}$.
Step 4: Multiply the whole number by the flipped fraction.
Multiply 9 by 5, then divide the answer by 3.
9 × $\frac{5}{3}$ = $\frac{45}{3}$
Step 5: Simply, if necessary.
$\frac{45}{3}$ is equal to 15 when simplified.

What to keep in mind when dividing fractions?

When dividing fractions, the easiest way to follow is to multiply the reciprocal of the divisor by the dividend.

Remember that in a division statement, we have dividend ÷ divisor = quotient. So, let us say we have $\frac{2}{3}$ ÷ $\frac{1}{5}$, $\frac{2}{3}$ is the dividend and $\frac{1}{5}$ is the divisor. To find the quotient, we must multiply $\frac{2}{3}$ by the reciprocal of $\frac{1}{5}$. Hence, to calculate this, we have,

$\frac{2}{3}$ x $\frac{5}{1}$ = $\frac{10}{3}$ = 3$\frac{1}{3}$

Therefore, the quotient is $\frac{10}{3}$ or 3$\frac{1}{3}$ in mixed fractions.

As for another example, let us calculate $\frac{5}{7}$ ÷ $\frac{3}{4}$. To find the quotient, let us multiply $\frac{5}{7}$ by the reciprocal of $\frac{3}{4}$. Thus, we have,

$\frac{5}{7}$ x $\frac{4}{3}$ = $\frac{20}{21}$

Therefore, $\frac{5}{7}$ ÷ $\frac{3}{4}$ = $\frac{20}{21}$

How do we simplify fractions?

Reducing a fraction to its simplest form is the definition of simplifying a fraction. If a fraction’s numerator and denominator are coprime or share only the number one as a common factor, it is said to be in its simplest form. The given fraction is equal to its simplest form.

Let us say, for example, we want to simplify the fraction $\frac{6}{24}$. Let us first list all the factors of the numerator, 6, and the denominator, 24, of the given fraction.

Factors of the numerator, 6: {1, 2, 3, and 6}

Factors of the denominator, 24: { 1, 2, 4, 3, 6, 8, 12, and 24}

The common factors of the numerator, 6, and the denominator, 24, are 2, 3, and 6.

We could divide the numerator and the denominator of the fraction $\frac{6}{24}$ by 2, 3, and 6.

$\frac{6÷2}{24÷2}$ = $\frac{3}{12}$

3/12 is still not in its simplest form since they still have common factors.

$\frac{3÷3}{12÷3}$ = $\frac{1}{4}$.

We could also divide the numerator and the denominator by 3.

$\frac{6÷3}{24÷3}$ = $\frac{2}{8}$

$\frac{2÷2}{8÷2}$ = $\frac{1}{4}$.

If we try dividing both the numerator and the denominator by 6, we have.

$\frac{6÷6}{24÷6}$ = $\frac{1}{4}$.

It is important to note that the easiest way to simplify a given fraction is to divide both its numerator and denominator by their greatest or highest common factor.

Recommended Worksheets

Fractions (Mother’s Day Themed) Math Worksheets
Whole Numbers (Rio Carnival Themed) Math Worksheets
Rounding Whole Numbers (Thousands and Ten Thousands) (International Women’s Day Themed) Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!