Calculating fractions is an essential skill that we must learn as this applies to our daily lives. Just as in other mathematical operations, adding and subtracting fractions involve steps to successfully achieve the result.
Let us say, for example, that your mother bought a whole pizza with eight slices total.
Your brother ate three slices of pizza, while you only ate two.
Which part of the whole pizza did you and your brother eat?
How much of pizza is left?
The solutions to the questions in this word problem can be answered by adding and subtracting fractions.
Before we answer the given problem, let us first recall the following:
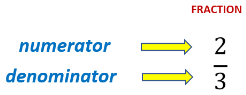
- The value of a fraction indicates the portion of a whole.
- The upper half of the fraction, or numerator, shows the number of parts we have.
- The bottom half of the fraction, or denominator, tells us how many parts make up a whole.
- To simplify a fraction, divide both the numerator and the denominator by their greatest common factor (GCF). For example, if we want to find the GCF of 8 and 12, let us list all their factor.
These are the factors of eight: 1, 2, 4, 8
These are the factors of twelve: 1, 2, 4, 6, 12
The common factors of 8 and 12 are 1, 2, and 4 but the greatest common factor is four. So, to simplify the fraction $\frac{8}{12}$, we have,
$\frac{8 ÷4}{12 ÷ 4}$=$\frac{2}{3}$
It is important to pay attention to the denominators of the given fractions when adding and subtracting fractions to be properly guided on the steps to take in solving them. This article covers steps in adding and subtracting fractions with the same denominators ( like fractions ), different denominators ( unlike fractions ), improper fractions, and mixed fractions.
Adding Fractions with the Same Denominators
Steps in Adding Fractions with the Same Denominators.
Step 1: Take the same denominator from the given fractions.
Step 2: Add the numerators.
Step 3: Simplify the sum.
Let us now answer the word problem given earlier.
Let us say, for example, that your mother bought a whole pizza with eight slices total. Your brother ate three slices of pizza, while you only ate two. Which part of the whole pizza did you and your brother eat?
The fractions below show how much of the whole pizza you and your brother ate.
$\frac{3}{8}$ This is the fraction of the whole pizza that your brother ate.
$\frac{2}{8}$ This is the fraction of the whole pizza that you ate.
Let us follow the steps in adding fractions with the same denominator.
Step 1: Take the same denominator from the given fractions.
$\frac{3}{8}+\frac{2}{8}$ =$\frac{?}{8}$
Step 2: Add the numerators.
$\frac{3}{8}+\frac{2}{8}$ =$\frac{5}{8}$
Step 3: Simplify the sum.
$\frac{5}{8}$ is in its simplest form already since 5 and 8 do not have common factors.
Therefore, $\frac{5}{8}$ is the part of the whole pizza that you and your brother ate.
Examples
Example 1: Find the sum.
- $\frac{1}{7} + \frac{2}{7}$ b. $\frac{1}{9} + \frac{4}{9}$ c. $\frac{5}{12}+\frac{1}{12}$ d. $\frac{2}{5}+\frac{3}{5}$
Solution: To find the sum of the given fractions with the same denominators, we need to add the numerators and copy the same denominator.
Below is a diagram to illustrate the given fractions.



We may simplify $\frac{6}{12}$ by dividing the numerator and denominator by their greatest common factor, which is. To illustrate: $\frac{6 ÷6}{12÷6}$= $\frac{1}{2}$
Therefore,
$\frac{5}{12}+\frac{1}{12}=\frac{6}{12}=\frac{1}{2}$

Since the numerator and the denominator has the same value, then the simplest form of $\frac{5}{5}$ is equal to 1. Thus,

$\frac{2}{5}+\frac{3}{5}=\frac{5}{5}$=1
Example 2: Ryan read $\frac{3}{7}$ of the article yesterday and $\frac{2}{7}$ today.
What fraction of the article has he read?
Solution: $\frac{3}{7} +\frac{2}{7} =\frac{5}{7}$
Hence, Ryan has read $\frac{5}{7}$ of the article.
Subtracting Fractions with the Same Denominator
To subtract fractions with the same denominator, follow these steps.
Step 1: Take the same denominator from the given fractions.
Step 2: Subtract the numerators of the given fractions.
Step 3: Simplify the difference.
Let us continue to answer the follow-up question from the word problem given earlier.
Let us say, for example, that your mother bought a whole pizza with eight slices total. Your brother ate three slices of pizza, while you only ate two. Which part of the whole pizza did you and your brother eat? How much of the pizza is left?
The first question was already answered earlier by adding the parts of the pizza that you and your brother ate, that is, $\frac{3}{8}+\frac{2}{8}=\frac{5}{8}$
Since we want t know the part of the pizza left, we are going to subtract $\frac{5}{8}$ from the whole pizza. Since we have a total of 8 slices and we want to represent the whole pizza in fraction form, we will use $\frac{8}{8}$.
$\frac{8}{8}$ The fraction represents a whole pizza with 8 slices.
$\frac{5}{8}$ The fraction of the pizza that was eaten by you and your brother
Let us now follow the steps in subtracting fractions with the same denominator.
Step 1: Take the same denominator from the given fractions.
$\frac{8}{8}-\frac{5}{8}$ =$\frac{?}{8}$
Step 2: Subtract the numerators of the given fractions.
$\frac{8}{8}-\frac{5}{8} =\frac{3}{8}$
Step 3: Simplify the sum.
$\frac{3}{8}$ is already simplified since 3 and 8 do not have common factors apart from 1.
Thus, $\frac{3}{8}$ is the part of the pizza left.
Examples
Example 1: Find the difference.
a. $\frac{10}{13} – \frac{2}{13}$ b. $\frac{4}{9} – \frac{1}{9}$ c. $\frac{5}{7}-\frac{2}{7}$ d. $\frac{9}{14}-\frac{3}{14}$
Solution: These are examples of subtracting fractions having the same denominators.


The answer $\frac{3}{9}$ is not in simplified form. We must divide both the numerator and the denominator by three ( 3 ) to make the fraction simplified. $\frac{3 ÷ 3}{9 ÷ 3}=\frac{1}{3}$
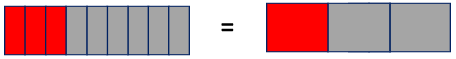
$\frac{4}{9}-\frac{1}{9}=\frac{3}{9}=\frac{1}{3}$
- $\frac{5}{7} – \frac{2}{7}=\frac{3}{7}$
- $\frac{9}{14} – \frac{3}{14}=\frac{6}{14}$
$\frac{6}{14}$ can still be simplified to $\frac{3}{7}$ since the greatest common factor of 6 and 14 is two.
$\frac{6 ÷2}{14 ÷2}=\frac{3}{7}$
Hence, $\frac{9}{14}-\frac{3}{14}=\frac{6}{14}=\frac{3}{7}$
Example 2: Anne saves $\frac{4}{9}$ of her salary. She used $\frac{1}{9}$ of her salary to buy new clothes. What is the fraction of Anne’s remaining salary?
Solution: $\frac{4}{9}- \frac{1}{9} =\frac{3}{9}$
This means that Anne has left $\frac{3}{9}$ of her salary.
Example 3: Nikki used $\frac{2}{9}$ of the day to tidy her room and $\frac{3}{9}$ of the day to finish her homework. What part of the day is she left to do other things?
Solution: Let us first find the time she spent tidying her room and finishing her homework.
$\frac{2}{9}+\frac{3}{9}=\frac{5}{9}$
Therefore, she used a total of $\frac{5}{9}$ of the day.
To answer the part of the day she has left to do other things, we must subtract $\frac{5}{9}$ from $\frac{9}{9}$.
$\frac{9}{9}-\frac{5}{9}=\frac{4}{9}$
Hence, she has left with $\frac{4}{9}$ of the day to do other things.
Adding/ Subtracting Fractions with Different Denominators
Steps in adding fractions with different denominators.
Step 1: Identify the least common denominator ( LCD ) of the given fractions.
Step 2: Multiply the denominator of each of the given fractions by a factor such that the product is the least common denominator in Step 1. Multiply also the same factor to their numerators.
Steps 3-5 follow the steps in adding/ subtracting fractions with the same denominator
Step 3: Take the same denominator from the resulting fractions in Step 2.
Step 4: Add/ Subtract the numerators.
Step 5: Simplify.
Let us consider this diagram and add the fractions $\frac{3}{10}$ and $\frac{2}{5}$.

Following these steps we have,
Step 1: Identify the least common denominator of the given fractions.
$\frac{3}{10} +\frac{2}{5} =\frac{?}{10}$
To find the LCD of fractions, we need to find the least common multiple ( LCM ) of the denominators. Some numbers are multiples of 5 and 10 but we must select the least value among these multiples as shown below.
Multiples of 10: 10 , 20, 30, 40, ….
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45,….
Common Multiples of 5 and 10: 10, 20, 30, 40, 50, 60, ….
Thus, the least common multiple of 5 and 10 is ten (10).
Step 2: Multiply the denominator of each of the given fractions by a factor such that the product is the least common denominator in Step 1. Multiply also the same factor to their numerators.
$\frac{2}{5} x \frac{2}{2} =\frac{4}{10}$
$\frac{3}{10} x \frac{1}{1} =\frac{3}{10}$
Step 3: Take the same denominator from the resulting fractions in Step 2.
$\frac{4}{10} +\frac{3}{10}$=$\frac{?}{10}$
Step 4: Add the numerators.
$\frac{4}{10} +\frac{3}{10}$=$\frac{7}{10}$
Step 5: Simplify.
$\frac{7}{10}$ is in its simplest form.
Examples
Example 1: Find the sum.
$\frac{1}{5}+ \frac{2}{3}$
Solution: This set of given will require us to follow the steps in adding fractions with different denominators. As the process suggests, we need to make the given fractions have the same denominators to make the addition easy.
$\frac{1}{5}+ \frac{2}{3}$
Fifteen ( 15 ) is the least common denominator of 5 and 3.
These are the multiples of 3 : 3 , 6, 9, 12, 15, 18, 21, 24, 27, 30
These are the multiples of 5 : 5 , 10, 15, 20, 25, 30, 25
We will now multiply $\frac{1}{5}$ by $\frac{3}{3}$ and $\frac{2}{3}$ by $\frac{5}{5}$. Thus,
$\frac{1}{5}$ x $\frac{3}{3}$ = $\frac{3}{15}$ ; $\frac{2}{3}$ x $\frac{5}{5}$ = $\frac{10}{15}$
Since we now have the same denominator, we can easily add the fractions and simplify the answer if necessary.
$\frac{3}{15}+ \frac{10}{15}$ = $\frac{13}{15}$
Therefore, $\frac{1}{5}+ \frac{2}{3}$=$\frac{13}{15}$
Example 2: Maricar and Elena are working on their school project. Maricar completed $\frac{1}{3}$ of the project while Elena completed $\frac{1}{2}$ of the project. Which part of the project have they completed in total?
Let us follow the steps in adding fractions with different denominators to answer this question.
Step 1: Identify the least common denominator ( LCD ) of the given fraction.
This is the expression that we must work on
$\frac{1}{2}$+$\frac{1}{3}$
Six ( 6 ) is the LCD of the denominators 2 and 3.
Step 2: Multiply the denominator of each of the given fractions by a factor such that the product is the least common denominator in Step 1. Multiply also the same factor to their numerators.
$\frac{1}{2} x \frac{3}{3} = \frac{3}{6}$ ; $\frac{1}{3} x \frac{2}{2} = \frac{2}{6}$
Step 3: Take the same denominator from the resulting fractions in Step 2.
$\frac{3}{6}+\frac{2}{6}=\frac{?}{6}$
Step 4: Add the numerators.
$\frac{3}{6}+\frac{2}{6}=\frac{5}{6}$
Step 5: Simplify.
The answer is in its simplest form already. Thus, Maricar and Elena have finished working on $\frac{5}{6}$ of the project altogether.
Example 3: Find the difference.
- a. $\frac{7}{12}-\frac{1}{3}$ ; b. $\frac{3}{4}-\frac{1}{6}$
Solution: The process involved here is subtracting fractions with different denominators. Since they are unlike fractions (fractions with different denominators), we must find their least common denominator.
- $\frac{7}{12}-\frac{1}{3}$
Twelve ( 12 ) is the least common multiple of the denominators 3 and 12. Therefore, to make the given fractions have the same denominators, $\frac{7}{12}$ must be multiplied by $\frac{1}{1}$ or simply one while $\frac{1}{3}$ must be multiplied by $\frac{4}{4}$.
$\frac{7}{12} x \frac{1}{1} = \frac{7}{12}$ ; $\frac{1}{3} x \frac{4}{4} = \frac{4}{12}$
We may now proceed with subtracting the fractions with the same denominators.
$\frac{7}{12} – \frac{4}{12} = \frac{3}{12}$
$\frac{3}{12}$ can still be simplified by using three as the divisor to both the numerator and the denominator.
$\frac{3 ÷ 3}{12 ÷ 3}=\frac{1}{4}$
Thus, $\frac{7}{12}-\frac{1}{3}=\frac{1}{4}$.
- $\frac{3}{4} – \frac{1}{6}$
Twelve ( 12 ) is the least common multiple of the denominators 4 and 6.
These are the multiples of 4: 4, 8, 12, 16, 20, 24, …
Multiples of 6: 6, 12, 18, 24, 30,…
Therefore, to make the given fractions have the same denominators we have,
$\frac{3}{4} x \frac{3}{3} = \frac{9}{12}$ ; $\frac{1}{6} x \frac{2}{2} = \frac{2}{12}$
Subtracting the fractions:
$\frac{9}{12} – \frac{2}{12} = \frac{7}{12}$
Thus, $\frac{3}{4}-\frac{1}{6}=\frac{7}{12}$.
Adding/ Subtracting Fractions with Improper Fractions
The steps for adding and subtracting fractions with improper fractions are the same as those previously covered for adding and subtracting fractions. Reducing the improper fraction into a mixed fraction is the only additional step.
Example 1: Add the fractions $\frac{12}{7}+\frac{4}{3}$.
Solution:
Find the LCD of the denominators by identifying the least common multiple of 3 and 7.
Multiples of 7 : 7 , 14, 21, 28, 35, …
Multiples of 3 , 3, 6, 9, 12, 18, 21, 24, 28, 30,…
We will now multiply a number into the fractions such that the product will be twenty-one (21).
$\frac{12}{7} x \frac{3}{3} = \frac{36}{21}$ ; $\frac{4}{3} x \frac{7}{7} = \frac{28}{21}$
Adding these fractions is now easier since they both have the same denominator.
$\frac{36}{21}+\frac{28}{21}=\frac{64}{21}$
Since the sum is an improper fraction, let us convert it to a mixed fraction using division.
64 ÷21=3 with a remainder of 1.
To write this to mixed fraction, $\frac{64}{21}$ is expressed as $3\frac{1}{21}$.
Example 2: Subtract the fractions $\frac{11}{2}-\frac{6}{5}$.
Solution:
Ten is the LCD of the given fractions.
Listing the multiples of 2 : 2, 4, 6, 8, 10, 12, 14, 16, 18, 20,…
Listing the multiples of 10: 10, 20, 30, 40, 50, 60, 70, ….
The next step is to make the two fractions have the same denominators. Thus,
$\frac{11}{2} x \frac{5}{5} = \frac{55}{10}$; $\frac{6}{5} x \frac{2}{2} = \frac{12}{10}$
Let us now add the resulting fractions.
$\frac{55}{10}-\frac{12}{10}=\frac{43}{10}$
Reducing $\frac{43}{10}$ to mixed form will give us $4\frac{3}{10}$. Using division, 43 ÷10=4 remainder three ( 3 ).
Adding/ Subtracting with Mixed Fractions
Method 1: Convert Mixed Fractions to Improper Fractions
Step 1: Perform the conversion of mixed fractions to improper fractions.
Step 2: Scenario 1: If the denominators are the same, take the same denominator.
Scenario 2:If the denominators are different, find the LCD of the denominators.
Multiply the denominator of each of the given fractions by a factor such that the product is the least common denominator. Multiply also the same factor to their numerators.
Step 3: Take the same denominators from Step 2.
Step 4: Add/ Subtract the numerators.
Step 5: Simplify. Express your answer in mixed fractions.
Examples
Example 1: Add the fractions, $2\frac{1}{3}$+$1\frac{2}{5}$.
Step 1: Perform the conversion of the given mixed fractions to improper fractions.
Conversion of a mixed fraction to an improper fraction
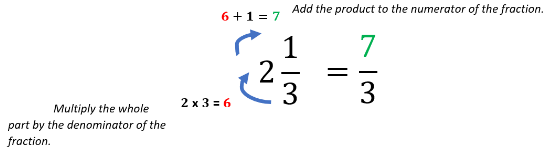
$2\frac{1}{3}=\frac{7}{3}$; $1\frac{2}{5}=\frac{7}{5}$
Step 2: Scenario 2: The fractions have different denominators
Fifteen is the least common multiple of 3 and 5. Thus,
$\frac{7}{3} x \frac{5}{5} = \frac{35}{15}$; $\frac{7}{5} x \frac{3}{3} = \frac{21}{15}$
Step 3: Take the same denominators from Step 2.
$\frac{35}{15} + \frac{21}{15} =\frac{?}{15}$
Step 4: Add/ Subtract the numerators.
$\frac{35}{15} + \frac{21}{15} =\frac{56}{15}$
Step 5: Simplify. Express your answer in mixed fractions.
To express $\frac{56}{15}$ to mixed fractions we have 56 ÷15=3 remainder eleven or $3\frac{11}{15}$
Thus, $2\frac{1}{3}+1\frac{2}{5}=3\frac{11}{15}$
Example 2:
Subtract: $4\frac{2}{3}-2\frac{1}{2}$ .
Solution:
Converting the fractions to mixed form we have,
$4\frac{2}{3}=\frac{14}{3}$; $2\frac{1}{2}=\frac{5}{2}$
We now have $\frac{14}{3}-\frac{5}{2}$. Since they have different denominators, we need to get the least common denominator.
Listing the multiples of 3 : 3 , 6, 9, 12, 15, 18, 21,…
Listing the multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20,…
$\frac{14}{3} x \frac{2}{2} = \frac{28}{6}$; $\frac{5}{2} x \frac{3}{3} =\frac{15}{6}$
Take the same denominator and subtract the numerators.
$\frac{28}{6}-\frac{15}{6} =\frac{13}{6}$
To simplify $\frac{13}{6}$ using division, 13 ÷6=2 remainder 1.
Hence, $\frac{2}{3}-2\frac{1}{2}=2\frac{1}{6}$.
Method 2: Breaking the Mixed Number into wholes and parts.
Step 1: Add/ subtract the whole number part.
Step 2: For the fraction parts,
Scenario 1: If the denominators are the same, take the same denominator.
Scenario 2:If the denominators are different, find the LCD of the denominators.
Multiply the denominator of each of the given fractions by a factor such that the product is the least common denominator. Multiply also the same factor to their numerators.
Step 3: Take the same denominators from Step 2.
Step 4: Add/ Subtract the numerators.
Step 5: Simplify. Express your answer in mixed fractions.
Example
Let us use the same given in Method 1.
Add the fractions, $2\frac{1}{3}+1\frac{2}{5}$.
Step 1: Add/ subtract the whole number part.
2+1=3
Step 2: Scenario 2: The fractions have different denominators
We will be working on $\frac{1}{3}+\frac{2}{5}$.
Fifteen ( 15 ) is the LCD of these fractions.
$\frac{1}{3} x \frac{5}{5} = \frac{5}{15}$; $\frac{2}{5} x \frac{3}{3} =\frac{6}{15}$
Step 3: Take the same denominators from Step 2.
$\frac{5}{15}+ \frac{6}{15} = \frac{?}{15}$
Step 4: Add/ Subtract the numerators.
$\frac{5}{15}+ \frac{6}{15} = \frac{11}{15}$
Step 5: Simplify. Express your answer in mixed fractions.
Whole part : 3 Fraction Part: $\frac{11}{15}$
Therefore, $2\frac{1}{3}+1\frac{2}{5}=3\frac{11}{15}$
Summary
Steps in Adding / Subtracting Fractions with the Same Denominators
Step 1: Take the same denominator from the given fractions.
Step 2: Add/Subtract the numerators of the given fractions.
Step 3: Simplify the sum.
Steps in Adding / Subtracting Fractions with Different Denominators
Step 1: Identify the least common denominator of the fractions given.
Step 2: Multiply the denominator of each of the given fractions by a factor such that the product is the least common denominator in Step 1. Multiply also the same factor to their numerators.
Steps 3-5 follow the steps in adding/subtracting fractions with the same denominator
Step 3: Take the same denominator from the resulting fractions in Step 2.
Step 4: Add / subtract the numerators.
Step 5: Simplify.
Adding/ Subtracting Fractions with Improper Fractions
The steps for adding and subtracting fractions with improper fractions are the same as those previously covered for adding and subtracting fractions. Reducing the improper fraction into a mixed fraction is the only additional step.
Adding/ Subtracting with Mixed Fractions
These are ways to add or subtract mixed fractions.
Method 1: Convert Mixed Fractions to Improper Fractions
Step 1: Perform conversion of the given mixed fractions to improper fractions.
Step 2: Scenario 1: If the denominators are the same, take the same denominator.
Scenario 2:If the denominators are different, find the LCD of the denominators.
Multiply the denominator of each of the given fractions by a factor such that the product is the least common denominator. Multiply also the same factor to their numerators.
Step 3: Take the same denominators from Step 2.
Step 4: Add/ Subtract the numerators.
Step 5: Simplify. Express your answer in mixed fractions.
Method 2: Breaking the Mixed Number into wholes and parts.
Step 1: Add/ subtract the whole number part.
Step 2: For the fraction parts,
Scenario 1: If the denominators are the same, take the same denominator.
Scenario 2:If the denominators are different, find the LCD of the denominators.
Multiply the denominator of each of the given fractions by a factor such that the product is the least common denominator. Multiply also the same factor to their numerators.
Step 3: Take the same denominators from Step 2.
Step 4: Add/ Subtract the numerators.
Step 5: Simplify. Express your answer in mixed fractions.
Recommended Worksheets
Fractions (Mother’s Day Themed) Math Worksheets
Word Problems Involving Fractions (Nutrition Themed) Worksheets
Mixed Numbers (Mother’s Day Themed)









