What are Decimals?
Decimals are a type of number in mathematics that consist of a whole part and a fractional part. The whole part and the fractional part of a decimal are separated by a dot “ . “ .
What are Fractions?
A fraction is a number representing a part of a whole. The whole may be a single or a group of objects. This means that when one whole is divided into equal parts, each part is a fraction. The whole may be a single object or a group of objects. A whole one can be divided into 2 halves or 3 thirds or 4 quarters and so on.
Converting a Decimal to a Fraction
All decimal numbers can be expressed as a fraction. Decimal to fraction conversion is usually a two-step operation.
- First, convert the decimal to fraction using tenths, hundredths, thousandths, etc. depending on the number of decimal places. e.g. 1.75 = 1 75/100.
- Next, simplify the fraction part to the lowest common term. e.g. 75/100 = 3/4.
Fractions and decimals are very similar. In fact, decimal numbers are more correctly known as decimal fractions and fractions with numerators and denominators are, to give them a longer name, common fractions. Help your children to understand that (common) fractions and decimal (fractions) have the same meaning – part of the whole.
Before we move ahead with the conversion of decimals into fractions, it is important to understand the composition of decimals in the place value system.
We know that each place in the place value table has a value ten times the value of the next place on its right. In other words, the value of a place is one-tenth of the value of the next place on its left. We observe that if one digit moves one place left to right its value becomes one-tenth ($\frac{1}{10}$ ) of its previous value and when it moves two places left to right its value comes one-hundredth ( $\frac{1}{100}$ ) of its previous term and so on. Therefore, if we wish to move beyond ones place which is the case of decimals, we will have to extend the place value table by introducing the places of tenths ($\frac{1}{10}$ ), hundredths ($\frac{1}{100}$ ), thousandths ( $\frac{1}{1000}$ ) and so on.
Therefore, the place value table in case of a decimal number will be of the form –
| Thousands ( 1000 ) | Hundreds ( 100 ) | Tens ( 10 ) | Ones ( 1 ) | Tenths ($\frac{1}{10}$) | Hundredths ( $\frac{1}{100}$ ) | Thousandths ( $\frac{1}{1000}$ ) |
For example, the decimal number 257.32 in the place value system will be written as –
| Hundreds | Tens | Ones | Tenths | Hundredths |
| 2 | 5 | 7 | 3 | 2 |
A decimal or a decimal number may contain a whole number part and a decimal part. The following table shows the whole number part and the decimal part of some decimals –
| Number | Whole Number Part | Decimal Part |
| 13.95 | 13 | 95 |
| 9.053 | 9 | 053 |
| 0.148 | 0 | 148 |
| 65.0 | 65 | 0 |
| 17 | 17 | 0 |
| 0.003 | 0 | 003 |
| 0.2 | 0 | 2 |
So, when we say that we are converting a decimal into a fraction, we are actually converting this decimal part into the fractional part.
Let us understand decimals and fractions alike on a number line.
Comparing decimals and fractions on a number line
In order to compare how we write a decimal and its equivalent fraction, let us consider the tenth of a decimal.
Comparing tenth of a decimal to its equivalent fraction
Consider the following figure. It is divided into ten equal parts and one part is shaded. The shaded part represents one-tenth of the whole figure. It is written as $\frac{1}{10}$. $\frac{1}{10}$ is also written as 0.1 which is read as “ point one “ or “ decimal one “.

Thus the fraction $\frac{1}{10}$ is called one-tenth and is written as 0.1.
Also, 1 ones = 10 tenths.
Consider another figure. The below figure is divided into ten equal parts and three parts are shaded. The shaded parts represent three-tenths of the whole figure. It is written as $\frac{3}{10}$. $\frac{3}{10}$ is also written as 0.3 which is read as “ point three “ or “ decimal three “.

Thus the fraction $\frac{3}{10}$ is called three tenth and is written as 0.3.
Also, consider the below figure. The below figure is divided into ten equal parts and six parts are shaded. The shaded parts represent six-tenths of the whole figure. It is written as $\frac{6}{10}$. $\frac{6}{10}$ is also written as 0.6 which is read as “ point six “ or “ decimal six “.

Thus the fraction $\frac{6}{10}$ is called six-tenth and is written as 0.6.
Similarly, $\frac{2}{10}$ , $\frac{4}{10}$ , $\frac{5}{10}$ , $\frac{7}{10}$ , $\frac{8}{10}$ and $\frac{9}{10}$ are called 2-tenths, 4-tenths, 7-tenths, 8-tenths and 9-tenths respectively and are denoted by 0.2 , 0.3 , 0.4 , 0.5 , 0.7 , 0.8 and 0.9 respectively.
Thus we have,
$\frac{1}{10}$ = 0.1 and is called one-tenths or 1 tenths
$\frac{2}{10}$ = 0.2 and is called two-tenths or 2 tenths
$\frac{3}{10}$ = 0.3 and is called three-tenths or 3 tenths
$\frac{4}{10}$ = 0.4 and is called four-tenths or 4 tenths
$\frac{5}{10}$ = 0.5 and is called five-tenths or 5 tenths
$\frac{6}{10}$ = 0.6 and is called six-tenths or 6 tenths
$\frac{7}{10}$ = 0.7 and is called seven-tenths or 7 tenths
$\frac{8}{10}$ = 0.8 and is called eight-tenths or 8 tenths
$\frac{9}{10}$ = 0.9 and is called nine-tenths or 9 tenths
$\frac{10}{10}$ = 1 and is called ten-tenths or 10 tenths
Also, $\frac{11}{10}$ = 11 tenths = 10 tenths + 1 tenths = 1 + $\frac{1}{10}$ = 1 + 0.1 = 1.1
$\frac{12}{10}$ = 12 tenths = 10 tenths + 2 tenths = 1 + $\frac{2}{10}$ = 1 + 0.2 = 1.2
$\frac{13}{10}$ = 13 tenths = 10 tenths + 3 tenths = 1 + $\frac{3}{10}$ = 1 + 0.3 = 1.3
Similarly, we have
$\frac{20}{10}$ = 20 tenths = 10 tenths + 10 tenths = 1 + 1 = 2
$\frac{21}{10}$ = 21 tenths = 20 tenths + 1 tenths = 2 + $\frac{1}{10}$ = 2 + 0.1 = 2.1
$\frac{22}{10}$ = 22 tenths = 20 tenths + 2 tenths = 2 + $\frac{2}{10}$ = 2 + 0.2 = 2.2
Thus a fraction of the form $\frac{Number}{10}$ is written as decimal obtained by putting decimal point by leaving one right-most digit.
For example, $\frac{325}{10}$ = 32.5 while $\frac{5894}{10}$ = 589.4
Thus, above we can relate a decimal and its equivalent fraction.
Comparing hundredth of decimal to its equivalent fraction
If an object is divided into 100 equal parts, then each part is one-hundredth of the whole. This means that –
One thousandth = $\frac{1}{100}$ which in decimal form is equal to 0.01
If we take 7 parts out of 100 equal parts of an object, then 7 parts make $\frac{7}{100}$ of the whole and it is written as 0.07.
Similarly, we have,
$\frac{15}{100}$ = 0.15
$\frac{31}{100}$ = 0.31
$\frac{74}{100}$ = 0.74
$\frac{165}{100}$ = $\frac{100+65}{100}$ = $\frac{100}{100}$ + $\frac{65}{100}$ = 1 + 0.65 = 1.65
$\frac{1145}{1000}$ = $\frac{1100+45}{100}$ = $\frac{1100}{100}$ + $\frac{45}{100}$ = 11 + 0.45 = 11.45 and so on.
So, we can see that the equivalent fraction of the decimal 0.15 will be 15/100.
Comparing thousandth of decimal to its equivalent fraction
If an object is divided into 1000 equal parts, then each part is one-thousandth of the whole. This means that –
One thousandth = $\frac{1}{1000}$ which in decimal form is equal to 0.001
If we take 7 parts out of 1000 equal parts of an object, then 7 parts make $\frac{7}{1000}$ of the whole and it is written as 0.007.
Similarly, we have,
$\frac{15}{1000}$ = 0.015
$\frac{131}{1000}$ = 0.131
$\frac{974}{1000}$ = 0.974
$\frac{1265}{1000}$ = $\frac{1000+265}{1000}$ = $\frac{1000}{1000}$ + $\frac{265}{1000}$ = 1 + 0.265 = 1.265
$\frac{11345}{1000}$ = $\frac{11000+345}{1000}$ = $\frac{11000}{1000}$ + $\frac{345}{1000}$ = 11 + 0.345 = 11.345 and so on.
The examples below show decimals can be shown as common fractions.
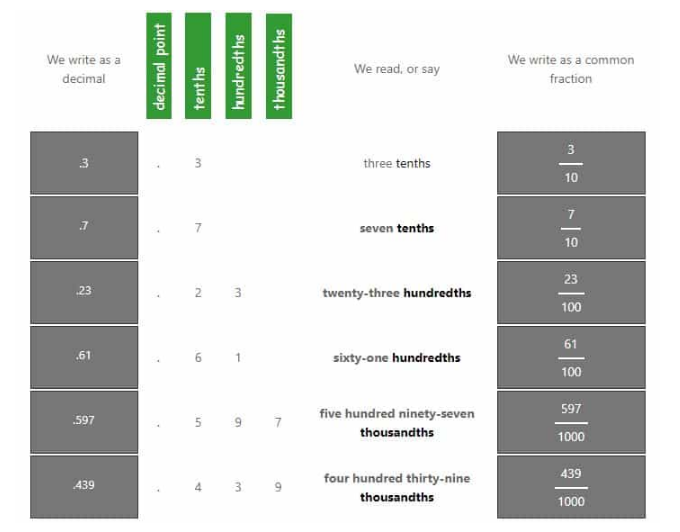
Writing a Fraction in its Simplest Form
To simplify a common fraction we find the greatest common factor for the numerator and the denominator and then use it to divide both. The steps below show an example of how to do this:
| What is the fraction? | 64/100 |
| Find the common factors | 1 , 2 , 4 |
| Find the greatest common factor | 4 |
| Divide 16 (the numerator) by 4 | 64 ÷ 4 = 16 |
| Divide 20 (the denominator) by 4 | 100 ÷ 4 = 25 |
| Write the fraction in simplest form | 16/25 |
Important points regarding simplification of fractions
Given below are some important points that need to be considered while simplification of fractions or reducing them to their lowest form.
- The numerator and denominator of a fraction are called its terms. If we simplify a fraction, then we are reducing it to the lowest terms.
- Reducing a fraction to the lowest terms will not change its value; the reduced fraction will be an equivalent fraction. All we need to do is divide the numerator and the denominator by the same nonzero whole number.
- If the fraction is in mixed form, we first convert it into an improper fraction.
- The result of all four operations on fractions, i.e. addition, subtraction, multiplication and division need to be checked whether the result obtained is in simplified form or not. If not, the fraction should be reduced to its simplest form.
Steps to convert decimals into Fractions
Based on what we have learnt above, we can now define the following steps that will help us convert decimals into their equivalent fractions –
- Obtain the given decimal
- Write the decimal in the form of $\frac{p}{q}$. This can be done by dividing the decimal by 1. For instance, 3.45 can be written as 3.45/1.
- Multiply both top and bottom by 10 for every number after the decimal point. (For example, if there are two numbers after the decimal point, then use 100, if there are three then use 1000, etc.)
- Simplify the given fraction
Let us understand it using an example.
Example
Suppose we wish to convert 3.45 into a fraction
Solution
We have been given the decimal 3.45 and we are required to convert it into a fraction. We shall follow the above steps for this purpose.
First, we will write the given fraction in the form of p/q. we will have,
3.45 = 3.45 / 1
Now, we can see that the given decimal has 2 values after the decimal point. This means we shall multiply and divide this decimal number by 100. We will get
3.45 x $\frac{100}{100}$ = $\frac{345}{100}$
Hence, the equivalent fraction of the decimal 3.45 will be $\frac{345}{100}$. Now we shall simply this fraction so as to reduce it in its simplest form.
We will have
$\frac{345}{100}$ = $\frac{69}{20}$
Hence, the equivalent fraction of the decimal 3.45 will be $\frac{69}{20}$.
Can we convert fractions in the form of decimals in the same manner? Let us find out.
Converting Fractions into decimals
Now, let us observe some examples where we can write fractions as a decimal number as well
Example 1 Write each of the following as a decimal number
- 7 + $\frac{2}{10} + \frac{8}{100} + \frac{6}{1000}$
- $\frac{3}{100} + \frac{7}{1000}$
- $\frac{2}{10} + \frac{3}{100} + \frac{7}{1000}$
Solution We have been given three values in the fractional form and we need to write their equivalent decimal form. Let us do them one by one.
- 7 + $\frac{2}{10} + \frac{8}{100} + \frac{6}{1000}$
We can see that the given fraction has one whole number and three fractional parts. Each one of the given fractional values will be needed to be converted into the corresponding decimal value to get the desired number. So, we have.
7 is a whole number so we need not change into any other form.
We know that $\frac{2}{10}$ = 0.2 and is called two tenths or 2 tenths.
Similarly, $\frac{8}{100}$ = 0.08 and is called eight-hundredths or 8 hundredths
Also, $\frac{6}{1000}$ = 0.006 and is called six thousandths or 6 thousandths
Therefore, the given fraction in the decimal form will be
7 + $\frac{2}{10} + \frac{8}{100} + \frac{6}{1000}$ = 7 + 0.2 + 0.08 + 0.006 = 7.286
- $\frac{3}{100} + \frac{7}{1000}$
We can see that the given fraction has no whole number and two fractional parts. Also, it is important to see that there is no value corresponding to one-tenth of a decimal. Each one of the given fractional values will be needed to be converted into the corresponding decimal value to get the desired number. So, we have.
We will place a 0 for a whole number as there is no whole number value in the given fraction.
Similarly, we will place a 0 for the tenth of a decimal number as there is no value corresponding to one-tenth of a decimal.
Now, $\frac{3}{100}$ = 0.03 and is called three-hundredths or 3 hundredths
Also, $\frac{7}{1000}$ = 0.007 and is called seven thousandths or 7 thousandths
Therefore, the given fraction in the decimal form will be
$\frac{3}{100} + \frac{7}{1000}$ = 0 + 0.0 + 0.03 + 0.007 = 0.037
$\frac{2}{10} + \frac{3}{100} + \frac{7}{1000}$
We can see that the given fraction has no whole number and two fractional parts. Each one of the given fractional values will be needed to be converted into the corresponding decimal value to get the desired number. So, we have.
We will place a 0 for a whole number as there is no whole number value in the given fraction.
We know that $\frac{2}{10}$ = 0.2 and is called two tenths or 2 tenths.
Now, $\frac{3}{100}$ = 0.03 and is called three-hundredths or 3 hundredths
Also, $\frac{7}{1000}$ = 0.007 and is called seven thousandths or 7 thousandths
Therefore, the given fraction in the decimal form will be
$\frac{2}{10} + \frac{3}{100} + \frac{7}{1000}$ = 0.2 + 0.03 + 0.007 = 0.237
Example 2 Write each of the following as decimals
- 20 + 7 + + $\frac{3}{10}$
- 500 + 3 + $\frac{7}{10}$
Solution We have been given an expanded form of two numbers and we are required to find the corresponding decimal number. Let us do them one by one.
- 20 + 7 + + $\frac{3}{10}$
We can see that there are two whole numbers and one fractional number.
Note that the whole values of the given decimal are 20 and 7 and the decimal part is three tenths. Therefore, we will proceed in the same manner as we defined different tenths above.
We will get,
20 + 7 + $\frac{3}{10}$ = 20 + 7 + 0.3 = 27.3
- 500 + 3 + $\frac{7}{10}$
We can see that there are two whole numbers and one fractional number.
Note that the whole values of the given decimal are 500 and 3 and the decimal part is seven tenths. Therefore, we will proceed in the same manner as we defined different tenths above.
We will get,
500 + 3 + $\frac{7}{10}$ = 500 + 3 + 0.7 = 503.7
Key Facts and Summary
- Decimals are a type of numbers in mathematics that consist of a whole parts and a fractional part.
- A fraction is a number representing a part of a whole.
- Fractions and decimals are very similar.
- If an object is divided into 100 equal parts, then each part is one hundredth of the whole.
- The numerator and denominator of a fraction are called its terms. If we simplify a fraction, then we are reducing it to the lowest terms.
- Reducing a fraction to the lowest terms will not change its value; the reduced fraction will be an equivalent fraction. All we need to do is divide the numerator and the denominator by the same nonzero whole number.
- If the fraction is in mixed form, we first convert it into an improper fraction.
- The result of all four operations on fractions, i.e. addition, subtraction, multiplication and division need to be checked whether the result obtained is in simplified form or not. If not, the fraction should be reduced to its simplest form.
Recommended Worksheets
Ordering Decimals (Holi Themed) Math Worksheets
Proper and Improper Fractions (Winter Themed) Math Worksheets
Multiplication of Proper Fractions (Veterans Day Themed) Worksheets









