Introduction
Properties of equality describe the relationship between two quantities that are equal, as well as how an operation maintains the equation’s balance. The equation still holds true when an operation (addition, subtraction, multiplication, and division) is applied to both sides. There are nine properties of equality: addition, subtraction, multiplication, division, reflexive, symmetric, transitive, substitution, and square root.
This article will mainly focus on the subtraction property of equality which states that to maintain equality, if we take a number away from one side of equality, we must also take that same number away from the other side. For greater understanding, this article also includes several examples based on the subtraction property of equality.
What is Subtraction Property?
Definition
According to the algebraic concept known as the “subtraction property of equality,” if a value is subtracted from two equal quantities, the resulting differences are also equal. A mathematical operation known as subtraction is used to balance an equation on both sides of equality. In other words, if two amounts, a and b, are equal and c is subtracted from both a and b, then the difference between a and c is equal to the difference between b and c. The following mathematical formula can be used to express the subtraction property of equality. If a = b, then a – c = b – c.
Let us say, for example, in the illustration below; there are five cubes on each side.
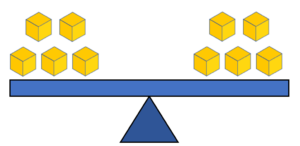
Now, if we take away two cubes from the left side of the scale, as shown below, it creates an imbalance.
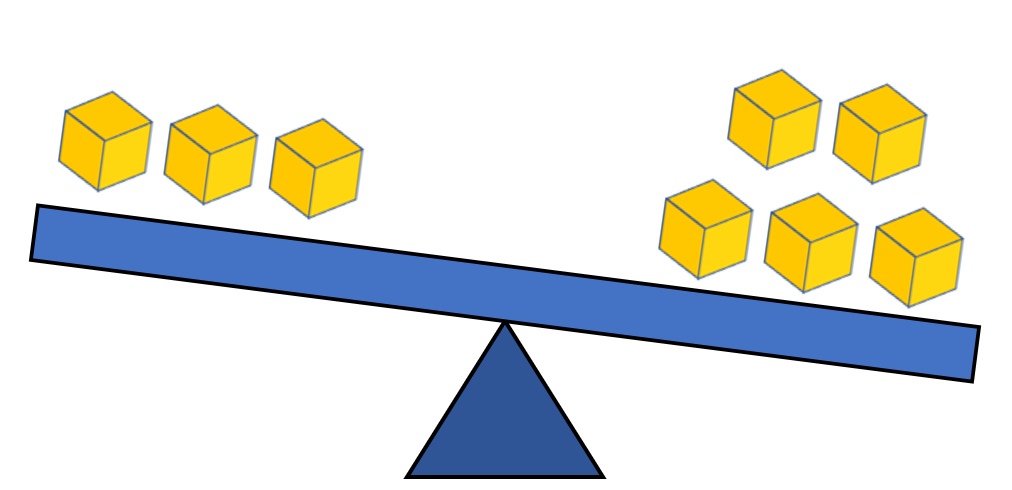
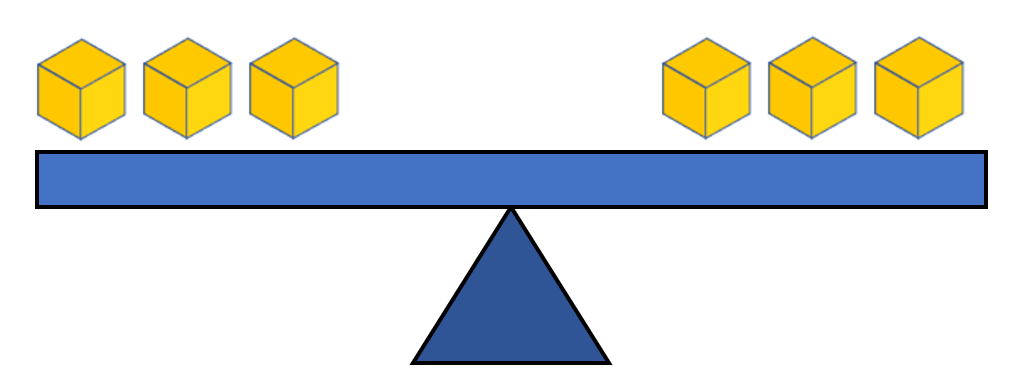
To keep the number of cubes the same on both sides, we must also take away two cubes from the right side of the scale. Hence, after taking two, we now have three cubes left on each side.
Formula: Subtraction Property of Equality
The equality’s subtraction property enables equal quantity to be subtracted from both sides of an equation while maintaining equality.
The following mathematical formula can be used to express the subtraction property of equality.
If a=b,
then a-c=b-c
Let us use the equation 10 + 5 = 15 as an example. When we take 3 out of both sides of the equation, we get,
10 + 5 = 15
10 + 5 – 3 = 15 -3
10 + 2 = 12
This illustrates that equality holds since the same amount was taken away from each side.
Let us take another example using an algebraic equation. Let us have x + 7 = 18. If we want to find the value of x, let us subtract 7 from both sides of the equation. Thus, we have,
x + 7 = 18
x + 7 – 7 = 18 – 7
x = 11
Therefore, the value of x to make the statement true is 11. This also shows how to solve algebraic equations.
Addition Property and Subtraction Property of Equality
Similarities exist between the addition property of equality and the subtraction property of equality.
The equation remains unchanged when the same quantity is added to both sides of an equation, according to the addition property of equality. The addition property, in particular, holds true for both positive and negative values. It is possible to infer the subtraction property of equality from the addition property of equality because subtracting is equivalent to adding a negative.
Let us say we have the equation 20 + 5 = 25. Adding negative 3 to both sides of the equation is the same as subtracting 3 from both sides of the equation
Hence, we have,
20 + 5 = 25
20 + 5 + (-3) = 25 + (-3) Addition Property of Equality
20 + 5 – 3 = 25 – 3 Subtraction Property of Equality
22 = 22
Solving Equations Using the Subtraction Property of Equality
The goal of equation solving is to find the variable value or variables that will make both sides of an equation equal and provide a true statement. The solution of an equation is the value for the variable that makes the equation true.
Let us take the following equations as examples.
( a ) x + 15 = 20
( b ) x + 4 = 15
( c ) 3x – 2x + 6 = 18
( d ) 5x + 5 – 4x + 2 = 16
Solution
( a ) x + 15 = 20
Let us subtract 15 from both sides of the equation using the subtraction property of equality.
x + 15 = 20
x + 15 – 15 = 20 – 15
x = 5
Let us substitute the value in the equation to check if a number is a solution to an equation.
x + 15 = 20
5 + 15 = 20
20 = 20
Since the left-hand side of the equation is equal to the right-hand side, then 5 is a solution to the equation x + 15 = 20.
( b ) x + 4 = 15
By substitution property of equality, we have,
x + 4 = 15
x + 4 – 4 = 15 – 4
x = 11
Let us substitute 11 to the variable x to check if it is a solution to the equation.
x + 4 = 15
11 + 4 = 15
15 = 15
Hence, 15 is a solution to the equation x + 4 = 15.
( c ) 3x – 2x + 6 = 18
Let us first simplify 3x – 2x as x and then use the subtraction property of equality by subtracting 6 to both sides of the equation.
3x – 2x + 6 = 18
x + 6 = 18
x + 6 – 6 = 18 – 6
x = 12
Let us now check if 12 is a solution to the equation.
3x – 2x + 6 = 18
3(12) – 2(12) + 6 = 18
36 – 24 + 6 = 18
18 = 18
Therefore, 12 is a solution to the equation 3x – 2x + 6 = 18.
( d ) 5x + 5 – 4x + 2 = 16
Let us first rearrange the terms and combine like terms.
5x + 5 – 4x + 2 = 16
5x – 4x + 5 + 2 = 16
x + 7 = 16
x + 7 – 7 = 16 – 7
x = 9
Checking if 9 is a solution to the equation, we have,
5x + 5 – 4x + 2 = 16
5(9) + 5 – 4(9) + 2 = 16
45 + 5 – 36 + 2 = 16
16 = 16
It follows that 9 is a solution to the equation 5x + 5 – 4x + 2 = 16 since the left and right sides of the equation are equal.
More Examples
Example 1
Which of the following shows the subtraction property of equality?
- If p = q, then p + r = q + r
- If p = q, then q = p
- If p = q, then p – r = q – r
Solution
Among the properties shown above, the subtraction property of equality is if p = q, then q = p.
The other properties show the addition property of equality and the symmetric property of equality.
- If p = q, then p + r = q + r Addition Property of Equality
- If p = q, then q = p Symmetric Property of Equality
- If p = q, then p – r = q – r Subtraction Property of Equality
Example 2
There are two bags with the same ten candies each. How do the new numbers of candies compare to each other if four candies are taken out of each bag?
Solution
Let: a = number of candies in the first bag ( 10 candies )
b = number of candies in the second bag ( 10 candies )
c = number of candies taken out from each bag ( 4 candies )
Since a = b, let us use the subtraction property of equality to show the four candies taken out from each bag.
a = b
a – c = b – c
10 – 4 = 10 – 4
6 = 6
Therefore, the two bags will still have the same number of candies.
Example 3
At the mall, Gino bought a shirt and a pair of pants. The price of the pants is \$12. Gino paid a total of \$17 on the clothing. How much does the shirt cost?
Solution
Let: x = price of the shirt
\$12 = price of the pair of pants
\$17 = the total cost of the shirt and the pair of pants
Using an equation to represent the situation, we will use x + 12 = 17.
By the subtraction property of equality, we have,
x + 12 = 17
x + 12 – 12 = 17 – 12
x = 5
Let us check if 5 is a solution to the equation by replacing x with it.
x + 12 = 17
5 + 12 = 17
17 = 17
Therefore, the price of the shirt is \$5.
Example 4
Use the subtraction property of equality to find the value of x in each item below.
( a ) x + 12 = 30
( b ) x + 20 = 25
( c ) x + 9 = 17
( d ) x + 4 = 13
( e ) 22 = x + 7
Solution
( a ) x + 12 = 30
x + 12 = 30
x + 12 – 12 = 30 – 12
x = 18
( b ) x + 20 = 25
x + 20 = 25
x + 20 – 20 = 25 – 20
x = 5
( c ) x + 9 = 17
x + 9 = 17
x + 9 – 9 = 17 – 9
x = 8
( d ) x + 4 = 13
x + 4 = 13
x + 4 – 4 = 13 – 4
x = 9
( e ) 22 = x + 7
This is an example of when x is not always on the left side of the equation. The subtraction property of equality still holds in finding the value of x. Hence, we have,
22 = x + 7
22 – 7 = x + 7 – 7
15 = x
15 = x is the same as x = 15.
Hence, the value of x is 15.
Example 5
Using the addition property of equality and subtraction property of equality, how do we find out what x is in the equation x + 8 – 2 = 16?
Solution
To find out what x is using the addition property of equality and subtraction property of equality, we subtract 8 and add 2 on both sides of the equation. Hence, we have,
x + 8 – 2 = 16
x + 8 – 2 – 8 + 2 = 16 – 8 + 2
x = 10
To check if 10 is a solution to the equation, let us replace x with 10 in the equation.
x + 8 – 2 = 16
10 + 8 -2 = 16
16 = 16
Summary
Properties of equality describe the relationship between two quantities that are equal, as well as how an operation maintains the equation’s balance.
According to the algebraic concept known as the “subtraction property of equality,” if a value is subtracted from two equal quantities, the resulting differences are also equal.
The formula for the equality property of subtraction for real numbers a, b, and c is,
If a=b,
then a-c=b-c
The value for the variable that makes an equation true is known as the solution. The goal of solving an equation is to identify the variable value or variables that will make both sides of the equation equal, resulting in a true statement.
Frequently Asked Questions on Subtraction Property of Equality ( FAQs )
What are the properties of equality?
The relationship between two quantities that are equal, as well as how an operation maintains the equation’s balance, are described by properties of equality. The equation holds true when an operation (addition, subtraction, multiplication, and division) is applied to both sides of the equation.
The following are the properties of equality:
| Properties of Equality | |
| Reflexive Property of Equality | p = p |
| Addition Property of Equality | When p = q, then p + r = q + r |
| Subtraction Property of Equality | When p = q, then p – r = q – r |
| Multiplication Property of Equality | When p = q, then p × r = q × r |
| Division Property of Equality | When p = q, then p ÷ r = q ÷ r |
| Transitive Property of Equality | When p = q and q = r, then p = r |
| Substitution Property of Equality | When p = q and p = r, then p = r |
| Symmetric Property of Equality | When p = q, then q = p |
| Square Root Property of Equality | When p2 = q, then p = q |
What is the definition of the subtraction property of equality?
According to the algebraic concept known as the “subtraction property of equality,” if a value is subtracted from two equal quantities, the resulting differences are also equal. A mathematical operation known as subtraction is used to balance an equation on both sides of equality. In other words, if two amounts, a and b, are equal and c is subtracted from both a and b, then the difference between a and c is equal to the difference between b and c. The subtraction attribute of equality can be expressed mathematically as follows: If a = b, then a – c = b – c.
What is the formula of the Subtraction Property of Equality?
The formula for the equality property of subtraction
for real numbers a, b, and c is,
If a = b,
then a – c = b – c
Why can the subtraction property of equality be used to deduce the addition property of equality?
The subtraction property of equality states that
For real numbers a, b, and c
If a = b,
then a – c = b – c
To show that this also means the addition property of equality a + c = b + c, we will subtract -c to both sides of the equation. Hence, we have,
a – (-c) = b – (-c)
a + c = b + c
Thus, for any real numbers a, b, and c, if a = b, then a + c = b + c.
How can equations be solved using the subtraction property of equality?
The value for the variable that makes an equation true is known as the solution. The goal of solving an equation is to identify the variable value or variables that will make both sides of the equation equal, resulting in a true statement.
Recall that according to the algebraic concept known as the “subtraction property of equality,” if a value is subtracted from two equal quantities, the resulting differences are also equal.
The formula for the equality property of subtraction for real numbers a, b, and c is,
If a = b,
then a – c = b – c
Let us use the equation x + 8 = 21 as an example. By the subtraction property of equality to find the value of x, we have,
x + 8 = 21
x + 8 – 8 = 21 – 8
x = 13
Let us check 13 as a solution to the equation by substituting it for the variable x. Thus, we have,
x + 8 = 21
13 + 8 = 21
21 = 21
Therefore, 13 is a solution of the equation x + 8 = 21.
As another example, let us have the equation x + 12 = 36. Using the subtraction property of equality to find the solution to the equation, we have,
x + 12 = 36
x + 12 – 12 = 36 – 12
x = 24
Hence, the value of x that will make the equation true is 24.
What is the Addition Property of Equality?
According to the Addition Property of Equality, adding the same number to both sides of two equal expressions will not affect the expressions’ equality.
The formula for the equality property of subtraction for real numbers a, b, and c is,
If a = b,
then a + c = b + c
What distinguishes the addition property of equality from the subtraction property of equality?
According to the algebraic concept known as the “subtraction property of equality,” if a value is subtracted from two equal quantities, the resulting differences are also equal. A mathematical operation known as subtraction is used to balance an equation on both sides of equality. In other words, if two amounts, a and b, are equal and c is subtracted from both a and b, then the difference between a and c is equal to the difference between b and c.
The formula for the equality property of subtraction for real numbers a, b, and c is,
If a = b,
then a – c = b – c
According to the Addition Property of Equality, adding the same number to both sides of two equal expressions will not affect the expressions’ equality.
The formula for the equality property of subtraction for real numbers a, b, and c is,
If a = b,
then a + c = b + c
Similarities exist between the subtraction property of equality and the addition property of equality.
The equation remains unchanged when the same quantity is added to both sides of an equation, according to the addition property of equality. The addition property, in particular, holds true for both positive and negative values. It is possible to infer the subtraction property of equality from the addition property of equality because subtracting is equivalent to adding a negative.
What is the definition of the Subtraction Property of Inequality?
Equations and inequalities share many similarities. When adding or subtracting from one side of an equation, you must do it on the other side.
According to the inequality’s subtraction property, the inequality remains unchanged if the same amount is subtracted from both sides.
For all real numbers p, q, and r
- If p < q, then p – r < q – r
- If p > q, then p – r > q – r
- If p ≤ q, then p – r ≤ q – r
- If p ≥ q, then p – r ≥ q – r
Recommended Worksheets
Subtraction Table (Rosh Hashanah Theme) Math Worksheets
Subtraction Property (International Dance Day Themed) Math Worksheets
Fact Families for Addition and Subtraction (Christmas Themed) Math Worksheets









