Introduction
Learning number patterns is crucial since it supports the development of a solid mathematical foundation and facilitates dealing with numbers. We will be able to understand the connections between different numbers. Thinking abilities will be improved, including observing sequences and predicting what will happen next.
This article will discuss polygonal numbers that incorporate number patterns, how to describe a sequence of polygonal numbers using dots, and how to determine a given polygonal number depending on its order.
What are polygonal numbers?
Definition
In mathematics, polygonal numbers are nonnegative integers that are represented by regular polygons made of geometrically arranged, evenly spaced points. When the number of equidistant points used to represent a polygon expands, it enlarges in size in a predictable way.
Typically, a geometric figure made up of dots is used to represent polygonal numbers. The number of dots used rises in subsequent polygons, expanding from a central point outward. Triangles, squares, pentagons, and hexagons are the shapes of the first four polygonal numbers.
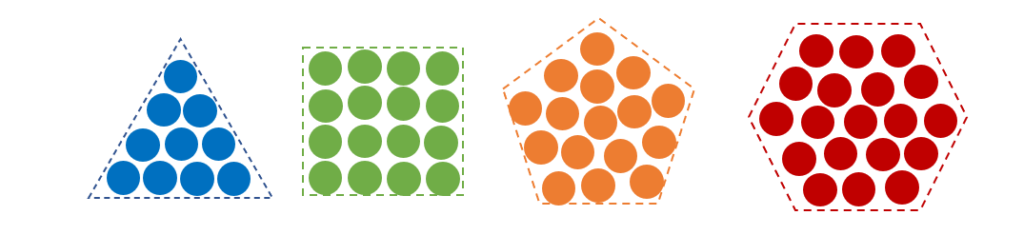
The foundation of polygonal numbers, as demonstrated in the image above, is to consider all polygonal forms and sizes as numerical values. The blue dots represent triangular numbers that fall into the sequence of 1, 3, 6, 10, and so forth. The green dots represent square numbers, which lead to the numbers 1, 4, 9, 16, 25, and so on. The orange dots represent pentagonal numbers in the following order: 1, 5, 12, 22, 35, 51, 70, etc. The sequence of hexagonal numbers, represented by the red dots, is 1, 6, 15, 28, 45, and so forth.
How to find the next polygonal number?
Let us use dots to show the next triangular, square, and pentagonal numbers.
The augmenting array of dots of polygonal numbers has the following stages.
The first polygonal number is always 1.
The polygon’s vertex count is the second number.
The third and subsequent values can be obtained by adding one point to each of two adjacent sides, followed by creating another regular polygon on top of the first.
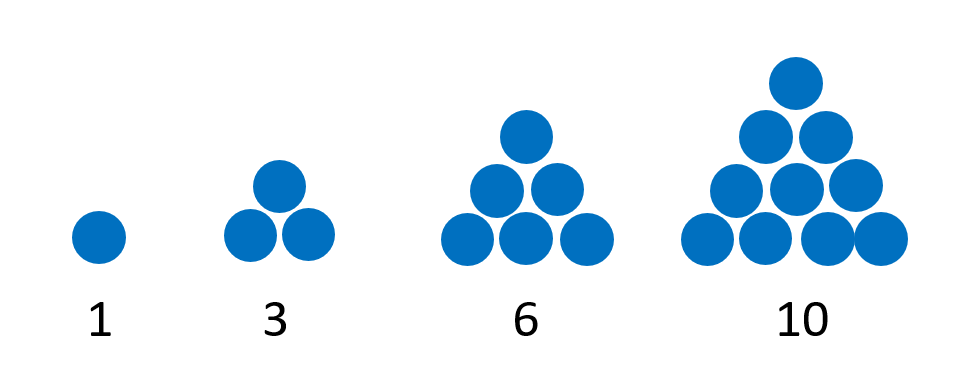
Triangular Numbers
The first triangular number is 1.

The second triangular number is 3 since a triangle has three vertices.
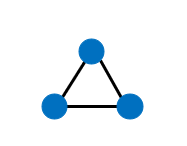
For the third triangular number, we will add one point to each of the two adjacent sides. Equal distances must separate the points. Having three points on each side of a regular triangle, we can now draw another triangle. The third triangular number shows the total number of points.
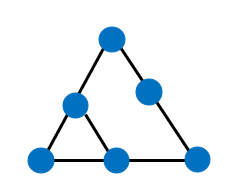
Hence, the third triangular number is 6.
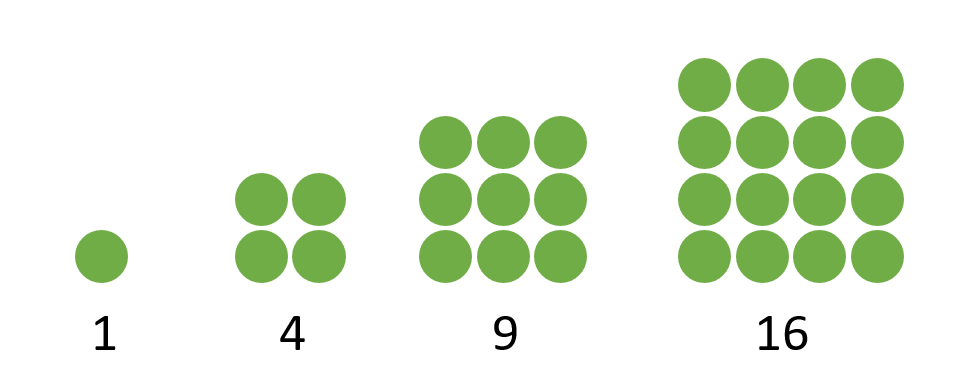
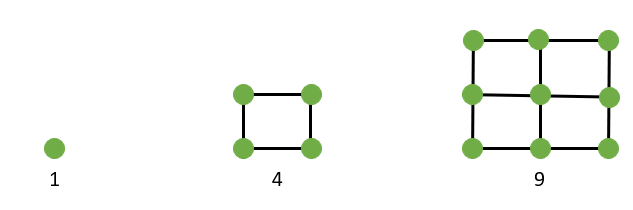
Square Numbers
One is the first square number.

Since a square has four vertices, the second square number is 4.
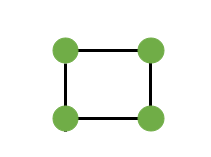
For the third square number, we will add one point to each of the two edges. The points must be separated by equal distances. Now that a regular square has three points on each side, we can design another square. The total number of points shows the third square number.
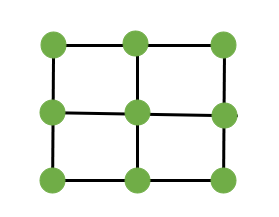
So, 9 is the third square number.
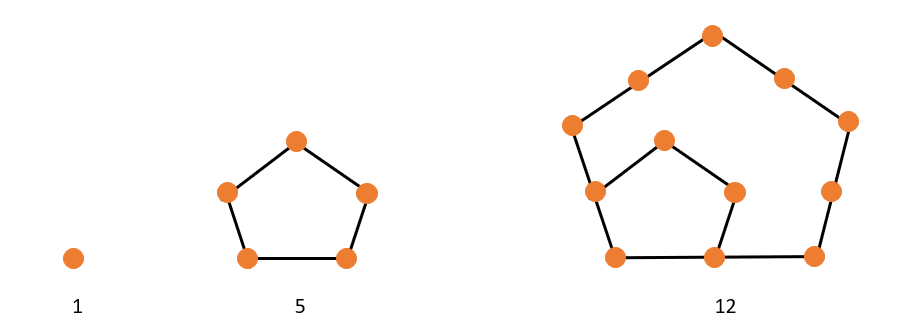
Pentagonal Numbers
One is the first square number.

A pentagon has five vertices; hence 5 is the second square number.

Add one point to each of the two sides to create the third pentagonal number. The points must be separated by identically sized gaps. We may now draw a second pentagon with three points on each side. The total points give the third pentagonal number.
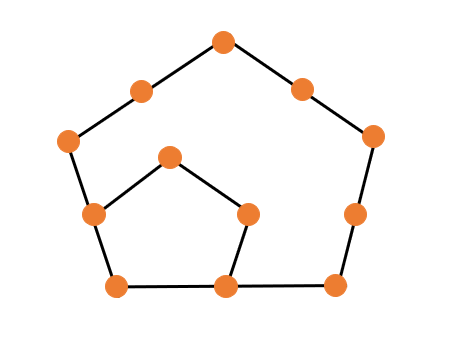
Therefore, 12 is the third pentagonal number.
List of Polygonal Numbers
The following numbers show some of the few triangular, square, pentagonal, and hexagonal numbers.
These are the initial triangular numbers:
| 1, | 3, | 6, | 10, | 15, | 21, | 28, | 36, | 45, | 55, | 66, | 78, | 91, |
| 105, | 120, | 136, | 153, | 171, | 190, | 210, | 231, | 253, | 276, | 300, | 325, | 351, |
| 378, | 406, | 435, | 465, | 496, | 528, | 561, | 595, | 630, | 666, | 703, | 741, | 780, |
| 820, | 861, | 903, | 946, | 990, | 1035, | 1081, | 1128, | 1176, | 1225, | 1275, | 1326, | 1378, |
| 1431, | 1485, | 1540, | 1596, | 1653, | 1711, | 1770, | 1830, | 1891, | 1953, | 2016, | … |
These are the initial square numbers:
| 1, | 4, | 9, | 16, | 25, | 36, | 49, | 64, | 81, | 100, | 121, | 144, | 169, |
| 196, | 225, | 256, | 289, | 324, | 361, | 400, | 441, | 484, | 529, | 576, | 625, | 676, |
| 729, | 784, | 841, | 900, | 961, | 1024, | 1089, | 1156, | 1225, | 1296, | 1369, | 1444, | 1521, |
| 1600, | 1681, | 1764, | 1849, | 1936, | 2025, | 2116, | 2209, | 2304, | 2401, | 2500, | 2601, | … |
These are the initial pentagonal numbers:
| 1, | 5, | 12, | 22, | 35, | 51, | 70, | 92, | 117, | 145, | 176, | 210, | 247, |
| 287, | 330, | 376, | 425, | 477, | 532, | 590, | 651, | 715, | 782, | 852, | 925, | 1001, |
| 1080, | 1162, | 1247, | 1335, | 1426, | 1520, | 1617, | 1717, | 1820, | 1926, | 2035, | 2147, | 2262, |
| 2380, | 2501, | 2625, | … |
These are the initial hexagonal numbers:
| 1, | 6, | 15, | 28, | 45, | 66, | 91, | 120, | 153, | 190, | 231, | 276, | 325, |
| 378, | 435, | 496, | 561, | 630, | 703, | 780, | 861, | 946, | 1035, | 1128, | 1225, | 1326, |
| 1431, | 1540, | 1653, | 1770, | 1891, | 2016, | 2145, | 2278, | 2415, | 2556, | 2701, | 2850, | 3003, |
| 3160, | 3321, | 3486, | … |
The Formula for Finding the nth Polygonal Number
For any natural number n, here are the formulas for triangular, square, pentagonal, and hexagonal numbers.
Triangular Numbers
Tn=$\frac{n ( n+1 )}{2}$
Square Numbers
Sn=n2
Pentagonal Numbers
Pn = $\frac{( 3n^2-n )}{2}$
Hexagonal Numbers
Hn = 2n2 – n
The table below shows the formula’s first four numbers in each sequence.
| Polygon | Formula | n=1 | n=2 | n=3 | n=4 |
| Triangular | Tn=$\frac{n ( n+1 )}{2}$ | T1=$\frac{1 ( 1+1 )}{2}$ T1=1 | T1=$\frac{2 ( 2+1 )}{2}$ T1=3 | T1=$\frac{3 ( 3+1 )}{2}$ T1=6 | T1=$\frac{4 ( 4+1 )}{2}$ T1=10 |
| Square | Sn = n2 | S1 = 12 S1=1 | S2=22 S2=4 | S3=32 S3=9 | S4=42 S4=16 |
| Pentagonal | Pn = $\frac{( 3n^2-n )}{2}$ | P1 = $\frac{( 3(1)^2-1 )}{2}$ P1=1 | P2= $\frac{( 3(2)^2-2 )}{2}$ P2=5 | P3= $\frac{( 3(3)^2-3 )}{2}$ P3=12 | P4= $\frac{( 3(4)^2-4 )}{2}$ P4=22 |
| Hexagonal | Hn = 2n2 – n | H1=2(1)2-1 H1=1 | H2=2(2)2-2 H2=6 | H3=2(3)2-3 H3=15 | H4=2(4)2-4 H4=28 |
The table below shows each sequence’s formulas and the first five numbers.
| Polygon | Formula | n=1 | n=2 | n=3 | n=4 | n=5 |
| Heptagonal | Pn = $\frac{5n^2-3n}{2}$ | 1 | 7 | 18 | 34 | 55 |
| Octagonal | Pn = 3n2 – 2n | 1 | 8 | 21 | 40 | 65 |
| Nonagonal | Pn = $\frac{7n^2-5n}{2}$ | 1 | 9 | 24 | 46 | 75 |
| Decagonal | Pn = (2n)2 – 3n | 1 | 10 | 27 | 52 | 85 |
Sequence on Polygonal Numbers
Triangular Number Sequence
The triangular numbers follow these sequence:
| 1, | 3, | 6, | 10, | 15, | 21, | 28, | 36, | 45, | 55, | 66, | 78, | 91, |
| 105, | 120, | 136, | 153, | 171, | 190, | … |
| a) The first triangular number is 1. b) The second triangular number: 1 + 2 = 3 c) The third triangular number: 1 + 2 + 3 = 6 d) The fourth triangular number is 1 + 2 + 3 + 4 = 10 e) So, any triangular number is equal to the sum of all positive integers up to and including its term number, or, in other words, Tn = 1 + 2 + 3 + 4 + … + n. Thus, T1=1 T2=1+2=3 T3=1+2+3=6 T4=1+2+3+4=10 f) A triangular number can be computed by the formula Tn=$\frac{n ( n+1 )}{2}$. |
Square Number Sequence
The square numbers follow these sequence:
| 1, | 4, | 9, | 16, | 25, | 36, | 49, | 64, | 81, | 100, | 121, | 144, | 169, |
| 196, | 225, | 256, | 289, | 324, | … |
| a) The first square number is 1. b) The second square number is 1 + 3 = 4 c) The third square number is 1 + 3 + 5 = 9 d) The fourth triangular number is 1 + 3 + 5 + 7 = 16 e) Any square number is equal to the sum of n positive odd numbers, hence, Sn = 1 + 3 + 5 + 7 + … + n. f) Notice also that if we square the number position, for example, 12, 22, 33, 42 We will get the square number sequence S1=12=1 S2=22=4 S3=32=9 S4=42=16 So, the next number for the fifth position is 52 =25. A square number can be computed by the formula Sn=n2. |
Pentagonal Number Sequence
The pentagonal numbers follow these sequence:
| 1, | 5, | 12, | 22, | 35, | 51, | 70, | 92, | 117, | 145, | 176, | 210, | 247, |
| 287, | 330, | 376, | 425, | 477, | … |
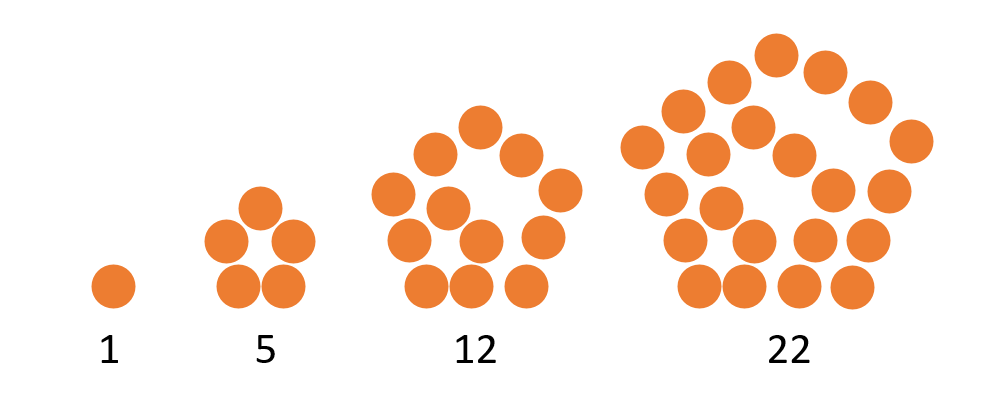
| a) The first pentagonal number is 1. b) The second pentagonal number is 1 + 4 = 5 c) The third pentagonal number is 1 + 4 + 7 = 12 d) The fourth pentagonal number is 1 + 4 + 7 + 12 = 16 e) A pentagonal number can be computed by the formula Pn= $\frac{( 3n^2-n )}{2}$ |
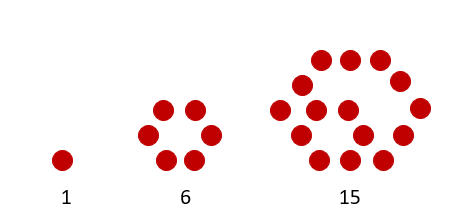
Hexagonal Numbers
The hexagonal numbers follow these sequence:
| 1, | 6, | 15, | 28, | 45, | 66, | 91, | 120, | 153, | 190, | 231, | 276, | 325, |
| 378, | 435, | 496, | 561, | 630, | … |
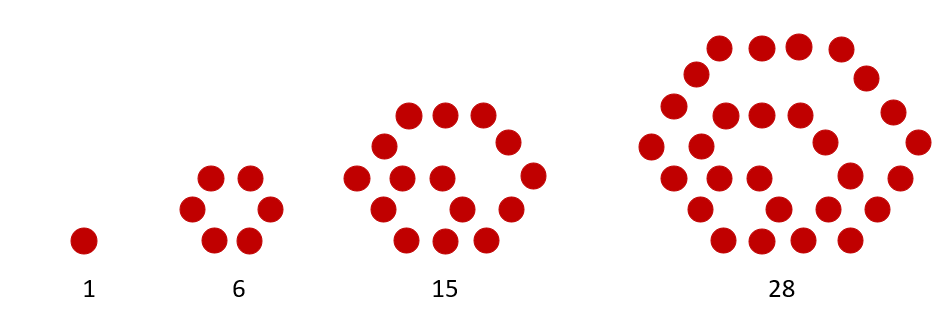
| a) The first hexagonal number is 1. b) The second hexagonal number is 1 + 5 = 6 c) The third hexagonal number is 1 + 5 + 9 = 15 d) The fourth hexagonal number is 1 + 5 + 9 + 13 = 28 e) A hexagonal number can be computed by the formula Hn=2n2-n |
Examples
Example 1
Find each of the following triangular numbers.
( a ) 20th triangular number
( b ) 52nd triangular number
( c ) 44th triangular number
( d ) 100th triangular number
Solution:
To get the missing triangular number, we will use this formula: Tn=$\frac{n ( n+1 )}{2}$
( a ) Since we are solving for the 20th triangular number, we must use n = 20. So, we have,
Tn=$\frac{n ( n+1 )}{2}$
T20=$\frac{20 ( 20+1 )}{2}$
T20=$\frac{20 ( 21 )}{2}$
T20=$\frac{420}{2}$
T20 = 210
Thus, the 20th triangular number is 210.
( b ) We will use n =52 since the missing number is the 52nd triangular number.
Tn=$\frac{n ( n+1 )}{2}$
T52=$\frac{52 ( 52+1 )}{2}$
T52=$\frac{52 ( 53 )}{2}$
T52=$\frac{2756}{2}$
T52 = 1378
Thus, the 52nd triangular number is 1378.
( c ) The number’s position, 44, must be substituted to n to get the 44th triangular number.
Tn=$\frac{n ( n+1 )}{2}$
T44=$\frac{44 ( 44+1 )}{2}$
T44=$\frac{44 ( 45 )}{2}$
T44=$\frac{1980}{2}$
T44=990
Thus, the 44th triangular number is 990.
( d ) Since we are solving for the 100th triangular number, we must use n = 100. So, we have,
Tn=$\frac{n ( n+1 )}{2}$
T100=$\frac{100 ( 100+1 )}{2}$
T100=$\frac{100 ( 101 )}{2}$
T100 = $\frac{10100}{2}$
T100 = 5050
Thus, the 100th triangular number is 5050.
Example 2
Find each of the following square numbers.
( a ) 25th square number
( b ) 42nd square number
( c ) 50th square number
( d ) 65th square number
Solution:
To find the square numbers, we will use the formula Sn=n2
( a ) To find the 25th square number, we must use n = 25. That is,
Sn=n2
S25=252
S25=( 25 )( 25 )
S25 = 625
Thus, the 25th square number is 625.
( b ) We will use n = 42 to find the 42nd square number.
Sn=n2
S42=422
S42= ( 42 )( 42 )
S42=1764
Hence, the 42nd square number is 1764.
( c ) To find the 50th square number, we must use n = 50. That is,
Sn=n2
S50=502
S50=( 50 )( 50 )
S50 = 2500
Thus, the 50th square number is 2500.
( d ) We will use n = 65 to find the 65th square number.
Sn=n2
S65=652
S65= ( 65 )( 65 )
S65=4225
Hence, the 65th square number is 4225.
Example 3
Answer each.
( a ) Find the 8th pentagonal number.
( b ) Which of the following is the 12th pentagonal number? 200, 210, or 220?
( c ) Solve for the 25th pentagonal number.
Solution:
Here is the formula to use in finding the nth pentagonal number: Pn = $\frac{( 3n^2-n )}{2}$
( a ) To find the 8th pentagonal number, we must use n = 8.
Pn = $\frac{( 3n^2-n )}{2}$
P8 = $\frac{( 3(8)^2-8 )}{2}$
P8= $\frac{( 3(64)-8 )}{2}$
P8= $\frac{( 192-8 )}{2}$
P8= $\frac{184}{2}$
P8=92
Therefore, the 8th pentagonal number is 92.
( b ) To find the 12th pentagonal number, we must use n = 12.
Pn = $\frac{( 3n^2-n )}{2}$
P12 = $\frac{( 3(12)^2-12 )}{2}$
P12= $\frac{[ 3 ( 144 )-12 ) ]}{2}$
P12= $\frac{( 432-8 )}{2}$
P12= $\frac{420}{2}$
P12=210
Hence, the 12th pentagonal number is 210.
( c ) The value of n must be 25 to find the 25th pentagonal number.
Pn = $\frac{( 3n^2-n )}{2}$
P25 = $\frac{( 3(25)^2-25 )}{2}$
P25= $\frac{[ 3 ( 625 )-25 ) ]}{2}$
P25= $\frac{( 1875-25 )}{2}$
P25= $\frac{1850}{2}$
P25=925
Thus, the 25th pentagonal number is 925.
Example 4
Find the missing hexagonal numbers.
| 1, | 6, | 15, | 28, | 45, | 66, | 91, | 120, | ______ | 190, | 231, | 276, | 325, |
| 378, | ______ | 496, | 561, | 630, | ______ | 780, | 861, | 946, | 1035, | 1128, | 1225, | ______ |
| 1431, | 1540, | 1653, | 1770, | 1891, | ______ | … |
Solution:
From the given sequence of numbers, we are looking for the 9th,15th, 19th, 26th, and 32nd hexagonal numbers.
Let us use the formula Hn=2n2-n to get the value of the missing hexagonal numbers.
For the 9th hexagonal number, we have,
Hn=2n2-n
H9=2( 9 )2 – 9
H9=2( 81 ) – 9
H9=162-9
H9 = 153
Thus, the 9th hexagonal number is 153.
For the 15th hexagonal number,
Hn=2n2-n
H15=2( 15 )2 – 15
H15=2( 225 )-15
H15 = 450-15
H15 = 435
Thus, the 15th hexagonal number is 435.
To find the 19th hexagonal number, we must use n = 19.
Hn=2n2-n
H19=2( 19 )2 – 19
H19=2( 361 )-19
H19=722-19
H19=703
Therefore, the 19th hexagonal number is 703.
To find the 26th hexagonal number, we must use n = 26.
Hn=2n2-n
H26=2( 26 )2 – 26
H26=2( 676 )-26
H26=1352-26
H26=1326
Therefore, the 26th hexagonal number is 1326.
For the 32nd hexagonal number, we have,
Hn=2n2-n
H32=2( 32 )2 – 32
H32=2( 1024 )-32
H32=2048-32
H32=2016
Thus, the 32nd hexagonal number is 2016.
Here is the list with complete answers for the missing numbers.
| 1, | 6, | 15, | 28, | 45, | 66, | 91, | 120, | 153, | 190, | 231, | 276, | 325, |
| 378, | 435, | 496, | 561, | 630, | 703, | 780, | 861, | 946, | 1035, | 1128, | 1225, | 1326, |
| 1431, | 1540, | 1653, | 1770, | 1891, | 2016, | 2145, | 2278, | 2415, | 2556, | 2701, | 2850, | 3003, |
Example 5
Find the value of the sum of the 12th triangular and the 13th pentagonal numbers.
Solution:
Let us first get the values of the 12th triangular and the 13th pentagonal numbers.
For the 12th triangular number, n = 12.
Tn=$\frac{n ( n+1 )}{2}$
T12=$\frac{12 ( 12+1 )}{2}$
T12=$\frac{12 ( 13 )}{2}$
T12=$\frac{156}{2}$
T12=78
Thus, the 12th triangular number is 78.
For the 13th pentagonal number, the value of n must be 25.
Pn= $\frac{( 3n^2-n )}{2}$
P13= $\frac{[ 3(13)^2-13 ]}{2}$
P13= $\frac{[ 3( 169 )-13 ) ]}{2}$
P13= $\frac{( 507-13 )}{2}$
P13= $\frac{494}{2}$
P13=247
Hence, the 13th pentagonal number is 247.
To answer the question, let us now add 78 and 247 as the 12th triangular and the 13th pentagonal numbers, respectively. So, we have,
78+247=325
Therefore, the sum of the 12th triangular number and the 13th pentagonal number is 325.
Example 6
Find the missing numbers in each polygonal number sequence.
( a ) 1, 3, 6, 10, 15, 21, __, 36, 45, 55, 66, 78, 91, __, 120, 136, 153,
(b ) 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, __, 144, 169, 196, __, 256,
( c ) 1, 5, 12, 22, 35, 51, __, 92, 117, 145, 176, 210, 247, 287, __, 376,
( d ) 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, __, 276, 325, 378, 435, __, 561
Solution:
( a ) The number pattern shows triangular numbers. The 7th and 14th triangular numbers are missing. To get the values of each, let us use this formula: Tn=$\frac{n ( n+1 )}{2}$
For the 7th triangular number, we must use n = 7 while n = 14 for the 14th triangular number.
| Tn=$\frac{n ( n+1 )}{2}$ T7=$\frac{7 ( 7+1 )}{2}$ T7=$\frac{7( 8 )}{2}$ T7=$\frac{56}{2}$ T7=28 | Tn=$\frac{n ( n+1 )}{2}$ T14=$\frac{14 ( 14+1 )}{2}$ T14=$\frac{14( 15 )}{2}$ T14=$\frac{210}{2}$ T14=105. |
Thus, the 7th and 14th triangular numbers are 28 and 105, respectively.
( b ) The set shows the square numbers. We will use the formula: Sn=n2 to find the 11th and 15th square numbers.
| Sn=n2 S11=112 S11=( 11 )( 11 ) S11 = 121 | Sn=n2 S15=152 S15=( 15 )( 15 ) S15 = 225 |
Hence, the 11th square number is 121 while the 15th is 225.
( c ) The sequence’s 7th and 13th pentagonal numbers are missing. Let us use the formula: Pn= $\frac{( 3n^2-n )}{2}$
| Pn= $\frac{( 3n^2-n )}{2}$ P7= $\frac{[ 3(7)^2-7 ]}{2}$ P7= $\frac{[ 3( 49 )-7 ) ]}{2}$ P7= $\frac{( 147-7 )}{2}$ P7=$\frac{140}{2}$ P7=70 | Pn= $\frac{( 3n^2-n )}{2}$ P15= $\frac{[ 3(15)^2-15 ]}{2}$ P15= $\frac{[ 3( 225 )-15 ) ]}{2}$ P15= $\frac{( 675-15 )}{2}$ P15= $\frac{660}{2}$ P15=330 |
Hence, the 7th square number is 70 while the 15th is 330.
( d ) The number pattern shows hexagonal numbers. To get the 11th and 16th hexagonal numbers, let us use this formula: Hn=2n2-n
| Hn=2n2-n H11=2( 11 )2-11 H11=2( 121 )-11 H11=242-11 H11=231 | Hn=2n2-n H16=2( 16 )2-16 H16=2( 256 )-16 H16=512-16 H16=496 |
Therefore, the 11th and 16th hexagonal numbers are 231 and 496.
Summary
Polygonal numbers are nonnegative integers that are represented by regular polygons made of geometrically arranged, evenly spaced points. When the number of equidistant points used to represent a polygon expands, it enlarges in size in a predictable way.
We can find the next polygonal number using dots. The augmenting array of dots of polygonal numbers has the following stages.
The first polygonal number is always 1.
The polygon’s vertex count is the second number.
The third and subsequent values can be obtained by adding one point to each of two adjacent sides, followed by creating another regular polygon on top of the first.
The most common polygonal numbers are triangular numbers, square numbers, pentagonal numbers, and hexagonal numbers.
The first 15 triangular numbers are:
| 1, | 3, | 6, | 10, | 15, | 21, | 28, | 36, | 45, | 55, | 66, | 78, | 91, | 105, | 120 |
The first 15 square numbers are:
| 1, | 4, | 9, | 16, | 25, | 36, | 49, | 64, | 81, | 100, | 121, | 144, | 169, | 196, | 225 |
The first 15 pentagonal numbers are:
| 1, | 5, | 12, | 22, | 35, | 51, | 70, | 92, | 117, | 145, | 176, | 210, | 247, | 287, | 330 |
The first 15 hexagonal numbers are:
| 1, | 6, | 15, | 28, | 45, | 66, | 91, | 120, | 153, | 190, | 231, | 276, | 325, | 387, | 435 |
Formulas in getting the nth polygonal numbers, where n is any natural number,
Triangular Numbers: Tn=$\frac{n ( n+1 )}{2}$
Square Numbers: Sn=n2
Pentagonal Numbers: Pn= $\frac{( 3n^2-n )}{2}$
Hexagonal Numbers: Hn=2n2-n
Frequently Asked Questions on Polygonal Numbers (FAQs)
What is meant by polygonal numbers?
Polygonal numbers are nonnegative integers that are represented by regular polygons made of geometrically arranged, evenly spaced points. When the number of equidistant points used to represent a polygon expands, it enlarges in size in a predictable way.
What is the next polygonal number?
In finding the nth term of polygonal numbers, certain formulas depend on the sequence you are dealing with. The most common set of polygonal numbers is the triangular and square numbers.
Formulas in getting the nth polygonal numbers, where n is any natural number,
Triangular Numbers: Tn=$\frac{n ( n+1 )}{2}$
Square Numbers: Sn=n2
Pentagonal Numbers: Pn= $\frac{( 3n^2-n )}{2}$
Hexagonal Numbers: Hn=2n2-n
How do we use dots to find the next polygonal number?
We can find the next polygonal number using dots. The augmenting array of dots of polygonal numbers has the following stages.
The first polygonal number is always 1.
The polygon’s vertex count is the second number.
The third and subsequent values can be obtained by adding one point to each of two adjacent sides, followed by creating another regular polygon on top of the first.
The first three triangular numbers.

The first three square numbers.
The first three pentagonal numbers.
The first three hexagonal numbers.
Recommended Worksheets
Polygonal Numbers (International Youth Day Themed) Math Worksheets
Cubic Numbers (Constitution Day Themed) Math Worksheets
Co-Prime Numbers (Bastille Day Themed) Math Worksheets









