Numerical patterns are like coded rules that you discover and apply to make number sequences. Number sequences are lists of numbers that follow a pattern. Each numerical pattern, or rule, will create a different number sequence.
Comparing the two sequences and looking for relationships between the numbers can help you understand the rules and the resulting sets of numbers better.
Learning Outcomes
By the end of this lesson, your children will be able to use mathematical rules to correctly generate two different numerical patterns, and then explain how the numbers in the first sequence are related to the numbers in the second sequence
Warm Up
When you began school as a young child, you were immediately introduced to a simple number sequence. You learned to recite all the counting numbers. Usually by the end of Kindergarten, most children can count from 1 to 100. Without even being aware of it, children as young as 3-5 years old are applying a simple sequencing rule to generate the list of numbers to recite. The rule is simply: “Add 1.” By applying this rule over and over again, an unending list of numbers can be created.
1, 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 19…
As you moved on through each grade level, you learned a skill called “skip counting” or “counting by” a certain number. Probably the first skip counting sequence you learned was following the rule: “Add 2.” By applying this rule over and over again, another unending list of numbers can be created.
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, ..
From there you most likely learned to skip count by 5’s, with the rule: “Add 5.”
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, ..
Skip counting began to be called “listing multiples of a number,” or “saying multiplication facts” somewhere around fourth grade. No matter what you were calling it, you were doing algebra: noticing numerical patterns and generating numerical sequences.
Pre-assessment worksheet
Refresh your skip-counting skills with the pre-test to see if you are ready for the lesson on pattern relationships.
Have your children take the Pre-Test that follows to see if they are ready for this lesson. If they get 12 or less correct, review the introduction with them before continuing on to the lesson.
- Generating Patterns & Identifying Relationships – Pre-assessment
Main Lesson: Generating Patterns & Identifying Relationships
Now that you have had a chance to review your skip-counting and number sequences, it’s time to do some comparing.
Starting at zero and using the rule, “Add 3,” we get the sequence:
What do you notice about the numbers?
Look at the two numerical sequences carefully. They both start with zero. Look at the second term from both lists. Then look at the third term from both lists. Continue comparing one term at a time.
Each corresponding term on the second list is twice as big as the term on the first list. Why do you think that is?
The key is in the two rules that were used to generate the sequences. Since the rule “Add 6” is adding twice as much as the rule “Add 3,” The terms on the second list are twice as big as the terms on the first list.
Your children should be observant so they can notice patterns, but make sure that they check all the terms in the sequence before deciding what the pattern is. Similar numbers may appear in different sequences, which could cause the wrong pattern to be identified.
Consider another pair of sequences.
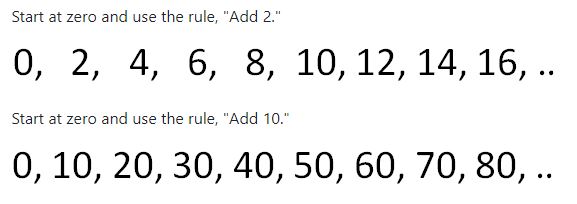
Compare the 2nd term from the 1st list with the 2nd term from the 2nd list. Compare each pair of corresponding terms. Can you tell what the relationship is between the lists? Do you understand why?
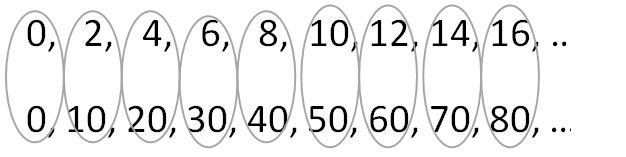
Each corresponding term on the second list is five times as big as the term on the first list. Why do you think that is?
The key is in the two rules that were used to generate the sequences. Since the rule “Add 10” is adding five times as much as the rule “Add 2,” The terms on the second list are five times as big as the terms on the first list.
It’s important to make sure that your children can explain the reasons for patterns that they observe. Being able to explain “why?” forces them to clarify their thinking and deepen their understanding.
Have your children work through the problems in the worksheet below, making sure they consider not only the relationship between the terms in the two numerical sequences, but also the reason for the particular relationship.
Generating and Comparing Sequences – Practice
Recap
- Numerical sequences are made by applying a rule.
- Missing numbers in a sequence can be found by looking at the numbers that are in the sequence, and determining the rule.
- Numerical sequences can be compared.
- The relationship between two rules can be seen in the relationship between the corresponding terms in the two numerical sequences that they create.
Test Questions
Review the above recap points with your children and then print out the Post Test that follows.
- Numerical Patterns & Relationships – Post-assessment
At least 3 out of 4 correct will show that your children are ready to go on to the next lesson: Ordered Pairs And Coordinate Plane Graphing.
