Different Types of Addition and Subtraction Situations
In our day to day situations, we come across different problems that relate to addition and subtraction in mathematics. For instance, if you buy a few items from a grocery store, you will need to check the bill raised by the store by adding the costs of the items purchased. Similarly, there might be a situation when you need to find the difference between the original and the discounted price of an item. Such situations make it necessary for students to have a strong grasp of the understanding of the concepts of addition and subtraction. However, this cannot be achieved without enough practice.
Important Terms and Keywords in addition and subtraction
Below are some important terms and keywords that are associated with addition and subtraction –
| how many | how much | leftover | still to go |
| additional | together | combined | add |
| both | sum | increase | difference |
| total | change | more | decrease |
| fewer | spent | reduce | remaining |
| less |
Let us discuss some such situations which can be useful in the understanding of these terms.
Situations where we use the term “Add To”
Below are some situational problems where we make use of the term “ Add To ”–
- There are three fishes in a pond. Four more fish are added to the pond. How many fishes are there in the pond now?
We have been given –
Number of fishes in the pond = 3
Number of more fishes added to the pond = 4
For obtaining the total number of fishes in the pond now, we will have to add the number of fishes added to the pond to the number of fishes that were present in the pond earlier. Therefore,
3 + 4 = 7 this is the total number of fishes in the pond now
- There are 2 tigers in a forest. Five more tigers are brought from the nearby forest. How many tigers are there in the forest now?
We have been given –
Number of tigers in the forest = 2
Number of more tigers brought in from nearby forest = 5
For obtaining the total number of tigers in the forest now, we will have to add the number of tigers brought in from the nearby forest to the number of tigers that were present in the forest earlier. Therefore,
2 + 5 = 7 this is the total number of tigers in the forest now
Situations where we use the term “Put Together”
We could have used the term put together as well in the above questions. For instance, the question in the example above could be rephrased as –
- There are three fishes in a pond. Four more fish are added to the pond. How many fishes are there in the pond put together?
Similarly, the second question could also be rephrased as –
- There are 2 tigers in a forest. Five more tigers are brought from the nearby forest. How many tigers are there in the forest put together?
Situations where we use the term “Take From”
Below are some situational problems where we make use of the term “Take From”–
- On his birthday, James placed 12 burning candles on the cake. He blew nine of them. How many of the candles were burning on the cake now?
We have been given –
Number of candles burning on the cake = 12
Number of candles blown by James = 9
For obtaining the total number of candles burning on the cake now, we will have to take the number of candles left burning on the cake from the number of candles that were burning on the cake earlier. Therefore,
12 – 9 = 3 this is the total number of candles left burning on the cake
- There were 16 mangoes on a tree. Samuel plucked 9 of them. How many mangoes were left on the tree?
We have been given –
Number of mangoes on a tree = 15
Number of mangoes plucked by Samuel = 9
For obtaining the total number of mangoes left on the tree now, we will have to take the number of mangoes plucked by Samuel from the number of mangoes on a tree earlier. Therefore,
15 – 9 = 6 this is the total number of mangoes left on the tree now
Situations where we use the term “Compare”
Below are some situational problems where we make use of the term “Compare”–
- Jack scored 25 marks in a test while Peter scored 38 marks in the same test. How many more marks did Peter score as compared to Jack?
We have been given –
Marks scored by Jack in a test= 25
Marks scored by Peter in the same test = 38
For obtaining additional marks scored by Peter, we shall compare his marks with that of Jack. We will have,
25 + ________ = 38
= 13
Hence, Peter scored 13 more marks as compared to Jack.
- Michael has 13 playing cards while Alice has 22 playing cards. How many more playing cards does Alice have as compared to Michael?
We have been given –
Number of cards that Michael has = 13
Number of cards that Alice has = 22
For obtaining additional cards that Alice has as compared to Michael, we shall compare the number of cards that Alice has with that of Michael. We will have,
13 + ________ = 22
= 9
Hence, Alice has 9 more cards as compared to Michael.
Does more always mean to add?
It is usually assumed that the term “ more “ means to add. However, that is not the case. At times, when we ask questions such as “ How much more is A than B “, this means that we need to find the difference between A and B or in other words subtract them.
Common Errors
There are some common mistakes when it comes to solving word problems on addition and subtraction. Some of these are –
- Calculation errors – You need to be extremely careful when adding or subtracting numbers as often it is seen that students make mistakes when working in a careless manner.
- Proper explanation – When it comes to working on word problems, it is important to mention proper statements so as to explain the steps undertaken correctly. These include mentioning what is given, what needs to be calculated and the formula intended to be used for this purpose.
- Understanding of the Problem – One of the most common errors is when a student fails to identify whether the problem needs a solution through addition or subtraction.
Addition and Subtraction Word problems Involving Money
We know that money is available in different forms at different places. For buying things we use coins and notes which are issued by the respective governments of the country we live in. These are called currency. Let us discuss some money-related situations where we make use of addition or subtraction
Example
Suppose, Gracia purchased two items, one at the cost of £ 2.05 while another at the cost of £ 4.20. What is the total cost she needs to pay altogether?
Solution
We have been that given that Gracia purchased two items, one at the cost of £ 2.05 while another at the cost of £ 4.20. We need to find out how much Gracia needs to pay altogether. There are two ways of doing it. Either we add the money directly or first convert the given amounts in pence. We know that
£ 1 = 100 p
Therefore, we have,
£ 2.05 = 2.05 x 100 = 205 p
£ 4.20 = 4.20 x 100 = 420 p
Now we have two values 205 p and 420 p. we can add these values, in the same manner, we add two whole numbers. We will get,
205 p + 420 p = 625 p
Now we have obtained our result in pence. To convert it back into pounds, we will have to divide the result by 100. We will now have,
625 p = £ $\frac{625}{100}$ = £ 6.25
Hence, we can say that the sum of £ 2.05 and £ 4.20 = £ 6.25
A direct way of solving this problem would have been to add the two amounts directly. We would then have,
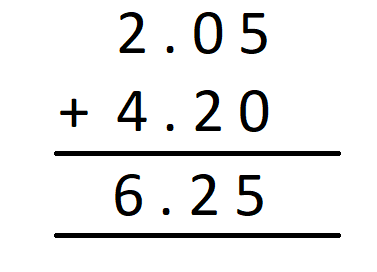
It is important to note here that irrespective of the method we use, we shall get the same result.
Let us consider another example.
Example
Maria purchased a syrup for £ 36.00, a cookies box for £ 29.50 and a hair oil bottle for £ 32.50. If she gave the shopkeeper £ 100, how much money did the shopkeeper return as balance?
Solution
We have been given that Maria purchased a syrup for £ 36.00, a cookies box for £ 29.50 and a hair oil bottle for £ 32.50. She gave the shopkeeper £ 100. We are required to find the money returned by the shopkeeper as a balance. In order to do so, first, let us summarise the items purchased by Maria.
Cost of syrup purchased by Maria = £ 36.00
Cost of cookies box purchased by Maria = £ 29.50
Cost of hair oil bottle purchased by Maria = £ 32.50
Total shopping by Maria = £ 36.00 + £ 29.50 + £ 32.50 = £ 98
Now, Maria gave £ 100 to the shopkeeper. Therefore
Change returned by the shopkeeper = £ 100 – £ 98 = £ 2.00 Change returned by the shopkeeper = £ 100 – £ 98 = £ 2.00
Hence, Maria got £ 2.00 from the shopkeeper as a change.
Addition and Subtraction Word problems Involving Decimals
We perform addition and subtraction of decimals in many situations in our day-to-day lives. For example, you may need to add up your grocery bill before paying at the counter. Have you ever noticed that most of the prices are in decimals? Let us discuss through an example where we use addition or subtraction of decimals in our daily life.
Example
Sophie had £ 305.80 in her bank account. She deposited £ 250.25 more and then withdrew £ 317.50 from her account. What is the balance now in her account?
Solution
Let us first define what is given and what needs to be calculated. We have been given that Sophie had £ 305.80 in her bank account. She deposited £ 250.25 more and then withdrew £ 317.50 from her account. We are required to find the balance in her account now. Therefore,
Initial amount in Sophie’s account = £ 305.80 …………………. ( 1 )
The amount deposited by Sophie = £ 250.25 …………………. ( 2 )
Both the decimal numbers are like terms; hence we can go ahead with the calculations.
Total amount in Sophie’s account = ( 1 ) + ( 2 )
= £ 305.80 + £ 250.25
= £ 556.05 …………………………… ( 3 )
Now, from this total amount, Sophie had withdrawn £ 317.50
Therefore, money left in her account = ( 3 ) – £ 317.50
Again, both the decimal numbers are like terms; hence we can go ahead with the calculations.
= £ 556.05 – £ 317.50
= £ 238.55
Hence, money left in Sophie’s account = £ 238.55
Let us take another example.
Example
Sam, Peter and Henry bought 8.5 litres, 7.25 litres and 9.4 litres of milk respectively from a milk booth. How much milk did they buy in all? If there were 30 litres of milk in both, find the quantity of milk left.
Solution
Let us first define what is given and what needs to be calculated. We have been given that Sam, Peter and Henry bought 8.5 litres, 7.25 litres and 9.4 litres milk respectively from a milk booth. We need to find out –
a) How much milk did they buy in all?
b) If there were 30 litres of milk in both, find the quantity of milk left.
Let us find the answers to the above problems one by one.
Amount of milk bought by Sam = 8.5 litres
Amount of milk bought by Peter = 7.25 litres
Amount of milk bought by Henry = 9.4 litres
The total amount of milk bought by them = 8.5 litres + 7.25 litres + 9.4 litres
Note here that the given decimals are not like terms. Hence, we will first need them to be converted into like terms. Therefore, we now have,
Amount of milk bought by Sam = 8.5 litres = 8.50 litres
Amount of milk bought by Peter = 7.25 litres = 7.25 litres
Amount of milk bought by Henry = 9.4 litres = 9.40 litres
Now that the terms are like terms, we can go ahead with the calculations.
Total milk bought by Sam, Peter and Henry = 8.50 litres + 7.25 litres + 9.40 litres = 25.15 litres
Hence, the total milk bought by Sam, Peter and Henry =25.15 litres
Now, let us solve the second part of the question. We have been given that there were 30 litres of milk in the booth. How much milk is left after Sam, Peter and Henry bought the milk?
Therefore,
Total milk in booth = 30 litres
Milk bought by Sam, Peter and Henry = 25.15 litres
Again, we can see here that the given decimals are not like terms. Hence, we will first need them to be converted into like terms. Therefore, we now have,
Total milk in booth = 30 litres = 30.00 litres
Milk bought by Sam, Peter and Henry = 25.15 litres
Now that the terms are like terms, we can go ahead with the calculations.
Milk left in the booth = 30.00 litres – 25.15 litres
= 4.85 litres
Hence, after Sam, Peter and Henry, 4.85 litres of milk was left in the booth.
Addition and Subtraction Word problems Involving Fractions
It is not just money or decimals, we find everyday situations where we need to solve word problems involving addition and subtraction. We are required to do so in the case of fractions as well. Let us look at some situations where we encounter addition and subtraction word problems involving fractions –
Example
A recipe needs 3/7 teaspoon black pepper and 1/4 teaspoon red pepper. How much more black pepper does the recipe need?
Solution
We have been given that a recipe needs 3/7 teaspoon black pepper and 1/4 teaspoon red pepper. We need to find out how much more black pepper is required in the recipe as compared to red pepper.
First of all, we will summarise the fractions given to us. We have,
Fraction of black pepper needed in the recipe = $\frac{3}{7}$
Fraction of red pepper needed in the recipe = $\frac{1}{4}$
In order to find out how much more black pepper is required in the recipe as compared to red pepper, we will need to find the difference between the black pepper and the red pepper used.
Therefore, we need to find out the value of $\frac{3}{7} – \frac{1}{4}$
The denominators of the above fractions are different; therefore, we will find their L.C.M first.
L.C.M of 7 and 4 = 28
Now, we will convert the given fractions into equivalent fractions with denominator 28.
$\frac{3}{7} = \frac{3 x 4}{7 x 4} = \frac{12}{28}$
$\frac{1}{4} = \frac{1 x 7}{4 x 7} = \frac{7}{28}$
Now, that the denominator of both the fractions is the same we will find the difference in their numerators. We have,
$\frac{3}{7} – \frac{1}{4} = \frac{12}{28} – \frac{7}{28} = \frac{12- 7}{28} = \frac{5}{28}$
Hence, the amount of more black pepper required in the recipe as compared to red pepper = $\frac{5}{28}$
Recommended Worksheets
Fact Families for Addition and Subtraction (Christmas Themed) Math Worksheets
Problem Solving – Addition and Subtraction (World Teachers’ Day Themed) Math Worksheets
Solving Word Problems involving Addition and Subtraction of numbers within 120 1st Grade Math Worksheets









