What is a percent?
Percent or percentage is a value that denotes the hundredth part of any quantity, which is represented by a percent symbol, %. A percent is also referred to as the ratio or fraction wherein the whole is always equal to 100. It is a dimensionless number – meaning it does not have a unit of measurement.
In essence, percent means for every hundred. Percent originated from the Latin word per centum, which means “by a hundred.”
Like fractions, percent cannot be over 100 as there is no way you have more parts than a whole. Sometimes, percentages that are more than 100% don’t make any sense. Consider using 100% of your effort. That means you’ve given everything you have to offer, and 100% is all the effort you have, no more, no less.
Let’s look at the examples of how percent looks like.
| EXAMPLES | |
| 10% | Percent is usually written using whole numbers and percent symbol. |
| 0.01% | Percent can also be written using decimals. |
| 5.5% | A combination of whole numbers and decimals can also be an example of a percentage. |
| $\frac{1}{4}$% | Percent with fractions is also an example of percentage. |
| $9\frac{1}{5}$% | Percent with mixed numbers is also considered as an example of percentage. |
How to convert percent to decimals?
A percent is a ratio with a base of 100. Conversions between percent and decimal are the most obvious and easy process to do. The simplest way to convert percent to decimals is by simply moving two decimal places from right to left.
Percent with whole numbers and decimals
When changing percent with whole numbers to decimal, simply follow the steps below:
- Remove the percent symbol.
- Divide the number by 100 or simply move two decimal places from right to left.
Example #1
Convert 15% to decimals
Solution
| Step-by-step process | Explanation |
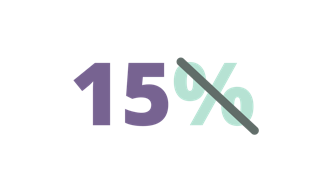 | Remove the percent symbol. Hence, we will have 15. |
| 15 ÷ 100 = 0.15 | Divide 15 by 100. You can also move two decimal places from right to left. |
| Therefore, 15% is equivalent to 0.15 in decimals. |
Example #2
What is 2.3% when converted to decimals?
Solution
| Step-by-step process | Explanation |
 | Remove the percent symbol. Thus, we will start the process by using 2.3 |
| 2.3 ÷ 100 = 0.023 | Divide 2.3 by 100. You can also do the shortcut method wherein you simply move two decimal places from right to left. |
| Therefore, 2.3% is the same as 0.023 in decimals. |
Example #3
Find the equivalent of 0.9% in decimals.
Solution
| Step-by-step process | Explanation |
 | Remove the percent symbol. Hence, we will start by using 0.9 |
| 0.9 ÷ 100 = 0.009 | Divide 0.9 by 100 or simply move two decimal places from right to left. |
| Therefore, 0.9% is equivalent to 0.009 in decimals. |
Example #4
Determine the equivalent of 0.88% in decimals.
Solution
| Step-by-step process | Explanation |
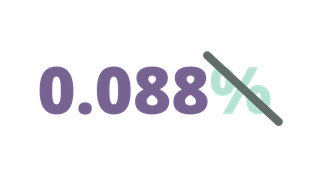 | Remove the percent symbol. Thus, we will begin the process by using 0.88. |
| 0.088 ÷ 100 = 0.00088 | Divide 0.088 by 100 or move two decimal places from right to left. |
| Therefore, 0.088% is equivalent to 0.00088 in decimals. |
Take note not to be caught out by the temptation to always place the decimal point to the left of the digits in the decimal.
Percent with fractions
To convert percent with fractions to decimals, follow the steps below:
- Remove the percent symbol.
- If the given fraction is a mixed number, convert to an improper fraction. Otherwise, do step 3.
- Multiply $\frac{1}{100}$ to the result.
- Divide the numerator by the denominator.
Example #1
What is the equivalent of $\frac{4}{5}$% in decimals?
Solution
| Step-by-step process | Explanation |
 | Remove the percent symbol. Thus, we will start by using $\frac{4}{5}$. |
| $\frac{4}{5} × \frac{1}{100} = \frac{4}{500}$ | Multiply $\frac{4}{5}$ by $\frac{1}{100}$. Hence, the result will be $\frac{4}{500}$. |
| 4 ÷500 = 0.008 | Divide the numerator by the denominator. Hence, 4 ÷ 500 = 0.008 |
| Therefore, the equivalent of $\frac{4}{5}$% to decimals is 0.008. |
Example #2
Find the equivalent of $10\frac{6}{7}$% in decimals?
Solution
| Step-by-step process | Explanation |
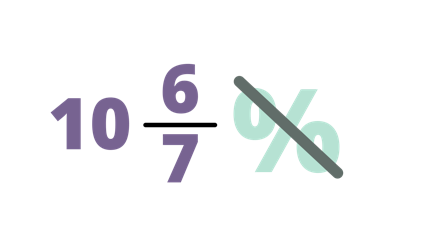 | Remove the percent symbol. Thus, we will start by using $10\frac{6}{7}$. |
| $10\frac{6}{7} → \frac{76}{7}$ | Change the mixed number to improper fraction. |
| $\frac{76}{7} × \frac{1}{100} = \frac{76}{700}$ | Multiply $\frac{76}{700}$ by $\frac{1}{100}$. Hence, the result will be $\frac{76}{700}$. |
| $\frac{76 ÷ 4}{700 ÷ 4}= \frac{19}{175}$ | Simplify the fraction by finding the GCF of 76 and 700. Since their GCF is 4, we need to divide it to 76 and 700. Thus, 76 ÷ 4 = 19700 ÷ 4 = 175 |
| 19 ÷175 = 0.1086 | Divide the numerator by the denominator. |
| Therefore, the equivalent of $10\frac{6}{7}$% to decimals is 0.1086. |
How to convert decimals to percent?
When converting decimals to percent, we multiply the number by 100 or move two decimal places from left to right. However, when converting decimals that mostly have two decimal places (e.g. 0.32), it can be easy to think of just removing the decimal place.
To convert decimals to percent, we simply do the following steps:
- Multiply the decimals by 100 or move two decimal places from left to right.
- Add the percent symbol.
Example #1
What is 0.7 in percent?
Solution
| Step-by-step process | Explanation |
| 0.7 x 100 = 70 | Multiply 0.7 by 100. You can also do the shortcut method where we simply move two decimal places from left to right. |
| 70% | Add the percent symbol |
| Therefore, 0.7 is the same as 70% in percentage. |
Example #2
Convert 0.45 to percent.
Solution
| Step-by-step process | Explanation |
| 0.45 x 100 = 45 | Multiply 0.45 by 100 or simply move two decimal places from left to right. |
| 45% | Add the percent symbol. |
| Therefore, 0.45 is the same as 45% when converted to percent. |
Example #3
Find the equivalent of 0.064 in percent.
Solution
| Step-by-step process | Explanation |
| 0.064 x 100 = 6.4 | Multiply 0.064 by 100 or simply move two decimal places from left to right. |
| 6.4% | Add the percent symbol. |
| Therefore, 0.064 is equivalent to 6.4%. |
Example #4
What is the equivalent of 0.0013 to percent?
Solution
| Step-by-step process | Explanation |
| 0.0013 x 100 = 0.13 | Multiply 0.0013 by 100 or simply move two decimal places from left to right. |
| 0.13% | Add the percent symbol. |
| Therefore, 0.0013 is equivalent to 0.13%. |
How to convert percent to fractions?
Percent can be written as fractions as they both represent a part of a whole.
Percent with whole numbers
To convert percent with whole numbers to fractions, follow the steps below:
- Remove the percent symbol.
- Write the number on the numerator.
- Write 100 on the denominator.
- Simplify, if possible.
Example #1
Convert 10% to fraction.
Solution
| Step-by-step process | Explanation |
 | Remove the percent symbol. Hence, we will now have 10. |
| $\frac{10}{}$ | Write 10 on the numerator of the fraction. |
| $\frac{10}{100}$ | Put 100 on the denominator. Thus, we will have $\frac{10}{100}$. |
| $\frac{10 ÷10}{100 ÷ 10}= \frac{1}{10}$ | Simplify the fraction. Since 10 and 100 are both divisible by 10, we will divide both numbers by 10. Hence, 10 ÷ 10 = 1100 ÷10=10 |
| Therefore, when converted to a fraction, 10% will be $\frac{1}{10}$. |
Example #2
What is 39% when converted to fraction?
Solution
| Step-by-step process | Explanation |
 | Remove the percent symbol. Thus, we have 39. |
| $\frac{39}{}$ | Put 39 on the numerator of the fraction. |
| $\frac{39}{100}$ | Write 100 on the denominator. Hence, we will have $\frac{39}{100}$. Since 39 and 100 do not have a GCF, then $\frac{39}{100}$ is the simplified form. |
| Therefore, 39% is the same as $\frac{39}{100}$ when written in fraction. |
Example #3
What is the equivalent of 58% in fraction?
Solution
| Step-by-step process | Explanation |
| Remove the percent symbol. Hence, we will now have 58. | |
| $\frac{10}{}$ | Write 58 on the numerator of the fraction. |
| $\frac{58}{100}$ | Write 100 on the denominator. Thus, we will have $\frac{58}{100}$. |
| $\frac{58 ÷ 2}{100 ÷ 2}= \frac{29}{50}$ | Simplify the fraction by finding the GCF of 58 and 100. Since their GCF is 2, we will divide 58 and 100 by 2. 58 ÷ 2 = 29100 ÷ 2 = 50 |
| Therefore, 58% is equivalent to $\frac{29}{50}$. |
Percent with decimals
To convert percent with decimals to fractions, follow the steps below:
- Remove the percent symbol.
- Write the number on the numerator.
- Write 100 on the denominator.
- Multiply the numerator by a number to make it a whole number.
- Multiply the same number on the denominator.
- Simplify, if possible.
Example #1
Convert 9.8% to fraction.
Solution
| Step-by-step process | Explanation |
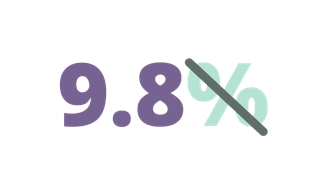 | Remove the percent symbol. Hence, we will now have 9.8. |
| $\frac{9.8}{}$ | Write 9.8 on the numerator of the fraction. |
| $\frac{9.8}{100}$ | Write 100 on the denominator. |
| $\frac{9.8 × 10 = 98}{100}$ | Convert the numerator to a whole number by multiplying 9.8 by 10. Hence,9.8 x 10 = 98 |
| $\frac{98}{100 × 10 = 1000}$ | Since we multiplied the numerator by 10, we also need to multiply the denominator by 10. Thus, 100 x 10 = 1000 |
| $\frac{98 ÷ 2}{1000 ÷ 2}= \frac{49}{500}$ | Simplify the fraction by finding the GCF of 98 and 100. Since their GCF is 2, we will it to the numerator and denominator. Hence, 98 ÷ 2 = 491000 ÷ 2 = 500 |
| Therefore, 9.8% is equivalent to $\frac{49}{500}$. |
Example #2
What is the equivalent of 0.05% to fraction?
Solution
| Step-by-step process | Explanation |
 | Remove the percent symbol. Hence, we will now have 9.8. |
| $\frac{0.05}{100}$ | Write 0.05 on the numerator and 100 on the denominator. |
| $\frac{0.05 × 100 = 5}{100}$ | To convert the 0.05 to a whole number, we need to multiply 100 to it. Hence,0.05 x 100 = 5 |
| $\frac{5}{100 × 100 = 10000}$ | Since we multiplied 100 to the numerator, we need to the same thing on the denominator. Hence, 100 x 10 = 1000. |
| $\frac{5 ÷ 5}{10000 ÷ 5}= \frac{1}{2000}$ | Reduce the fraction to its simplest form by finding the GCF of 5 and 10000. Since both numbers are divisible by 5, hence,5 ÷ 5 = 110000 ÷ 5 = 500 |
| Therefore, 0.05% is the same as $\frac{1}{1200}$ when converted to fraction. |
Percent with fractions
To convert percent with fractions and mixed numbers to fractions, follow the steps below:
- Remove the percent symbol.
- If the given fraction is a mixed number, convert to improper fraction. Otherwise, do step 3.
- Multiply the fraction by $\frac{1}{100}$.
- Simplify, if possible.
Example #1
What is the equivalent of $\frac{3}{4}$% to fraction?
Solution
| Step-by-step process | Explanation |
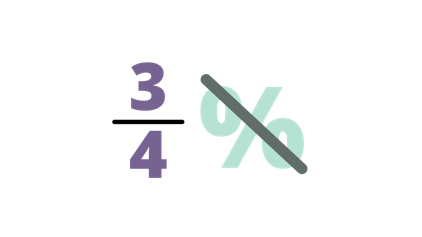 | Remove the percent symbol. Hence, we will have $\frac{3}{4}$. |
| $\frac{3}{4} × \frac{1}{100} = \frac{3}{400}$ | Multiply $\frac{3}{4}$ by $\frac{1}{100}$. Hence, we will have the result of $\frac{3}{400}$. |
| Therefore, $\frac{3}{4}$% is equivalent to $\frac{3}{400}$. |
Example #2
What is $\frac{8}{9}$% when converted to fraction?
Solution
| Step-by-step process | Explanation |
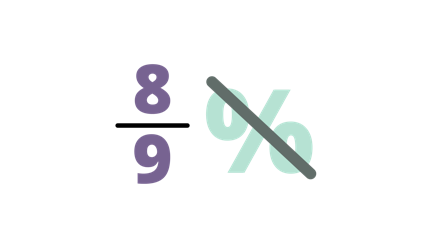 | Remove the percent symbol. Thus, we will start by using $\frac{8}{9}$. |
| $\frac{8}{9} × \frac{1}{100} = \frac{8}{900}$ | Multiply $\frac{8}{9}$ by $\frac{1}{100}$. Hence, the result will be $\frac{8}{900}$. |
| $\frac{8 ÷ 4}{900 ÷ 4}= \frac{2}{225}$ | Simplify the fraction by finding the GCF of 8 and 900. The GCF of the two number is 4. Thus, 8 ÷ 4 = 2900 ÷ 4 = 225 |
| Therefore, $\frac{8}{9}$% is equivalent to $\frac{2}{225}$. |
Example #3
Convert $6\frac{2}{5}$% to fractions.
Solution
| Step-by-step process | Explanation |
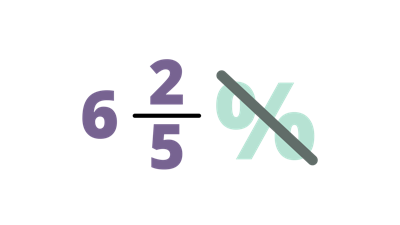 | Drop the percent symbol. Hence, we start with $6\frac{2}{5}$. |
| $6\frac{2}{5} → \frac{32}{5}$ | Change $6\frac{2}{5}$ to improper fraction. |
| $\frac{32}{5} × \frac{1}{100} = \frac{32}{500}$ | Multiply $\frac{1}{100}$ to $\frac{32}{500}$. |
| $\frac{32 ÷ 4}{500 ÷ 4}= \frac{8}{125}$ | Simplify the fraction by finding the GCF of 32 and 500. Since their GCF is 4, divide it to 32 and 500 numbers. Thus, 32 ÷ 4 = 8500 ÷ 4 = 125 |
| Therefore, $6\frac{2}{5}$% is equivalent to $\frac{8}{125}$ when converted to fractions. |
How to convert fractions to percent?
There are also many situations in language where, for example, stating “approximately one-third” would be more appropriate than stating “approximately 33.3%”. Very often, when expressing a fraction as a percent, you will need to round to a certain number of decimal places. The easiest way to convert from a fraction to a percent is to divide the numerator by the denominator and then multiply by 100.
To convert fractions to percent, follow the steps below:
- Divide the numerator by the denominator.
- Multiply the result by 100.
- Add the percent sign.
Example #1
What is the equivalent of $\frac{21}{100}$ to percent?
Solution
| Step-by-step process | Explanation |
| 21 ÷ 100 = 0.21 | Divide the numerator by the denominator. |
| 0.21 x 100 = 21 | Multiply 0.21 by 100 or simply move two decimal places from left to right. |
| 21% | Add the percent symbol. |
| Therefore, $\frac{21}{100}$ is equivalent to 21%. |
Example #2
Convert $\frac{1}{5}$ to percent.
Solution
| Step-by-step process | Explanation |
| 1 ÷5 = 0.2 | Divide the numerator by the denominator. In the given fraction, 1 is the numerator and 5 is the denominator. |
| 0.2 x 100 = 20 | Multiply 0.2 by 100. You can also use the shortcut method by simply moving two decimal places from left to right. |
| 20% | Add the percent symbol. |
| Therefore, $\frac{1}{5}$ is equivalent to 20%. |
Example #3
What is the equivalent of $\frac{5}{8}$ to percent?
Solution
| Step-by-step process | Explanation |
| 5 ÷8 = 0.625 | Divide the numerator by the denominator. |
| 0.625 x 100 = 62.5 | Multiply 0.625 by 100 or simply move two decimal places from left to right. |
| 62.5% | Add the percent symbol. |
| Therefore, $\frac{5}{8}$ is the same as 62.5%. |
Example #4
Find the equivalent of $\frac{2}{3}$ to percent.
Solution
| Step-by-step process | Explanation |
| 2 ÷3 = 0.6667 | Divide the numerator by the denominator. Get at least 4 decimal places of the result. |
| 0.6667 x 100 = 66.67 | Multiply 0.6667 by 100 or simply move two decimal places from left to right. |
| 66.67% | Add the percent symbol. |
| Therefore, $\frac{2}{3}$ is equivalent to 66.67% when converted. |
Example #5
Convert $\frac{4}{7}$ to percent.
Solution
| Step-by-step process | Explanation |
| 4 ÷ 7 = 0.5714 | Divide the numerator by the denominator. Get at least 4 decimal places of the result. |
| 0.5714 x 100 = 57.14 | Multiply 0.5714 by 100 or simply move two decimal places from left to right. |
| 57.14% | Add the percent symbol. |
| Therefore, $\frac{4}{7}$ is equivalent to 57.14% when converted. |
Common percentage and its equivalent in fractions and decimals
Memorizing or at least being able to quickly recall the equivalent percent, decimals, and fractions listed below will be of great assistance to students as they tackle problems that require changing between the different types. Quick recall of these will also help in everyday-type-situations such as comparing price discounts. e.g. what is the best deal, one-third off, or 25% off?
| PERCENT | DECIMALS | FRACTIONS |
| 1% | 0.01 | $\frac{1}{100}$ |
| 5% | 0.05 | $\frac{1}{20}$ |
| 10% | 0.1 | $\frac{1}{10}$ |
| 20% | 0.2 | $\frac{1}{5}$ |
| 25% | 0.25 | $\frac{1}{4}$ |
| 50% | 0.5 | $\frac{1}{2}$ |
| 75% | 0.75 | $\frac{3}{4}$ |
| 80% | 0.8 | $\frac{4}{5}$ |
| 90% | 0.9 | $\frac{9}{10}$ |
| 100% | 1 | 1 |
Recommended Worksheets
Percents and Discounts (Thanksgiving Themed) Math Worksheets
Applying Percentage, Base, and Rate 6th Grade Math Worksheets
Percentages Worksheets









