Definition
Ten-Frames are two-by-five rectangular frames into which objects like counters can be placed to show numbers less than or equal to ten. Ten frames are often used as learning tools for numbers up to 10. In other words, a ten frame is a rectangle with ten equal spaces. There are five spaces on the top and five spaces on the bottom. Below is a representation of what a ten frame looks like –
How to prepare Ten Frames
The following steps should be followed to make ten frames –
- First, make a frame of ten equal spaces. These spaces should be placed in the form of a rectangle having five spaces on the top and five spaces at the bottom.
- Always fill the top row first, starting from the left. The ten frames are also read in the same manner.
- When the top row is full, then process with placed filling counters at the bottom. Again it is important to note here that the bottom row is also to be filled from the left.
In this way, a standard manner can be used to make ten frames
Uses of Ten Frames
Ten frames are useful in the following manner –
- They are often used as learning tools for numbers up to 10.
- Ten frames help with developing number sense.
- Ten frames are useful in understanding the relationships of numbers, especially for the numbers from 1 to 10.
- Ten frames help the children visualise the numbers which make it easier for them to understand about working with numbers.
- Ten frames are useful in making the children understand the composing and decomposing of numbers.
Operations where ten frames are used
Ten frames find their use in understanding the addition and subtraction of numbers up to 10. So, the following are the areas where we can extensively use ten frames as a learning tool –
Let us learn more about them.
Counting numbers on ten frames
Ten frames can be used effectively to help a child in learning of counting of numbers from 1 to 10.
Let us first list down the numbers from 1 to 10. We have,
Number Number Name
1 One
2 Two
3 Three
4 Four
5 Five
6 Six
7 Seven
8 Eight
9 Nine
10 Ten
Now, let us understand the representation of these numbers using ten frames.
1 ( One )

2 ( Two )
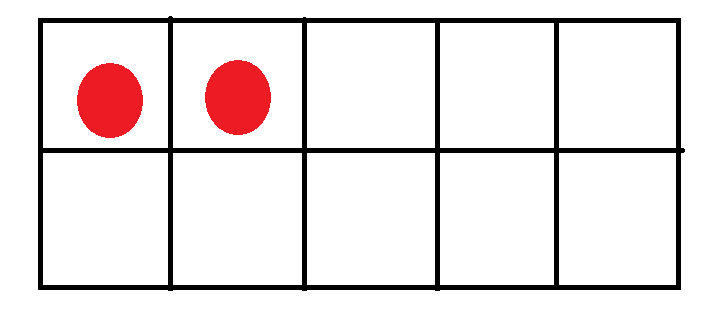
3 ( Three )
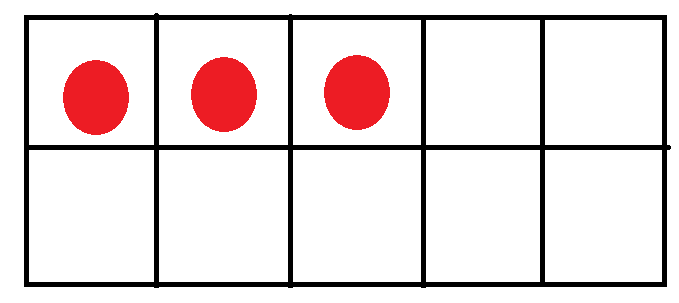
4 ( Four )
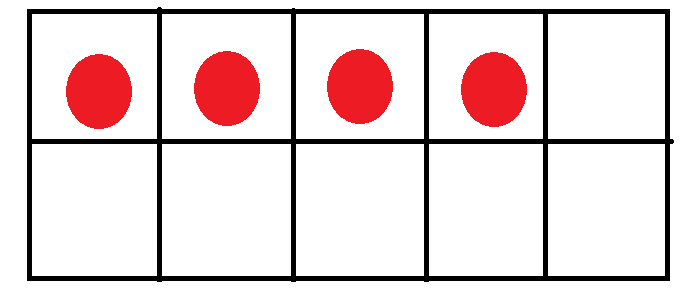
5 ( Five )
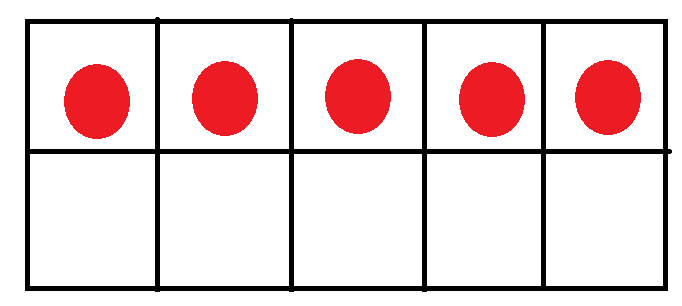
6 ( Six )
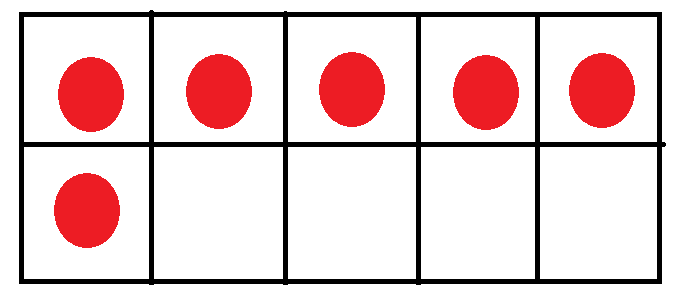
7 ( Seven )
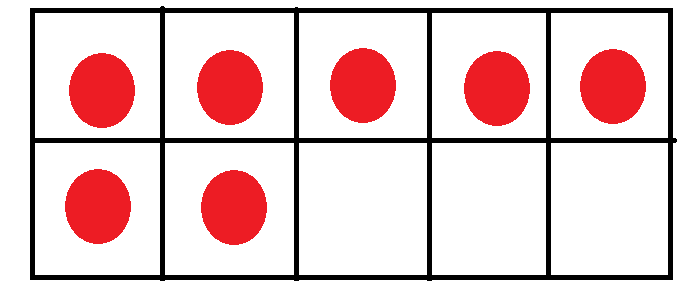
8 ( Eight )
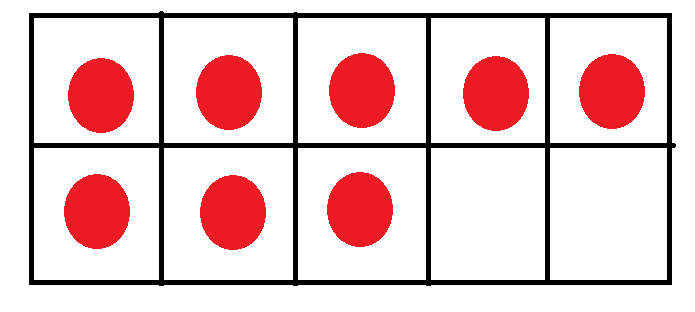
9 ( Nine )
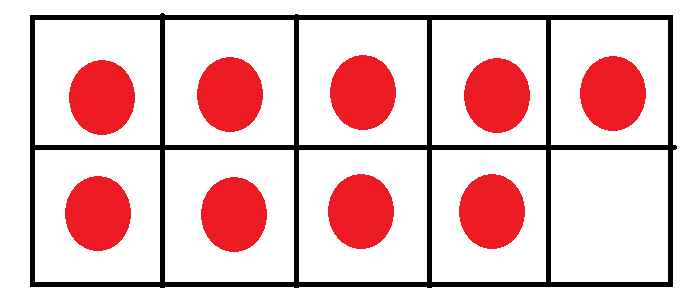
10 ( Ten )

Ten Frames for Numbers 1 to 20
Let us first understand composition of numbers from 1 to 100. Starting from 1 and by incrementing each number by 1, we can form the numbers from 1 10 100 as below –
| 1 | 10 + 1 = 11 | 20 + 1 = 21 | 30 + 1 = 31 | 40 + 1 = 41 | 50 + 1 = 51 | 60 + 1 = 61 | 70 + 1 = 71 | 80 + 1 = 81 | 9 + 1 = 91 |
| 1 + 1 = 2 | 11 + 1 = 12 | 21 + 1 = 22 | 31 + 1 = 32 | 41 + 1 = 42 | 51 + 1 = 52 | 61 + 1 = 62 | 71 + 1 = 72 | 81 + 1 = 82 | 91 + 1 = 92 |
| 2 + 1 = 3 | 12 + 1 = 13 | 22 + 1 = 23 | 32 + 1 = 33 | 42 + 1 = 43 | 52 + 1 = 53 | 62 + 1 = 63 | 72 + 1 = 73 | 82 + 1 = 83 | 92 + 1 = 93 |
| 3 + 1 = 4 | 13 + 1 = 14 | 23 + 1 = 24 | 33 + 1 = 34 | 43 + 1 = 44 | 53 + 1 = 54 | 63 + 1 = 64 | 73 + 1 = 74 | 83 + 1 = 84 | 93 + 1 = 94 |
| 4 + 1 = 5 | 14 + 1 = 15 | 24 + 1 = 25 | 34 + 1 = 35 | 44 + 1 = 45 | 54 + 1 = 55 | 64 + 1 = 65 | 74 + 1 = 75 | 84 + 1 = 85 | 94 + 1 = 95 |
| 5 + 1 = 6 | 15 + 1 = 16 | 25 + 1 = 26 | 35 + 1 = 36 | 45 + 1 = 46 | 55 + 1 = 56 | 65 + 1 = 66 | 75 + 1 = 76 | 85 + 1 = 86 | 95 + 1 = 96 |
| 6 + 1 = 7 | 16 + 1 = 17 | 26 + 1 = 27 | 36 + 1 = 37 | 46 + 1 = 47 | 56 + 1 = 57 | 66 + 1 = 67 | 76 + 1 = 77 | 86 + 1 = 87 | 96 + 1 = 97 |
| 7 + 1 = 8 | 17 + 1 = 18 | 27 + 1 = 28 | 37 + 1 = 38 | 47 + 1 = 48 | 57 + 1 = 58 | 67 + 1 = 68 | 77 + 1 = 78 | 87 + 1 = 88 | 97 + 1 = 98 |
| 8 + 1 = 9 | 18 + 1 = 19 | 28 + 1 = 29 | 38 + 1 = 39 | 48 + 1 = 49 | 58 + 1 = 59 | 68 + 1 = 69 | 78 + 1 = 79 | 88 + 1 = 89 | 98 + 1 = 99 |
| 9 + 1 = 10 | 19 + 1 = 20 | 29 + 1 = 30 | 39 + 1 = 40 | 49 + 1 = 50 | 59 + 1 = 60 | 69 + 1 = 70 | 79 + 1 = 80 | 89 + 1 = 90 | 99 + 1 = 100 |
Now, consider the below chart that displays the ten frames of numbers from 1 to 20.
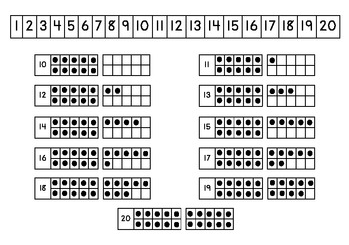
The above chart clearly demonstrates the following –
The number can be written as 10 + 0 = 1 0
The number 11 can be written as 10 + 1 = 1 1
The number 12 can be written as 10 + 2 = 1 2
The number 13 can be written as 10 + 3 = 1 3
The number 14 can be written as 10 + 4 = 1 4
The number 15 can be written as 10 + 5 = 1 5
The number 16 can be written as 10 + 6 = 1 6
The number 17 can be written as 10 + 7 = 1 7
The number 18 can be written as 10 + 8 = 1 8
The number 19 can be written as 10 + 9 = 1 9
The number 20 can be written as 10 + 10 = 2 0
In a similar manner, we can write any number using ten frames.
Addition of single digit numbers using Ten Frames
Addition, in mathematics, can be defined as the process of combining two or more numbers together to make a new total or sum.
We know that the single digit numbers are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. This is the order in which we count the numbers where 2 comes after 1, 3 comes after 2 and so on. A single – digit has the place value of a unit in the place value system of the numbers.
There can be different methods to help children understand how to add numbers. Let us discuss of these methods –
- Addition by Forward counting
- Addition using ten frames
Addition by Forward Counting
Let us consider a situation where you have 3 chocolates. Your brother gives you 4 more chocolates. How many chocolates do you have now?
In order to add 4 chocolates to the 3 chocolates that you already have, starting from 3, you will move 4 places to the right of the counting of numbers. So, 4 points after 3, in the number system is 7. Hence, 3 + 4 = 7
Addition using ten frames
We can add two or more single digit numbers using ten frames. Let us different single digit numbers and check the representation of their addition using ten frames –
1 ( One ) + 2 ( two ) = 3 ( Three )

2 ( Two ) + 3 ( Three ) = 5 ( Five )

3 ( Three ) + 5 ( Five ) = 8 ( Eight )

Addition of a Single Digit Number with a Two Digit Number
In the counting of numbers, two digit numbers start from 10. Then we have 11, 12, 13, 14, 15, ….. and so on. It is important to note here that two digit number “ab” can be written in the form 10 x a + b, where a has the ten’s place value and b has the unit value in the number system.
There can be different methods to help children understand how to add a single digit number to a two digit number. Let us discuss some of these methods –
- Addition by not carrying forward
- Addition by carrying forward
- Addition using ten frames
Addition with No Carrying Forward
For adding a Single Digit with a Two Digit Number, the digit at the one’s place value of first number will be added to the digit at the one’s place of the second number.
Let us understand it using an example.
Suppose we want to add 5 and 13.
5 – 5 is at the unit’s place in the number.
13 – 1 is the ten’s place while 3 is the unit’s place.
So, we add the unit’s digit of both the number as shown below –
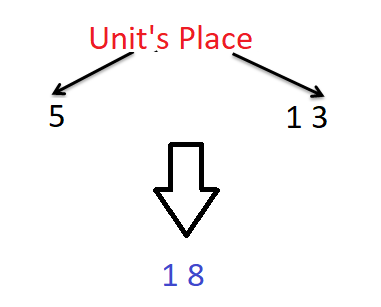
Here we can see that 5 + 3 = 8 < 10, so the result obtained was a single digit number at the unit’s place. But if we were to add the numbers 5 + 16, we would have got 5 + 6 = 11, then how would we have written 11 in the answer. This is where the concept of carrying forward comes into force.
Addition with Carrying forward
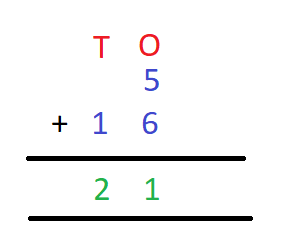
Let us consider two numbers 5 and 16. How will we add these two numbers? Let us find out.
5 = 0 tens + 5 ones
16 = 1 tens + 6 ones.
Therefore,
5 + 16 = 0 tens + 5 ones
+ 1 tens + 6 ones
1 tens + 11 ones
Now, 11 ones = 1 tens + 1 ones
Therefore, we have 5 + 16 = 1 tens +1 tens + 1 ones = 2 tens + 1 ones.
Hence, 5 + 16 = 21
Addition using Ten Frames
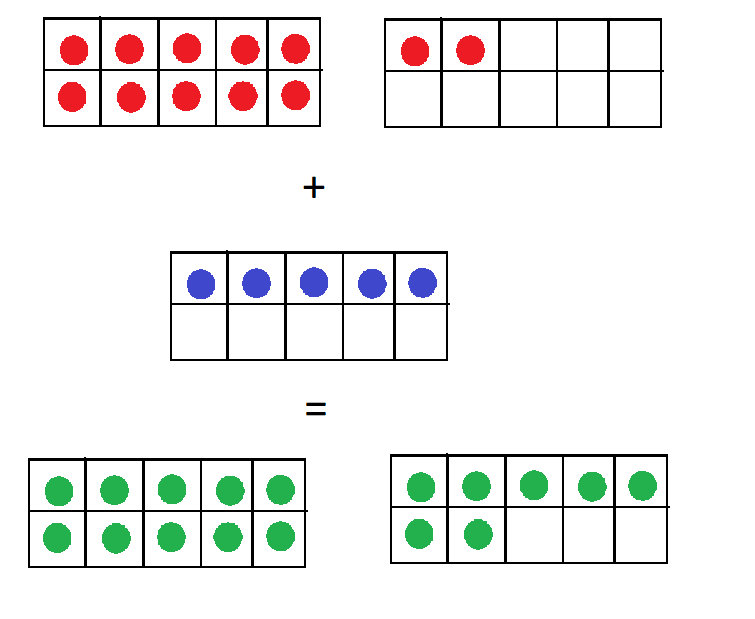
We can add a single digit number to a two digit number using ten frames. Let us consider a single and two digit numbers and check the representation of their addition using ten frames –
5 ( Five ) + 12 ( Twelve ) = 17 ( Seventeen )
Subtraction of numbers on ten frames
The process of finding the difference between two numbers is known as subtraction. In other words, it is the process of taking away a number from another. The number that is subtracted is called the subtrahend while the number from which the subtrahend is subtracted is called minuend. The result of this subtraction is called the difference.
There can be different methods to help children understand how to subtract a single digit number from a other single digit number. Let us discuss some of these methods –
- Subtraction by backward counting
- Subtraction using ten frames
Let us compare the two methods
Subtraction of single digit numbers using backward counting
Suppose we have two numbers, 3 and 9. We wish to subtract 3 from 9. The difference we get upon the subtraction is 6.
Hence 9 -3 = 6
But, what if we want to do it the other way round? That is, we wish to subtract 9 from 3. Is that possible?
Can we subtract a larger number from a smaller number? Remember the number lines about which you must have studied earlier. They have negative numbers too.
When you subtract a larger number from a smaller number, you subtract their whole values and place a sign of minus (-) against the difference.
This means that we subtract 9 from 3, we actually subtract 3 from 9, where we get the answer as 6 and place the minus sign before it, making the net answer as -6.
Hence, 3 – 9 = -6
Subtraction using ten frames
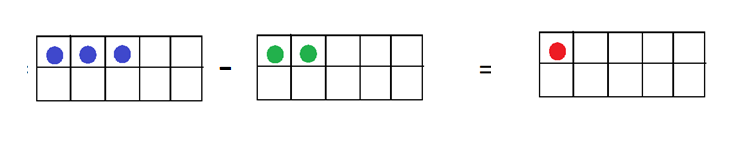
We can subtract one single digit number from another using ten frames. Let us take two single digit numbers and check the representation of their subtraction using ten frames –
3 ( Three ) = 2 ( Two ) – 1 ( One )
Using Ten Frames to understand the Place Value System
We know that place value is the basis of our entire number system. This is the system in which the position of a digit in a number determines its value. The place value of a digit in a number is the value it holds to be at the place in the number. Therefore, the number 65,471 is different from 17,645 because the digits are in different positions.
We also know that “ ten “ is the building block of our Base 10 numeration system. Ten frames help in the understanding of two digit numbers as they represent each ddigit in a different frame.
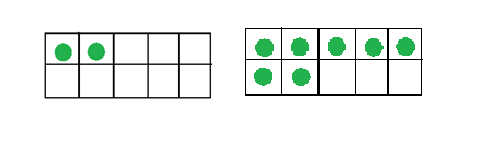
For instance, the difference between 27 and seventy two can be clearly observed in their respective ten frames.
Twenty Seven ( 2 7 )
Seventy two ( 7 2 )
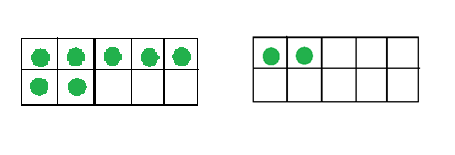
In this way, ten frames are apt for understanding the ones place and the tens place of the place value system.
Solved Examples
Example 1 Peter has 10 ten frames filled with counters. There are 100 counters in total. What number do the blue and pink counters represent respectively?
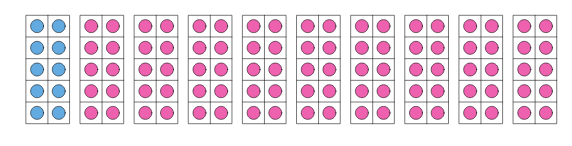
Solution We have been given the representation of 10 frames filled with counters that Peter has. We need to find the count of blue and pink counters represent respectively.
We can observe that the blue counters are filled in one block of ten frames; this means that it represents the number 10
Next, there are nine pink ten frames of pink colour, all completely filled. Therefore the number of pink counters = 10 +10 +10 + 10 +10 + 10 + 10 + 10 + 10 = 90
Hence, blue counters are 10 and pink counters are 90.
Example 2 What number do the following counters represent?
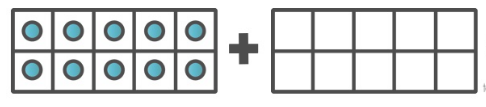
Solution We can see that the first ten frame is completely filled; hence it represents the number 10. The second ten frame is empty which means it represents the number 0. There is the sign of “ + “ between the counters which means we need to add them. Hence, we have
10 + 0 = 10
Thus, the given arrangement of counters represents the number 10
Key Facts and Summary
- Ten-Frames are two-by-five rectangular frames into which objects like counters can be placed to show numbers less than or equal to ten.
- Ten frames are often used as learning tools for numbers up to 10.
- Ten frames help with developing number sense.
- Ten frames are useful in understanding the relationships of numbers, especially for the numbers from 1 to 10.
- Ten frames help the children visualise the numbers which makes it easier for them to understand about working with numbers.
- Ten frames are useful in making the children understand the composing and decomposing of numbers.
- Addition, in mathematics, can be defined as the process of combining two or more numbers together to make a new total or sum.
- The process of finding the difference between two numbers is known as subtraction.
Recommended Worksheets
Ten Frames (Martin Luther King Day Themed) Math Worksheets
Place Value: Ten Thousand and Hundred Thousand (Chinese New Year Themed) Math Worksheets
Skip Counting (Diwali Themed) Math Worksheets









