Introduction
In arithmetic, we usually come across statements of the following type –
- 16 + 6 = 22
- 7 x ( 4 + 6 ) = 7 x 4 + 7 x 6
Such a statement involving the symbol “=” is called a statement of equality or simply an equality.
None of the above statements involves a variable.
A statement of equality that involves one or more variables is called an equation.
Consider the following statements –
- A number x increased by 7 is 15.
- 9 exceeds a number x by 3
- 4 times a number x is 24
- A number y divided by 5 is 7
- The sum of a number x and twice the number y is 12
We can write the above statements as under –
- x + 7 = 15
- 9 – x = 3
- 4x = 24
- $\frac{y}{5}$ = 7
- x + 2y = 12
Each one of the above statements is a statement of equality, containing one or more variables. Thus each one of them is an equation.
Definition of a Linear Equation
An equation in which the highest power of the variables involved is 1 is called a linear equation. In other words, a linear equation is a mathematical equation that defines a line. While each linear equation corresponds to exactly one line, each line corresponds to infinitely many equations. These equations will have a variable whose highest power is 1.
The sign of equality divides an equation into two sides, namely the left-hand side and the right-hand side, written as L.H.S and R.H.S respectively.
Linear Equations Based on the Number of Variables
We have different linear equations based on the number of variables they have. For example,
Equation with one Variable
An equation may have only one variable such as –
12x – 10 = 0
18x = 12
Equation with two Variables
An equation may have two variables, such as
12x +10y – 10 = 0
12x +23y = 20
Equation with three Variables
An equation may have three variables such as
12x +10y -3z – 10 = 0
12x +23y – 12z = 20
Similarly, there can be equations that have any number of variables. There are different methods to solve linear equations depending on the number of variables they have. Now let us see how to solve linear equations in one variable.
Solution of a Linear Equation
A number that makes L.H.S = R.H.S when it is substituted for the variable in an equation is said to satisfy the equation and is called the solution or root of an equation.
Solving Linear Equations
Before learning the methods of solving the equations, it is important to know that there are certain rules to solve equations. Let us check what these rules are –
Rules for Solving Linear Equations
The following are the rules for solving linear equations –
- We can add the same number to both sides of the equation. This means that if x + 5 = 7, then x + 5 + 2 = 7 + 2
- We can subtract the same number from both sides of the equation. This means that if x + 5 = 7 then x + 5 – 2 = 7 – 2
- We can multiply both sides of the equation by the same non-zero number. This means that if x + 5 = 4, then 6 ( x + 5 ) = 6 x 4
- We can divide both sides of the equation by the same non-zero number. This means that if 3x = 10, then $\frac{3x}{3} = \frac{10}{3}$
Let us now learn what the methods to solve linear equations are.
There are many methods of solving linear equations. Some of them are –
- Solving Equations with division
- Solving Equations with multiplication
- By trial and error method
- Transposition method
Solving Equations with division
We can use the same “do the same thing to both sides” idea that we use to solve equations with addition and subtraction to solve equations that involve multiplication and division. For this purpose, let us recall what we mean by division.
On the other hand, in the division, when we divide, we split into equal groups. For instance, 10 ÷ 5 = 2 means 10 is divided into 2 groups of 5
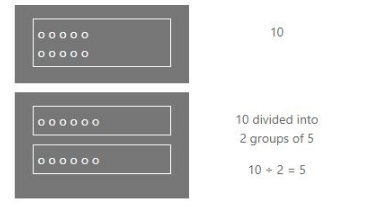
We can solve the equations below by “getting rid of” or “cancelling out” the multiplication by dividing (doing the opposite operation.)
Let us understand it using an example.
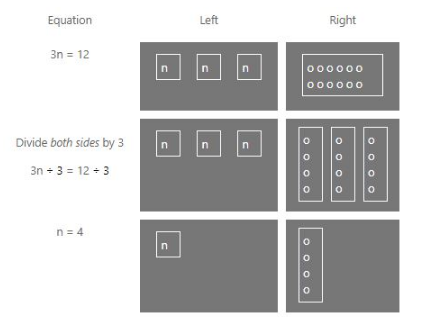
Suppose we want to solve the equation 3 n = 12
Since the coefficient of n is 3, we will divide both the sides of the equation by 3. We will get
3 n ÷ 3 = 12 ÷ 3
⇒ n = 4
Below is a graphical representation of the same for a better understanding.
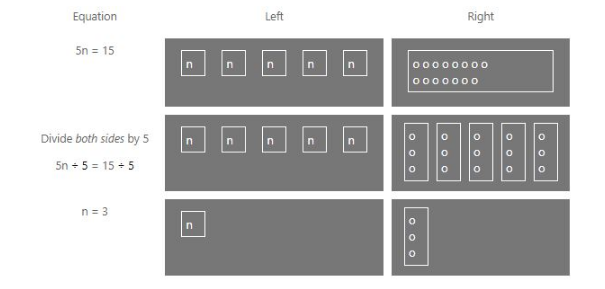
Let us take another example
Suppose we want to solve the equation 5 n = 15
Since the coefficient of n is 5, we will divide both the sides of the equation by 5. We will get
5 n ÷ 3 = 15 ÷ 5
⇒ n = 3
Below is a graphical representation of the same for a better understanding.
Solving Equations with multiplication
We can solve the equations below by “getting rid of” or “cancelling out” the division by multiplying (doing the opposite operation.) When we multiply we combine a group of equal numbers. For instance, 3 x 4 = 12 means 3 groups of 4 or 4 groups 3 which further equal 12.
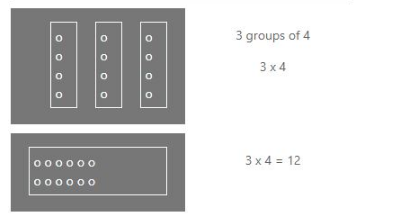
Let us understand it using an example.
Suppose we wish to solve the equation $\frac{n}{3}$ = 2
To solve this equation, w will multiply both sides by 3 to get,
$\frac{n}{3}$ x 3 = 2 x 3
⇒ n = 6
Below is a graphical representation of the same for a better understanding.
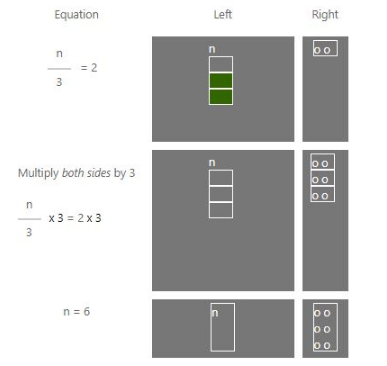
Let us take another example.
Suppose we wish to solve the equation $\frac{n}{5}$ = 4
To solve this equation, w will multiply both sides by 5 to get,
$\frac{n}{5}$ x 5 = 4 x 5
⇒ n = 20
Below is a graphical representation of the same for a better understanding.
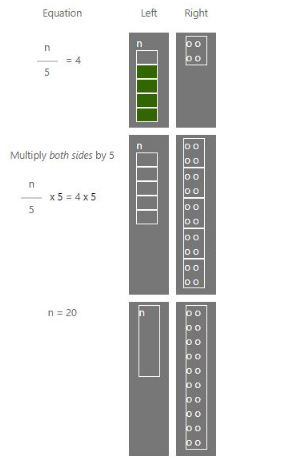
So, from above we can say that we can “get rid of” or “cancel” multiplication by dividing and we can “get rid of” or “cancel” division by multiplying.
Trial and Error method
In this method, we often make a guess of the root of the equation. We find the values of the left-hand side, L.H.S and the right-hand side, R.H.S of the given equation for different values of the variable. The value of the variable for which L.H.S = R.H.S is the root of the equation.
Let us understand the method through some examples.
Example
Solve the following equations by the trial and error method:
- x + 7 = 10
- 5x = 30
Solution
As defined in the trial and error method, we will check the values of the L.H.S and the R.H.S of the equation for some values of x and continue to do so until the L.H.S becomes equal to the R.H.S
- The given equation is x + 7 = 10
We have,
L.H.S = x + 7 and R.H.S =10
We will substitute different values of x in the L.H.S until we get the result as 10 which is our R.H.S.
The following tables shows our assumptions of trial and error –
| Value of “x” | L.H.S | R.H.S | Is L.H.S = R.H.S |
| 1 | 1 + 7 = 8 | 10 | No |
| 2 | 2 + 7 = 9 | 10 | No |
| 3 | 3 + 7 = 10 | 10 | Yes |
From the above table, we have that when x is substituted by 3, we get L.H.S = R.H.S
Hence, x = 3 is the solution for the equation, x + 7 = 10
- The given equation is 5x = 30
We have L.H.S = 5x and R.H.S = 30
We will substitute different values of x in the L.H.S until we get the result as 30 which is our R.H.S.
| Value of “x” | L.H.S | R.H.S | Is L.H.S = R.H.S |
| 1 | 5 x 1 = 5 | 30 | No |
| 2 | 5 x 2 = 10 | 30 | No |
| 3 | 5 x 3 = 15 | 30 | No |
| 4 | 5 x 4 = 20 | 30 | No |
| 5 | 5 x 5 = 25 | 30 | No |
| 6 | 5 x 6 = 30 | 30 | Yes |
From the above table, we have that when x is substituted by 6, we get L.H.S = R.H.S
Hence, x = 6 is the solution for the equation, 5x = 30
Transposition Method
By transposing a term of an equation with simply means changing its fine and carrying it to the other side of the equation any term of an equation may be taken to the other side with its sign change without affecting the equality this process is called transposition when we carry a term of an equation from L.H.S to R.H.S and R.H.S to L H.S the plus sign of the term changes into the minus sign on the other side and vice versa
The transposition method involves the following steps –
- Obtain the linear equation
- Identify the unknown quantity (variable)
- Simplify the L.H.S and R.H.S by removing grouping symbols (if any)
- Transfer all terms containing the variable on the L.H.S and constant terms on the R.H.S of the equation. Note that the size of the terms will change in carrying them from L.H.S to R.H.S and vice versa
- Simplify L.H.S and R.H.S in the simplest form so that each side contains just one term
- Solve the equation thus obtained according to the rules.
Solving Real-Life Problems using Simple Linear Equations
We shall now learn about the formulation and solution of some practical problems. These problems involve relations among unknown quantities which we call variables and known quantities which are known as numbers and are often stated in words. That is why we often refer to this problem that word problem. A word problem is first translated in the form of an equation containing unknown quantities, i.e. variable and known quantities i.e. numbers or constants and then we solve it by using any of the methods we have learnt. The procedure to translate a word problem in the form of an equation is known as the formulation of the problem. Thus the process of solving a word problem consists of two parts namely, formulation and solution
- Following steps should be followed to solve a word problem –
- Read the problem carefully and note what is given and what is required
- Denote the unknown quantity by some letters, say x, y, z, etc.
- Translate the statements of the problem into a mathematical statement
- Using the condition given in the problem, form the equation
- Solve the equation for the unknown
- Check whether the solution satisfies the equation
Let us now understand the above steps through some examples –
Example 1 The sum of two consecutive numbers is 53, find the numbers.
Solution We have been given that
The sum of two consecutive numbers is 53. We need to find the two numbers. So, going by the steps defined above, we first give a name to the unknown value which in this case is the numbers. Therefore,
Let the first number be x.
Then the next consecutive number will be x + 1
It is given that the sum of two consecutive numbers is 53, therefore, we can form an equation in the following manner –
x + ( x + 1 ) = 53
Now that we have the equation, we will solve it for x.
x + ( x + 1 ) = 53
⇒ 2x + 1 = 53
⇒ 2x = 53 – 1
⇒ 2x = 52
⇒ x= 26
Hence the first number is 26. Now since the next number is a consecutive number, the second number will be x + 1 = 27.
Therefore, the two numbers are 26 and 27
Example 2 Sara’s mother is three times as old as Sara and four times as old as Sara’s sister; Ann. Ann is three years younger than Sara. How old are Sara, Ann and their mother?
Solution We have been given that –
Sara’s mother is three times as old as Sara and four times as old as Sara’s sister; Ann. Ann is three years younger than Sara.
So, going by the steps defined above, we first give a name to the unknown value which in this case is the ages of Sara and Ann. Therefore,
Let Sara’s age be x years
It is given that Ann is three years younger than Sara.
Therefore,
Ann’s age = ( x – 3 ) years
Also, it is given that Sara’s mother is three times as old as Sara
Therefore,
Sara’s mother’s age = 3x years………………………….. (1)
Next, Sara’s mother is four times as old as Ann
Therefore,
Sara’s mother’s age = 4 ( x – 3 ) years ……………………… (2)
From (1) and (2) we have
3x = 4 ( x – 3 )
⇒ 3x = 4x – 12
⇒ 3x – 4x = -12
⇒ -x = -12
⇒ x = 12
Hence, Sara’s age is 12 years.
Now
Ann’s age = ( x – 3 ) years
Hence, Ann’s age = 12 – 3 = 9 years
Also,
Sara’s mother’s age = 3x years
Therefore,
Sara’s mother’s age = = 3 x 12 = 36 years.
Hence, Sara’s age = 12 years, Ann’s age = 9 years and Sara’s mother’s age = 36 years
Solved Examples
Example 1 Solve the following equation: 2x + 7 = 19
Solution We have been given that
2x + 7 = 19
⇒ 2x = 19 – 7
⇒ 2x = 12
⇒ x = 6
Hence x = 6 is the solution of the equation 2x + 7 = 19
Example 2 Solve the equation x -3 = 5 and check the result
Solution We have x -3 = 5
To solve this equation we have to get checked by itself on the left-hand side (L.H.S). To get x by itself on the L.H.S we need to shift -3. This can be done by adding three to both sides of the equation.
We have,
x– 3 = 5
⇒ x – 3 + 3 = 5 + 3
⇒ x + 0 = 8
⇒ x = 8
Hence, x = 8 is the solution to the equation x – 3 = 5
Now let us check the result.
Substituting x = 8 in the given equation, we have
L.H.S = x – 3 = 8 – 3 = 5
We have R.H.S = 5
Since L.H.S = R.H.S, we can say that our answer is correct.
Example 3 Solve 0.3x + 0.4 = 0.28x + 1.16
Solution We have
0.3x + 0.4 = 0.28x + 1.16
⇒ 0.3x – 0.28x = 1.16 – 0.4
⇒ ( 0.3 – 0.28 )x + 1.16 – 0.4
⇒ 0.02x = 0.76
⇒ x = $\frac{0.76}{0.02}$
⇒ x = 38
Hence, x = 38 is the solution to the problem 0.3x + 0.4 = 0.28x + 1.16
Key Facts and Summary
- A statement of equality that involves one or more variables is called an equation.
- An equation in which the highest power of the variables involved is 1 is called a linear equation.
- We have different linear equations based on the number of variables they have.
- We can add the same number to both sides of the equation. This means that if x + 5 = 7, then x + 5 + 2 = 7 + 2
- We can subtract the same number from both sides of the equation. This means that if x + 5 = 7 then x + 5 – 2 = 7 – 2
- We can multiply both sides of the equation by the same non-zero number. This means that if x + 5 = 4, then 6 ( x + 5 ) = 6 x 4
- We can divide both sides of the equation by the same non-zero number. This means that if 3x = 10, then $\frac{3x}{3} = \frac{10}{3}$
- Solving Equations with division, Solving Equations with multiplication, By trial and error method and the Transposition method are some of the methods using which we can solve simple linear equations.
Recommended Worksheets
One-Variable Equations (Employment Themed) Worksheets
Graphing Linear Equations (First African-Americans Themed) Math Worksheets
Graphing and Solving Systems of Linear Equations in Two Variables 8th Grade Math Worksheets









