Introduction
Numbers are very commonly used in our day to day life. In general, we need not state the exact number as an answer to the question which requires us to tell about how many. In other words, in order to ease our calculations, we often approximate the numbers to some extent. It helps us give approximate answers where exact values are not required. For instance, we may say that there are around 600 students in a school. That does not necessarily mean that there are exactly 600 students in a school. The exact number of students in the school may be somewhere around 600 which, for convenience, we have rounded off to 600. Rounding off is also termed as a shortcut method. Another example can be if you plan an event at home you can just estimate the number of guests that are supposed to attend the event. It can be a rough estimate of the number of people say 200. This does not mean that exactly 200 people will attend the event. This means we can round off numbers to the nearest place value, say 10, 100, 1000 etc.
But can we round off decimal numbers as well in the same manner as we do for whole numbers? Let us find out.
Before we learn about rounding off decimal numbers, it is important to recall what we mean by decimals?
What are Decimals?
Let us recall what we mean by a decimal. A decimal is another way of expressing a fraction. For example the fraction 110 in decimal form is written as 0.1. This dot between the two digits is called the decimal point. So, the decimal number 1.8 will be read as one point eight. Now, just like the place values of whole numbers such as ones, tens and hundreds, the decimal numbers also have their own place value system. This is extremely important to understand as unless we are not aware of the place of a digit in a decimal, we cannot round it off. Therefore, let us recall the place value system of decimals.
Place Value System of Decimals
We know that each place in the place value table has a value ten times the value of the next place on its right. In other words, the value of a place is one-tenth of the value of the next place on its left. We observe that if one digit moves one place left to right its value becomes one-tenth ($\frac{1}{10}$ ) of its previous value and when it moves two places left to right its value comes one-hundredth ( $\frac{1}{100}$ ) of its previous term and so on. Therefore, if we wish to move beyond ones place which is the case of decimals, we will have to extend the place value table by introducing the places of tenths ( $\frac{1}{10}$ ), hundredths ($\frac{1}{100}$ ), thousandths ( $\frac{1}{1000}$ ) and so on.
Therefore, the place value table in case of a decimal number will be of the form –
| Thousands ( 1000 ) | Hundreds ( 100 ) | Tens (10) | Ones ( 1 ) | Tenths ($\frac{1}{10}$ ) | Hundredths ( $\frac{1}{100}$ ) | Thousandths ( $\frac{1}{1000}$ ) |
For example, the decimal number 257.32 in the place value system will be written as –
| Hundreds | Tens | Ones | Tenths | Hundredths |
| 2 | 5 | 7 | 3 | 2 |
A decimal or a decimal number may contain a whole number part and a decimal part. The following table shows the whole number part and the decimal part of some decimals –
| Number | Whole Number Part | Decimal Part |
| 13.95 | 13 | 95 |
| 9.053 | 9 | 053 |
| 0.148 | 0 | 148 |
| 65.0 | 65 | 0 |
| 17 | 17 | 0 |
| 0.003 | 0 | 003 |
| 0.2 | 0 | 2 |
From the above discussion, we can see that the first three places on the right of the decimal point are tenths, hundredths and thousandths. Let us learn about rounding off decimals at these place values.
Round Off to the Nearest Tenth
Rounding off to the nearest tenth is also known as rounding off to one decimal place. So, how do we round off a number to the nearest tenth? Let us understand this by an example.
Suppose a tree is 6.84 m tall. Let us round off its height to the nearest tenth. To round off this number to the nearest tenth, let us draw a number line and show the decimals as below

In the above number line, we can see that 6.84 is closer to 6.80 than to 6.90. Hence, 6.84 will be rounded off the nearest decimal place 6.8.
However, every time we wish to round off a number we cannot draw a number to the line to check which decimal number is the given number closer to. Therefore, it is important to follow some rules for rounding off a number to the nearest tenth.
The following are the rules that must be followed for rounding off a number to the nearest tenth –
- Identify the place you want to the round to. ( In case we have the tenth place )
- Examine the digit to the right of the rounding place digit.
- If that digit is equal to 5 or greater than 5. Add 1 to the rounding place digit. If the digit is less than 5, let the rounding place digit remain as such.
- In both the cases, drop all the digits to the right of the rounding place digit.
From the above rules, we can clearly see that similar to rounding of whole numbers, there are two ways of rounding decimals to the nearest tenth –
- Rounding Up
- Rounding Down
Let us understand both the cases for rounding off to the nearest tenth.
Rounding Up
If the number at the tenth’s place is followed by 5, 6, 7, 8, or 9, the number is rounded up.
Example – We want to round off 54.89 to the nearest 10.
- Look for the digit at the ten’s place. It is 8.

- Now look for the digit to the right of the digit at the tenth’s place. The number is 9

3. Since this number is greater than 5, we round up the number, i.e. we round it off to the nearest 10 that comes next to this number. So, 9 becomes 10 which by adding to 8 at the tenth’s place, becomes 90.
Hence, the number 54.89 after being rounded off to the nearest tenth is 54.90 or 54.9.
Note: Here we moved up the number to the nearest tenth, which is why it is called rounding up.
Rounding Down
If the number at the tenth’s place is followed by 0, 1, 2, 3 or 4, the number is rounded down. Let us understand it by an example.
Suppose we want to round off the number 24.61 to the nearest tenth. We will follow the following steps –
- Look for the digit at the tenth’s place. It is 6.

- Now look for the digit to the right of the digit at the tenth’s place. The number is 1.
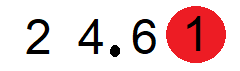
- Since this number is less than 5, we round down the number, i.e. we round it off to the nearest 10 that comes before this number. So, 1 becomes 0 which by adding to 6 at the tenth’s place, becomes 60.
- Hence, the number 24.61 after being rounded off to the nearest tenth is 24.60 or 24.6
Note: Here we moved down the number to the nearest tenth, which is why it is called rounding down.
Now, that we have understood how to round off a decimal to the tenth’s place, let us now learn how to round off a decimal to the hundredth place.
Round Off to the Nearest Hundredth
Rounding off to the nearest hundredth is also known as rounding off to two decimal places. This is the most common form of rounding off that we use in solving everyday problems, especially when related to money. So, how do we round off a number to the nearest hundredth? Let us understand this by an example.
The following are the rules that must be followed for rounding off a number to the nearest hundredth –
- Identify the place you want to the round to. ( In case we have the hundredths place )
- Examine the digit to the right of the rounding place digit.
- If that digit is equal to 5 or greater than 5. Add 1 to the rounding place digit. If the digit is less than 5, let the rounding place digit remain as such.
- In both the cases, drop all the digits to the right of the rounding place digit.
From the above rules, we can clearly see that similar to rounding of whole numbers, there are two ways of rounding decimals to the nearest hundredth –
- Rounding Up
- Rounding Down
Let us understand both the cases for rounding off to the nearest hundredth.
Rounding Up
If the number at the hundredth place is followed by 5, 6, 7, 8, or 9, the number is rounded up.
Example – We want to round off 54.689 to the nearest 10.
- Look for the digit at the hundredth’s place. It is 8.

- Now look for the digit to the right of the digit at the thousandth’s place. The number is 9
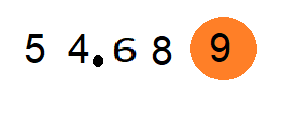
3. Since this number is greater than 5, we round up the number, i.e. we round it off to the nearest 10 that comes next to this number. So, 9 becomes 10 which by adding to 8 at the hundredth’s place, becomes 90.
Hence, the number 54.689 after being rounded off to the nearest hundredth is 54.690 or 54.69.
Note: Here we moved up the number to the nearest hundredths, which is why it is called rounding up.
Rounding Down
If the number at the hundredth’s place is followed by 0, 1, 2, 3 or 4, the number is rounded up. Let us understand it by an example.
Suppose we want to round off the number 24.361 to the nearest tenth. We will follow the following steps –
- Look for the digit at the hundredth’s place. It is 6.
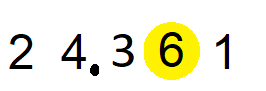
- Now look for the digit to the right of the digit at the hundredth’s place. The number is 1.
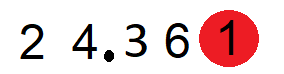
- Since this number is less than 5, we round down the number, i.e. we round it off to the nearest 10 that comes before this number. So, 1 becomes 0 which by adding to 6 at the hundredth place, becomes 60.
- Hence, the number 24.361 after being rounded off to the nearest hundredth is 24.360 or 24.36
Note: Here we moved down the number to the nearest hundredths, which is why it is called rounding down.
Now, that we have understood how to round off a decimal to the hundredth place, let us now learn how to round off a decimal to the thousandth’s place.
Round Off to the Nearest Thousandth
Rounding off to the nearest thousandth is also known as rounding off to three decimal places. So, how do we round off a number to the nearest thousandth? Let us understand this by an example.
The following are the rules that must be followed for rounding off a number to the nearest thousandth –
- Identify the place you want to the round to. ( In case we have the thousandth place )
- Examine the digit to the right of the rounding place digit.
- If that digit is equal to 5 or greater than 5. Add 1 to the rounding place digit. If the digit is less than 5, let the rounding place digit remain as such.
- In both the cases, drop all the digits to the right of the rounding place digit.
From the above rules, we can clearly see that similar to rounding of whole numbers, there are two ways of rounding decimals to the nearest thousandth –
- Rounding Up
- Rounding Down
Let us understand both the cases for rounding off to the nearest thousandth.
Rounding Up
If the number at the thousandth place is followed by 5, 6, 7, 8, or 9, the number is rounded up.
Example – We want to round off 54.1689 to the nearest 10.
- Look for the digit at the thousandth place. It is 8.
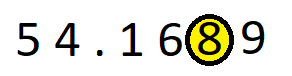
- Now look for the digit to the right of the digit at the thousandth’s place. The number is 9
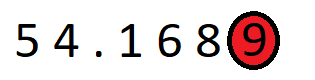
3. Since this number is greater than 5, we round up the number, i.e. we round it off to the nearest 10 that comes next to this number. So, 9 becomes 10 which by adding to 8 at the thousandth’s place, becomes 90.
Hence, the number 54.1689 after being rounded off to the nearest hundredth is 54.169 or 54.169.
Note: Here we moved up the number to the nearest thousandths, which is why it is called rounding up.
Rounding Down
If the number at the thousandth’s place is followed by 0, 1, 2, 3 or 4, the number is rounded up. Let us understand it by an example.
Suppose we want to round off the number 24.5163 to the nearest tenth. We will follow the following steps –
- Look for the digit at the thousandth’s place. It is 6.
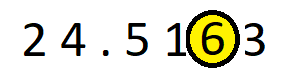
- Now look for the digit to the right of the digit at the thousandth’s place. The number is 3.
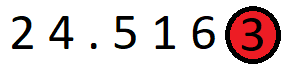
- Since this number is less than 5, we round down the number, i.e. we round it off to the nearest 10 that comes before this number. So, 1 becomes 0 which by adding to 6 at the thousandth’s place, becomes 60.
- Hence, the number 24.5163 after being rounded off to the nearest thousandths is 24.516 or 24.516
Note: Here we moved down the number to the nearest thousandths, which is why it is called rounding down.
Solved Examples
Example 1 Round off 17.3829 to the nearest hundredth
Solution We have been given the number 17.3829. we need to round off this number to the nearest hundredth.
From the steps above we can see that the digit to the right of the digit at the hundredth’s place is 2 which is less than 5. Hence we will round it down to 0 which on adding to 8 at the hundredths place become 80.
Hence, 17.3829 on rounding off the nearest hundredth is 17.380
Example 2 Round off 19.83 to the nearest tenth
Solution We have been given the number 19.83. We need to round off this number to the nearest tenth.
From the steps above we can see that the digit to the right of the digit at the tenths place is 3 which is less than 5. Hence we will round it down to 0 which on adding to 3 at the tenth place become 30.
Hence, 19.83 on rounding off the nearest hundredth is 19.80 or 19.8.
Example 3 Round off 23.8254 to the nearest thousandth
Solution We have been given the number 23.8254. We need to round off this number to the nearest thousandth.
From the steps above we can see that the digit to the right of the digit at the thousandth place is 4 which is less than 5. Hence we will round it down to 0 which on adding to 5 at the thousandth place become 50.
Hence, 23.8254 on rounding off the nearest thousandth is 23.825
Key Facts and Summary
- A decimal is another way of expressing a fraction.
- Rounding off to the nearest tenth is also known as rounding off to one decimal place.
- If the number at the tenth place is followed by 5, 6, 7, 8, or 9, the number is rounded up.
- If the number at the hundredth’s place is followed by 0, 1, 2, 3 or 4, the number is rounded up.
- Rounding off to the nearest tenth is also known as rounding off to two decimal places.
- Rounding off to the nearest thousandth is also known as rounding off to three decimal places.
Recommended Worksheets
Rounding Decimals (Adventure Themed) Worksheets
Rounding Whole Numbers and Decimals (Basketball Themed) Worksheets
Rounding Off Decimals Up To Thousandths 5th Grade Math Worksheets









