Introduction
The word decimal comes from the Latin word “Decem” meaning 10. . In algebra, a decimal number can be defined as a number whose complete part and the fractional part are separated by a decimal point. Before we learn what we mean by a tenth of decimal it is important to recall the place value system of decimals that defines the position of a tenth in a decimal number.
What are Thousandths in a Decimal?
If an object is divided into 1000 equal parts, then each part is one-thousandth of the whole. This means that –
One thousandth = $\frac{1}{1000}$ which in decimal form is equal to 0.001
If we take 7 parts out of 1000 equal parts of an object, then 7 parts make $\frac{7}{1000}$ of the whole and it is written as 0.007.
Similarly, we have,
$\frac{15}{1000}$ = 0.015
$\frac{131}{1000}$ = 0.131
$\frac{974}{1000}$ = 0.974
$\frac{1265}{1000} = \frac{1000+265}{1000} = \frac{1000}{1000} + \frac{265}{1000} = 1 + 0.265 = 1.265$
$\frac{11345}{1000} = \frac{11000+345}{1000} = \frac{11000}{1000} + \frac{345}{1000} = 11 + 0.345 = 11.345$ and so on.
So, how do we obtain the thousandth of a decimal?
The following points need to be considered while writing a thousandth of a decimal number –
- A fraction of the form $\frac{Number}{1000}$ is written as a decimal obtained by putting decimal point by leaving three right most digits.
- If the number is short of digits, we insert zeros at the left of the number.
Now, let us learn about the placement of the thousandths of a decimal in the Place Value System. But before that, we must recall what we mean by the place value system of decimals.
Place Value System of Decimals
We know that each place in the place value table has a value ten times the value of the next place on its right. In other words, the value of a place is one-tenth of the value of the next place on its left. We observe that if one digit moves one place left to right its value becomes one-tenth ($\frac{1}{10}$ ) of its previous value and when it moves two places left to right its value comes one-hundredth ( $\frac{1}{100}$ ) of its previous term and so on. Therefore, if we wish to move beyond ones place which is the case of decimals, we will have to extend the place value table by introducing the places of tenths ($\frac{1}{10}$ ), hundredths ($\frac{1}{100}$ ), thousandths ( $\frac{1}{1000}$ ) and so on.
Therefore, the place value table in case of a decimal number will be of the form –
| Thousands ( 1000 ) | Hundreds ( 100 ) | Tens (10) | Ones ( 1 ) | Tenths ($\frac{1}{10}$) | Hundredths ( $\frac{1}{100}$ ) | Thousandths ( $\frac{1}{1000}$ ) |
For example, the decimal number 257.32 in the place value system will be written as –
| Hundreds | Tens | Ones | Tenths | Hundredths |
| 2 | 5 | 7 | 3 | 2 |
A decimal or a decimal number may contain a whole number part and a decimal part. The following table shows the whole number part and the decimal part of some decimals –
| Number | Whole Number Part | Decimal Part |
| 13.95 | 13 | 95 |
| 9.053 | 9 | 053 |
| 0.148 | 0 | 148 |
| 65.0 | 65 | 0 |
| 17 | 17 | 0 |
| 0.003 | 0 | 003 |
| 0.2 | 0 | 2 |
Now, how do we read the decimals using the place value system? Let us find out.
Reading the Decimal Numbers using the Place Value System
In order to read decimals, the following steps are used –
- Read the whole number part
- Read the decimal point as point
- Read the number to the right of the decimal point. For example, 14.35 will be read as Fourteen point three five. Alternatively, the number to the right of the decimal point can also be read by reading the number to the right of the decimal point and naming the place value of the last digit. For instance, the number 8.527 can also be read as eight and five hundred twenty seven thousandths.
Now let us see how to read and write the thousandths of a decimal in the Place Value System.
Thousandths of a decimal in the Place Value System
From the place value table above, we can see that the thousandth of a decimal is placed at the third digit to the right of the decimal point. Therefore, this is the position of the thousandth in the place value system. Let us understand the thousandth position of some numbers as an example.
Suppose we have the following numbers and we want to identify the digit at the thousandth place in these numbers.
- 12.6587
- 0.02369
- 1.001127
Let us check these numbers one by one.
- We have the number 12.6587. Check the digit at the third position from the right of the decimal. The number is 8. This is the thousandth place of the number having the place value 0.008.
- Next, we have the number 0.02369. Check the digit at the third position from the right of the decimal. The number is 3. This is the thousandth place of the number having the place value 0.003.
- Now, we have the number 1.00127. Check the digit at the third position from the right of the decimal. The number is 1. This is the thousandth place of the number having the place value 0.001.
Now, let us understand the representation of the thousandth of a decimal on a number line.
Representation of Thousandths of a decimal on a Number Line
Before we learn how to represent a tenth on a number let us recall what we understand by the term number line.
What is a number line?
A number line is a straight horizontal line with numbers placed at even intervals that provides a visual representation of numbers. Primary operations such as addition, subtraction, multiplication, and division can all be performed on a number line. The numbers increase as we move towards the right side of a number line while they decrease as we move left.
Representation of a Thousandth on a Number Line

Above is a visual representation of a standard number line. As is clearly visible, as we move from left to right, there is an increase in the value of numbers while it decreases when we move from right to left.
We already know how to represent fractions on a number line. Let us now represent the thousandths of a decimal on a number line. We can understand this by an example.
To represent 7.4 on a number line, we first draw 10 lines dividing the total distance between 7 and 8 into 10 equal parts.
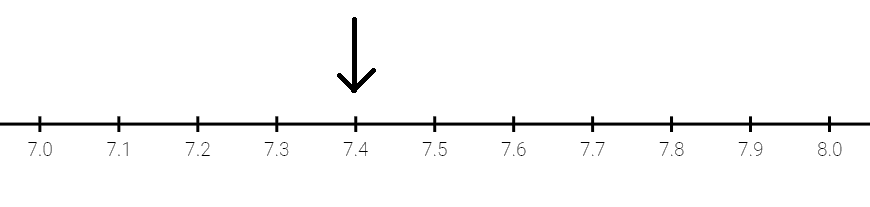
We can see that the arrow is four parts to the right of the whole number 7.
Similarly, to represent 7.45 on a number line, we first draw 10 lines dividing the total distance between 7.4 and 7.5 into 10 equal parts.

We can see that the arrow is five parts to the right of the decimal number 7.40.
Next, to represent 7.456 on a number line, we first draw 10 lines dividing the total distance between 7.45 and 7.46 into 10 equal parts.
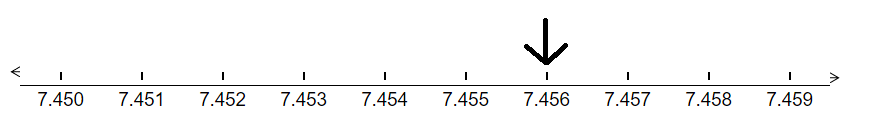
We can see that the arrow is six parts to the right of the decimal number 7.45
So, in this manner, we have represented the number 7.456 on the number line.
The steps that we used above to represent a tenth on a number line can be summarised as –
- We draw a number line between 0 and 1.
- We then draw 10 lines dividing the total distance between 0 and 1 into 10 equal parts.
- Now, one whole divided into 10 parts is equal to $\frac{1}{10}$.
- $\frac{1}{10}$ in decimal form is equal to 0.1.
- At each new line, we are adding $\frac{1}{10}$ or 0.1.
- So, between 0 and 1 we have, 0 . 1 , 0 . 2 , . 0 . 3 , 0 . 4 , 0 . 5 , 0 . 6 , 0 . 7 , 0 . 8 and 0 . 9. Similarly, between 1 and 2 we have, 1 . 1 , 1 . 2 , 1 . 3 , 1 . 4 , 1 . 5 , 1 . 6 , 1 . 7 , 1 . 8 and 1 . 9.
- We can also say that the line representing $\frac{1}{2}$ or 0.5 is the half way mark between 0 and 1. Similarly, the line representing $1\frac{5}{10}$ or 1.5 is the half way mark between 1 and 2.
- Ten tenths is equal to one whole.
- Next, we perform the same steps to draw 10 lines dividing the total distance between 0.01 and 0.02 into 10 equal parts.
- Again, we perform the same steps to draw 10 lines dividing the total distance between 0.001 and 0.002 into 10 equal parts.
- In this manner, we can plot the thousandth of a decimal on a number line.
The above process can be defined as – “To represent a thousandth on a number line, we will first have to divide the distance between two whole numbers into 10 equal parts to get their tenths values. Next, we divide again the distance between two tenths to get their hundredths values. Finally, we divide the distance between two hundredths into 10 equal parts to get their thousandths values.”
Now let us go through some solved examples on the thousandth of a decimal.
Solved Examples
Example 1 Write each of the following decimals in words
- 8.005
- 0.635
- 250.005
- 0.705
Solution We have been given four decimal numbers and we need to write them in words. Let us do them one by one.
- 8.005
We can see that the given decimal number has 3 digits on the right of the decimal point. Therefore, we will have to read the given decimal number until its thousandth part.
The number in words will be written as –
“Eight point zero zero five”. Another way to read the given decimal number is
“Eight and Five Thousandth”
Therefore, 8.005 in words will be “Eight point zero zero five” or “Eight and Five Thousandth”
- 0.635
We can see that the given decimal number has 3 digits on the right of the decimal point. Therefore, we will have to read the given decimal number until its thousandth part.
The number in words will be written as –
“Zero point six three five”. Another way to read the given decimal number is
“Zero and Six Hundred and thirty five thousandth”
Therefore, 0.635 in words will be “Zero point six three five” or “Zero and Six Hundred and thirty five thousandth”
- 250.005
We can see that the given decimal number has 3 digits on the right of the decimal point. Therefore, we will have to read the given decimal number until its thousandth part.
The number in words will be written as –
“Two hundred and fifty point zero zero five”. Another way to read the given decimal number is
“Two hundred and fifty and five thousandth”
Therefore, 250.005 in words will be “Two hundred and fifty point zero zero five” or “Two hundred and fifty and five thousandth”.
- 0.705
We can see that the given decimal number has 3 digits on the right of the decimal point. Therefore, we will have to read the given decimal number until its thousandth part.
The number in words will be written as –
“Zero point seven zero five”. Another way to read the given decimal number is
“Zero and seven hundred and five thousandth”
Therefore, 250.005 in words will be “Zero point seven zero five” or “Zero and seven hundred and five thousandth”.
Example 2 Write each of the following as a decimal number
- $7 + \frac{2}{10} + \frac{8}{100} + \frac{6}{1000}$
- $\frac{3}{100} + \frac{7}{1000}$
- $\frac{2}{10} + \frac{3}{100} + \frac{7}{1000}$
Solution We have been given three values in the fractional form and we need to write their equivalent decimal form. Let us do them one by one.
- $7 + \frac{2}{10} + \frac{8}{100} + \frac{6}{1000}$
We can see that the given fraction has one whole number and three fractional parts. Each one of the given fractional values will be needed to be converted into the corresponding decimal value to get the desired number. So, we have.
7 is a whole number so we need not change into any other form.
We know that $\frac{2}{10}$ = 0.2 and is called two tenths or 2 tenths.
Similarly, $\frac{8}{100}$ = 0.08 and is called eight hundredths or 8 hundredths
Also, $\frac{6}{1000}$ = 0.006 and is called six thousandths or 6 thousandths
Therefore, the give fraction in the decimal form will be
$7 + \frac{2}{10} + \frac{8}{100} + \frac{6}{1000}$ = 7 + 0.2 + 0.08 + 0.006 = 7.286
- $\frac{3}{100} + \frac{7}{1000}$
We can see that the given fraction has no whole number and two fractional parts. Also, it is important to see that that there is no value corresponding to one-tenth of a decimal. Each one of the given fractional values will be needed to be converted into the corresponding decimal value to get the desired number. So, we have.
We will place a 0 for a whole number as there is no whole number value in the given fraction.
Similarly, we will place a 0 for the tenth of a decimal number as there is no value corresponding to one-tenth of a decimal.
Now, $\frac{3}{100}$ = 0.03 and is called three hundredths or 3 hundredths
Also, $\frac{7}{1000}$ = 0.007 and is called seven thousandths or 7 thousandths
Therefore, the given fraction in the decimal form will be
$\frac{3}{100}$ + $\frac{7}{1000}$ = 0 + 0.0 + 0.03 + 0.007 = 0.037
- $\frac{2}{10}$ + $\frac{3}{100}$ + $\frac{7}{1000}$
We can see that the given fraction has no whole number and two fractional parts. Each one of the given fractional values will be needed to be converted into the corresponding decimal value to get the desired number. So, we have.
We will place a 0 for a whole number as there is no whole number value in the given fraction.
We know that $\frac{2}{10}$ = 0.2 and is called two tenths or 2 tenths.
Now, $\frac{3}{100}$ = 0.03 and is called three hundredths or 3 hundredths
Also, $\frac{7}{1000}$ = 0.007 and is called seven thousandths or 7 thousandths
Therefore, the given fraction in the decimal form will be
$\frac{2}{10}$ + $\frac{3}{100}$ + $\frac{7}{1000}$ = 0.2 + 0.03 + 0.007 = 0.237
Key Facts and Summary
- A decimal number can be defined as a number whose complete part and the fractional part are separated by a decimal point.
- The Place Value System is the system in which the position of a digit in a number determines its value. The place value of a digit in a number is the value it holds to be at the place in the number.
- In order to read decimals, we first
- Read the whole number part
- Read the decimal point as a point.
- If an object is divided into 1000 equal parts each part is one thousandth of the whole.
- One thousandth = $\frac{1}{1000}$ which in decimal form is equal to 0.001
- A number line is a straight horizontal line with numbers placed at even intervals that provides a visual representation of numbers. Primary operations such as addition, subtraction, multiplication, and division can all be performed on a number line.
- To represent a thousandth on a number line, we will first have to divide the distance between two whole numbers into 10 equal parts to get their tenth values. Next, we divide again the distance between two tenths to get their hundredths values. Finally, we divide the distance between two hundredths into 10 equal parts to get their thousandths values.
Recommended Worksheets
Decimals in a Number Line (Birthday Themed) Worksheets
Converting Fractions to Decimals (Winter Themed) Worksheets
Comparing Decimals (International Day of Education Themed) Worksheets









