Definition
Decimal numbers are used in many situations where accuracy is important. For example, in dealing with money, time, length, etc.
One of the applications of decimal numbers is in the business sector where money is used. When you buy at the grocery stores, most of the prices have decimals. When you spend or save money, knowledge of decimal numbers matters.
Multiplying with decimals may sound intimidating or tricky but it is like multiplying whole numbers and dealing with decimals properly.
Here are the steps to follow in multiplying with decimals.
Steps in Multiplying with Decimals
Step 1: Arrange the given numbers such that one number is above the other number.
Step 2: Ignore the decimal points and multiply the numbers as whole numbers.
Step 3: Add the results together.
Step 4. Count the number of decimal places in the given numbers.
Step 5: Place a decimal point in the answer such that it has the same decimal places in the given numbers.
Multiplying Whole Numbers by Decimals
Multiplying whole numbers by 1-digit decimals
When a decimal has a non-zero digit in the tenths place but no other non-zero digits to the right, it is said to be a 1-digit decimal. Some examples of 1-digit decimals are 0.1, 1.2, 43.6, 89.5, and 24. 7.
Let us follow the steps in multiplying with decimals by getting the product of 542 and 1.2.
Step 1: Arrange the given numbers such that one number is above the other number.
542 is the multiplicand while 1.2 is the multiplier.
542
1.2
—–
Step 2: Ignore the decimal points and multiply the numbers as whole numbers.
542 × 2 = 1084 542 × 1 = 542
5 4 2
1 . 2
——
1 0 8 4
5 4 2
Step 3: Add the results together.
5 4 2
1 . 2
——-
1 0 8 4
5 4 2
——–
6 5 0 4
Step 4. Count the number of decimal places in the given numbers.
The encircled number shows that there is just one number at the right of the decimal point.
5 4 2
1 . 2
——-
1 0 8 4
5 4 2
——–
6 5 0 4
Step 5: Place a decimal point in the answer such that it has the same decimal places in the given numbers.
The decimal point must be placed between 0 and 4. Since we only need 1 decimal place, only the number 4 is at the right of the decimal point.
5 4 2
1 . 2
——-
1 0 8 4
5 4 2
——–
6 5 0. 4
Therefore, 650.4 is the product of 542 and 1.2.
Multiplying whole numbers by 2-digit decimals
2-digit decimals are decimals having two decimal digits (tenths and hundredths). Examples of 2-digit decimals are 1.12, 4.23, 3.26, 8.95, 1224.85.
Let us multiply 1256 by 3.41.
Step 1: Arrange the given numbers such that one number is above the other number.
The multiplicand is 1256 while the multiplier is 3.41.
1 2 5 6
3. 41
——–
Step 2: Ignore the decimal points and multiply the numbers as whole numbers.
1256 × 1 = 1256 1256 × 4=5042 1256×3 = 3768
1 2 5 6
3. 41
——–
1 2 5 6
5 0 2 4
3 7 6 8
Step 3: Add the results together.
1 2 5 6
3. 41
——–
1 2 5 6
5 0 2 4
3 7 6 8
————-
4 2 8 2 9 6
Step 4: Count the number of decimal places in the given numbers.
The encircled numbers show that there are two numbers at the right of the decimal point.
1 2 5 6
3. 41
——–
1 2 5 6
5 0 2 4
3 7 6 8
————-
4 2 8 2 9 6
Step 5: Place a decimal point in the answer such that it has the same decimal places in the given numbers.
The decimal point must be placed between 0 and 4. Since we only need 1 decimal place, only the number 4 is at the right of the decimal point.
1 2 5 6
3. 41
——–
1 2 5 6
5 0 2 4
3 7 6 8
————-
4 2 8 2 . 9 6
Thus, 1256 × 3.41 = 4282.96 .
Multiplying whole numbers by 3-digit decimals
3-digit decimals are decimal numbers having three decimal digits (tenths, hundredths, and thousandths). Some examples of 3-digit decimals are 6.125, 14.243, 13.126, 88.959, 1224.107.
Given: 8052 × 1. 783
Step 1: Arrange the given numbers such that one number is above the other number.
The multiplicand is 8052 and the multiplier is 1.783.
8 0 5 2
1.7 8 3
——–
Step 2: Ignore the decimal points and multiply the numbers as whole numbers.
8052 × 3 = 24156 8052 × 8 = 64416 8052 × 7 = 56364 8052 × 1 = 8052
8 0 5 2
1.7 8 3
–——–
2 4 1 5 6
6 4 4 1 6
5 6 3 6 4
8 0 5 2
Step 3: Add the results together.
8 0 5 2
1.7 8 3
–——–
2 4 1 5 6
6 4 4 1 6
5 6 3 6 4
8 0 5 2
——————
1 4 3 5 6 7 1 6
Step 4: Count the number of decimal places.
The re are three numbers to the right of the decimal point.
8 0 5 2
1.7 8 3
–——–
2 4 1 5 6
6 4 4 1 6
5 6 3 6 4
8 0 5 2
——————
1 4 3 5 6 7 1 6
Step 5: Place a decimal point in the answer such that it has the same decimal places in the given numbers.
The decimal point must be placed between 6 and 7 since we need three decimal places.
8 0 5 2
1.7 8 3
–——–
2 4 1 5 6
6 4 4 1 6
5 6 3 6 4
8 0 5 2
——————
1 4 3 5 6 . 7 1 6
Hence, 8052 × 1.783 = 14356.716.
Multiplying Decimals by Decimals
Example 1: Multiply 1.15 by 2.34.
Step 1: Arrange the given numbers such that one number is above the other number.
1.15 is the multiplicand and 2.34 is the multiplier.
1. 1 5
2. 3 4
——-
Step 2: Ignore the decimal points and multiply the numbers as whole numbers.
115 × 4 = 460 115 × 3 = 345 115 × 2 = 230
1. 1 5
2. 3 4
——-
4 6 0
3 4 5
2 3 0
Step 3: Add the results together.
1. 1 5
2. 3 4
——-
4 6 0
3 4 5
2 3 0
————
2 6 9 1 0
Step 4: Count the number of decimal places.
There are four decimal places in the given number (.15 and .34).
1. 1 5
2. 3 4
——-
4 6 0
3 4 5
2 3 0
————
2 6 9 1 0
Step 5: Place a decimal point in the answer such that it has the same decimal places in the given numbers.
The decimal point must be placed between 2 and 6 since there should be four decimal places in the final answer.
1. 1 5
2. 3 4
——-
4 6 0
3 4 5
2 3 0
————
2 . 6 9 1 0
Thus, the product of 1.15 and 2.34 is 2.6910 or simply 2.691.
Example 2: Find the product 56.347 and 12.89.
Step 1: Arrange the given numbers such that one number is above the other number.
56. 347 is the multiplicand and 12.89 is the multiplier.
5 6. 3 4 7
1 2. 8 9
———–
Step 2: Ignore the decimal points and multiply the numbers as whole numbers.
56347 × 9 =507123 56347 × 8 =450776
56347 × 2 =112694 56347 × 1 =56347
5 6. 3 4 7
1 2. 8 9
———–
5 0 7 1 2 3
4 5 0 7 7 6
1 1 2 6 9 4
5 6 3 4 7
Step 3: Add the results together.
5 6. 3 4 7
1 2. 8 9
———–
5 0 7 1 2 3
4 5 0 7 7 6
1 1 2 6 9 4
5 6 3 4 7
————–
7 2 6 3 1 2 8 3
Step 4: Count the number of decimal places in the given numbers.
There are five numbers at the right of the decimal point in the given numbers.
5 6. 3 4 7
1 2. 8 9
———–
5 0 7 1 2 3
4 5 0 7 7 6
1 1 2 6 9 4
5 6 3 4 7
————–
7 2 6 3 1 2 8 3
Step 5: Place a decimal point in the answer such that it has the same decimal places in the given numbers.
The decimal point must be in between the digits 6 and 3.
5 6. 3 4 7
1 2. 8 9
———–
5 0 7 1 2 3
4 5 0 7 7 6
1 1 2 6 9 4
5 6 3 4 7
————–
7 2 . 6 3 1 2 8 3
Therefore, the product of 56.347 and 12.89 is 726. 31283.
Example 3: 689.357 × 12.074.
Step 1: Arrange the given numbers such that one number is above the other number.
689.357 is the multiplicand and 12.074 is the multiplier.
6 8 9.3 5 7
1 2.0 7 4
————-
Step 2: Ignore the decimal points and multiply the numbers as whole numbers.
689357× 4 = 2757428 689357× 7 = 4825499 689357× 0 = 0 689357× 2 = 1378714 689357× 1 = 689357
6 8 9.3 5 7
1 2.0 7 4
————-
2 7 5 7 4 2 8
4 8 2 5 4 9 9
0 0 0 0 0 0
1 3 7 8 7 1 4
6 8 9 3 5 7
Step 3: Add the results together.
6 8 9.3 5 7
1 2.0 7 4
————-
2 7 5 7 4 2 8
4 8 2 5 4 9 9
0 0 0 0 0 0
1 3 7 8 7 1 4
6 8 9 3 5 7
————————
8 3 2 3 2 9 6 4 1 8
Step 4: Count the number of decimal places.
There are six numbers at the right of the decimal point in the given numbers.
6 8 9.3 5 7
1 2.0 7 4
————-
2 7 5 7 4 2 8
4 8 2 5 4 9 9
0 0 0 0 0 0
1 3 7 8 7 1 4
6 8 9 3 5 7
————————
8 3 2 3 2 9 6 4 1 8
Step 5: Place a decimal point in the answer such that it has the same decimal places in the given numbers.
The decimal point must be in between the digits 6 and 3.
6 8 9.3 5 7
1 2.0 7 4
————-
2 7 5 7 4 2 8
4 8 2 5 4 9 9
0 0 0 0 0 0
1 3 7 8 7 1 4
6 8 9 3 5 7
————————
8 3 2 3 . 2 9 6 4 1 8
Hence, 689.357 × 12.074 = 8323.296418.
Example 4: 721.231 × 43.852.
Step 1: Arrange the given numbers such that one number is above the other number.
721.231 is the multiplicand and 43.852 is the multiplier.
7 2 1. 2 3 1
4 3 .8 5 2
————-
Step 2: Ignore the decimal points and multiply the numbers as whole numbers.
721231 × 2 = 1442462 721231 × 5 = 3606155 721231× 8 = 5769848 721231× 4 = 2884924
7 2 1.2 3 1
4 3.8 5 2
————–
1 4 4 2 4 6 2
3 6 0 6 1 5 5
5 7 6 9 8 4 8
2 1 6 3 6 9 3
2 8 8 4 9 2 4
Step 3: Add the results together.
7 2 1.2 3 1
4 3.8 5 2
————–
1 4 4 2 4 6 2
3 6 0 6 1 5 5
5 7 6 9 8 4 8
2 1 6 3 6 9 3
2 8 8 4 9 2 4
————————
3 1 6 2 7 4 2 1 8 1 2
Step 4: Count the number of decimal places in the given numbers.
7 2 1.2 3 1
4 3.8 5 2
————–
1 4 4 2 4 6 2
3 6 0 6 1 5 5
5 7 6 9 8 4 8
2 1 6 3 6 9 3
2 8 8 4 9 2 4
————————
3 1 6 2 7 4 2 1 8 1 2
Step 5: Place a decimal point in the answer such that it has the same decimal places in the given numbers.
The decimal point must be in between the digits 7 and 4.
7 2 1.2 3 1
4 3.8 5 2
————–
1 4 4 2 4 6 2
3 6 0 6 1 5 5
5 7 6 9 8 4 8
2 1 6 3 6 9 3
2 8 8 4 9 2 4
————————
3 1 6 2 7 . 4 2 1 8 1 2
Hence, 721.231 × 43.852 = 31627.421812.
Multiplying decimals by 10, 100 and 1000
Let us recall multiplying whole numbers by 10, 100, and 1000. Say for example we have,
75 × 10 = 750
56 × 100 = 5600
89 × 1000 = 89000
Notice that we are just adding if we are multiplying a number by ten, we are adding one zero to the number, if by 100 we are adding two zeroes, and if by 1000 we are adding three zeroes.
The same thing happens also in multiplying decimals by 10, 100, or 1000.
75, 56, and 89 can be written as 75.0, 56.00, and 89.000 in decimal, respectively.
As such, if we multiply,
75.0 × 10 = 750
56.00 × 100 = 5600
89.000 × 1000 = 89000.
If we are multiplying decimals by 10, the decimal point moves 1 place to the right.
If we are multiplying decimals by 100, the decimal point moves 2 places to the right.
If we are multiplying decimals by 1000, the decimal point moves 3 places to the right.
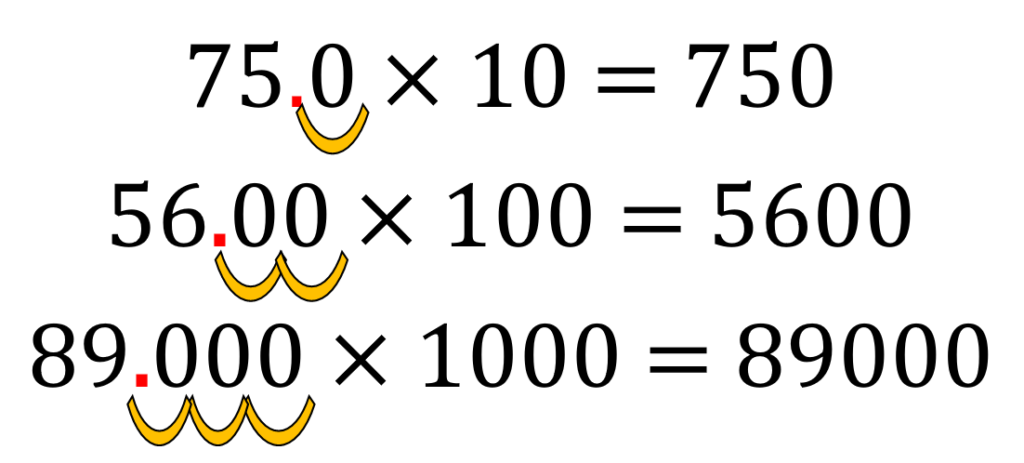
Examples ( Multiplying decimals by 10 )
- 45. 7 × 10 = 457
- 12. 65 × 10 = 126. 5
- 879.87 × 10 = 8798. 7
- 75030. 764 × 10 = 750307.64
- 1584.125 × 10 = 15841.25
Examples ( Multiplying decimals by 100 )
- 16.67 × 100 = 1667
- 32. 765 × 100 = 3276.5
- 8579.876 × 100 = 857987.6
- 71. 7654 ×100 = 7176.54
- 48.125 × 100 = 4812.5
Examples ( Multiplying decimals by 1000 )
- 25. 37 × 1000 = 25370
- 1213. 65 × 1000 = 1213650
- 87.7 × 1000= 87700
- 5600. 3 × 1000 = 5600300
- 198.1257 × 1000 = 198125.7
Word Problems
Example 1: Maria earns 10.25 dollars per hour for a job. If she worked 24 hours last month, how much did she earn?
Solution: To find her total earnings last month, we must multiply 10.25 by 24.
1 0 . 2 5
2 4
———–
4 1 0 0 (1025 × 4)
2 0 5 0 (1025 × 2)
————
2 4 6.0 0
Therefore, Maria earned 246 dollars last month in her job.
Example 2: John spends 12. 50 dollars per week for his dinner. How much would he spend on his dinner for 18 weeks?
Solution: To find how much will he spend for his dinner for 18 weeks, multiply 12.50 by 18.
1 2 . 5 0
1 8
———
1 0 0 0 0 (1250 × 8)
1 2 5 0 (1250 × 1)
———-
2 2 5.0 0
Thus, John would spend 225 dollars for 18 weeks for his dinner.
Example 3: A customer bought the following items below at a grocery store. Find how much did the customer pay.
3 pieces of cucumber for 0.71 dollars/piece
2.5 lbs. of apples for 2.25 dollars/lb.
1.9 lbs. of tomatoes for 2. 17 dollars/lb.
Solution:

Thus, 2.13 + 5.6250+4.123 = 11.878 dollars.
Example 4: Ashley recently joined an organization with a monthly membership of 18.87 dollars. If Ashley continues her membership for 7 months, how much will she spend?
Solution: To find how much will she spend for 7 months, multiply 18.87 by 7.
1 8 . 8 7
7
———–
1 3 2. 0 9
Thus, Ashley will spend a total of 132.09 dollars if she continues her membership for 7 months.
Example 5: It costs 5. 75 dollars per person to enter a museum. If there are 125 students to enter, how much would the total cost be?
Solution: To find how much would the total cost of 125 students entering the museum, multiply 5.75 by 125.
5 . 7 5
1 2 5
———-
2 8 7 5 ( 575 × 5 )
1 1 5 0 ( 575 × 2 )
5 7 5 ( 575 × 1 )
———————
71 8 .7 5
Therefore, the total cost is 718.75 dollars.
Summary
Steps in Multiplying with Decimals
Step 1: Arrange the given numbers such that one number is above the other number.
Step 2: Ignore the decimal points and multiply the numbers as whole numbers.
Step 3: Add the results together.
Step 4: Count the number of decimal places.
Step 5: Place a decimal point in the answer such that it has the same decimal places in the given numbers.
If we are multiplying decimals by 10, the decimal point moves 1 place to the right.
If we are multiplying decimals by 100, the decimal point moves 2 places to the right.
If we are multiplying decimals by 1000, the decimal point moves 3 places to the right.
Recommended Worksheets
Ordering Decimals (Holi Themed) Math Worksheets
Basic Operations of Decimals (Hanukkah Themed) Math Worksheets
Word Problems Involving Decimals (Market Themed) Math Worksheets









