Dilations | Definition, Examples, Kinds, Scaling, Center, Summary

Introduction

In geometry, transformations are available in different types: rotation, wherein we twist the orientation of a shape, translation, where we shift the position of a shape in the coordinate plane, and reflection, where we produce a flipped or mirrored version of a shape. We then introduce another kind of transformation that involves the scaling of a shape. This is what we call dilation.

What is Dilation?

Dilation is a transformation that resizes a geometrical shape while maintaining its orientation. We can think of dilation as enlarging or shrinking an object, like inflating a balloon, zooming in and out on a digital photo, or comparing two printouts of different sizes.

In this case, we can also say that dilation produces a similar shape as the original, since the proportion of the dimensions, as well as their angle measures, are preserved:

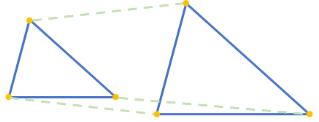
Kinds of Dilation

It is called enlargement when a dilation stretches a shape to become bigger. The lengths of the sides become larger in proportion to the original shape.

On the other hand, when a dilation shrinks a shape to become smaller, it is called reduction. The lengths of the sides become smaller in proportion to the original shape.

Scaling Factor

The relationship between the sizes of the original and scaled shapes can be quantified by what we call a scaling factor. The scaling factor is a ratio between the dimensions of the scaled shape and the original shape:

k=dimension of scaled shape÷dimension of original shape

We denote the scaling factor as a variable k, where we have a possible set of values:

If the absolute value of the scaling factor is greater than 1, we say that the original shape is an enlarged version of the original shape:

|k|>1

On the other hand, if the absolute value of the scaling factor is less than 1, we say that the scaled shape is a reduced version of the original shape:

|k|<1

Lastly, if the value of the scaling factor is exactly 1, we say that the scaled shape and the original shape are congruent:

k=1

Center of Dilation

An important concept in working with dilation in geometry is the reference at which we compare the sizes of shapes. The center of dilation is a fixed point in the coordinate plane where we can measure the distances of a shape’s vertices.

For example, we consider the quadrilateral □ABCD and the point X which will be our center of dilation:

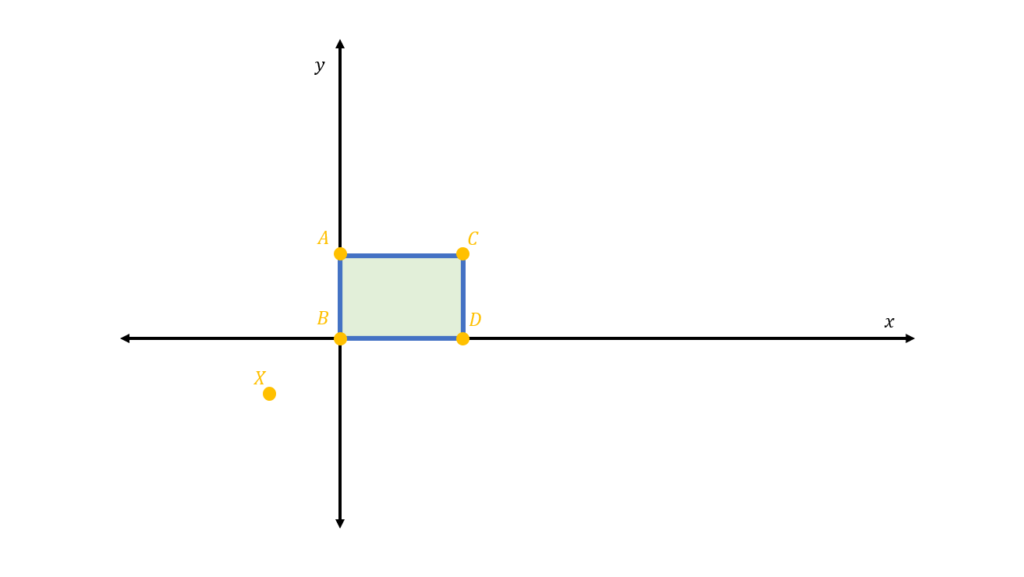
The distances between the vertices of the quadrilateral are given by their distance from the point X:

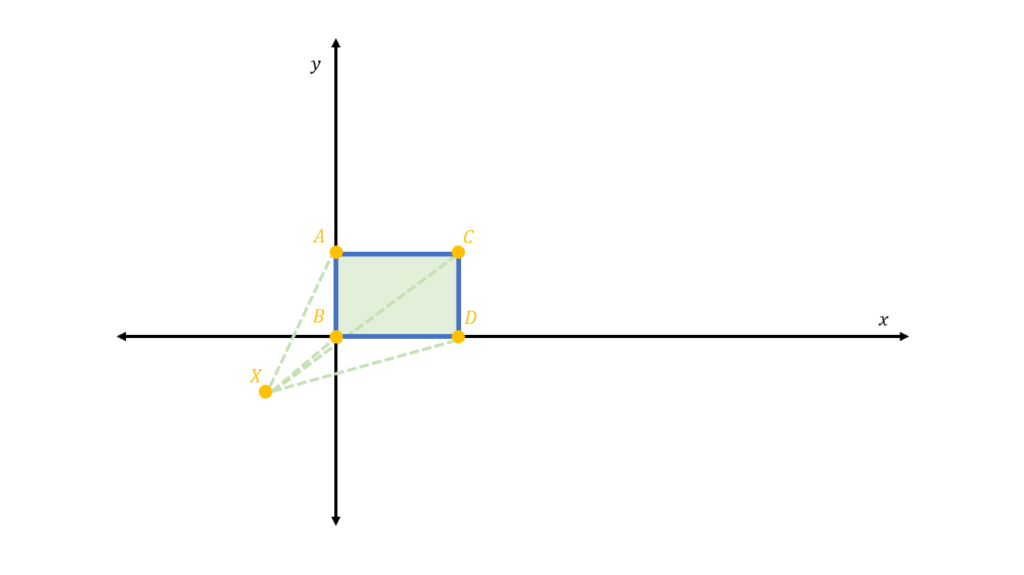
If we have a positive scaling factor that is greater than one, k>1, the scaled quadrilateral □A’B’C’D’ will have its vertices located at a farther distance from the center of dilation:

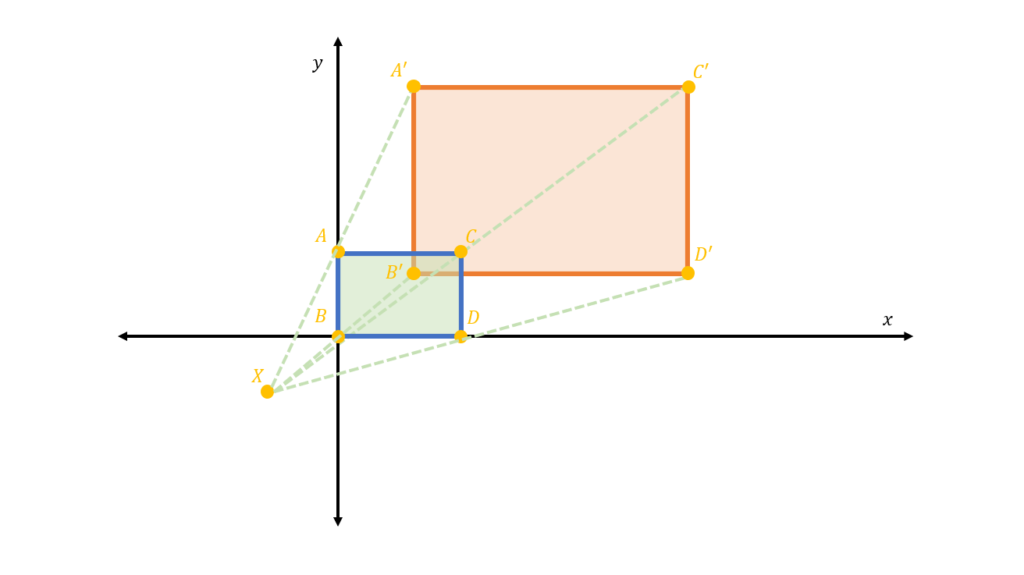
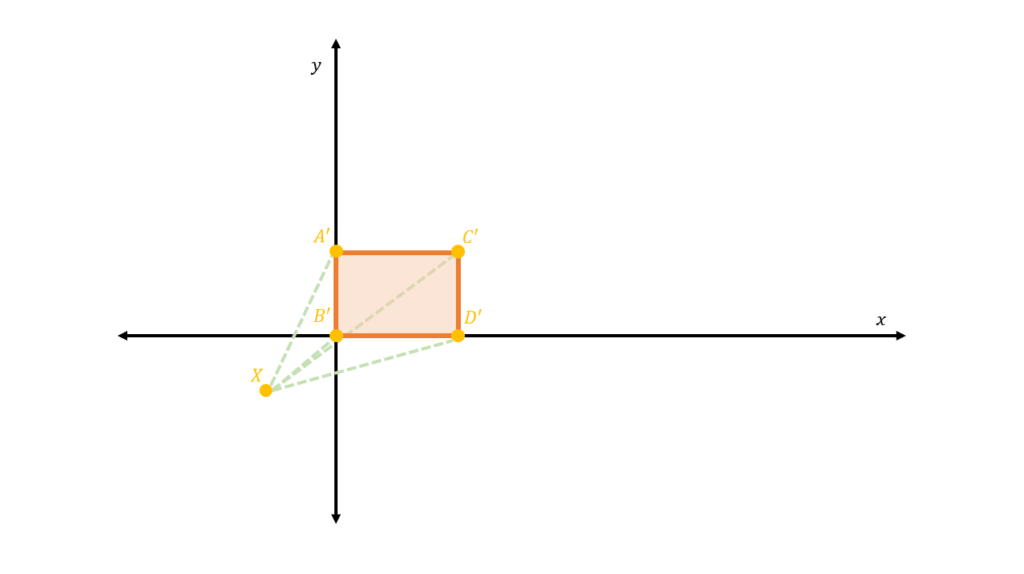
However, if we have a positive scaling factor that is less than one, k<1, the scaled quadrilateral □A’B’C’D’ will have its vertices located at a closer distance from the center of dilation:

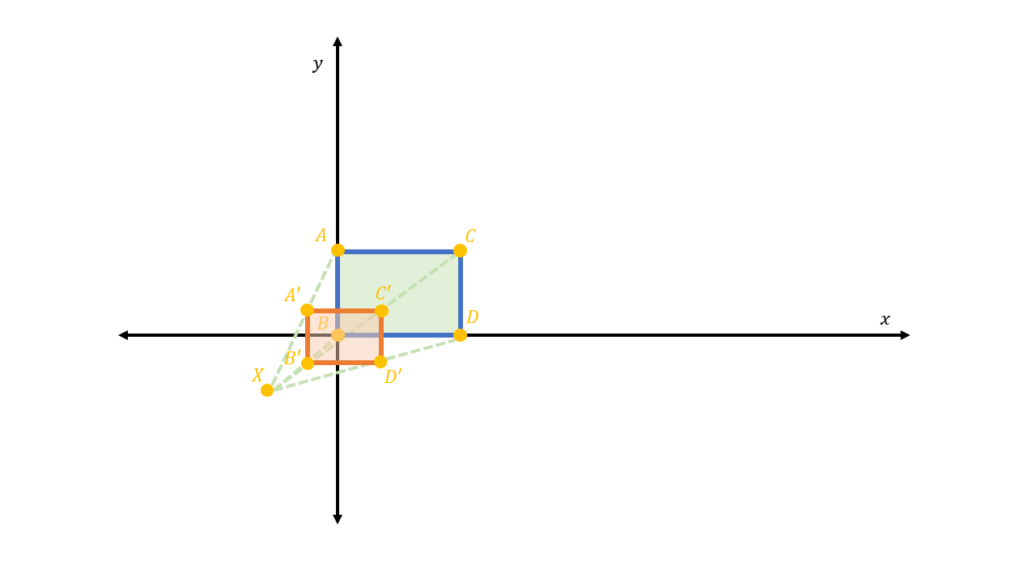
If we get a positive scaling factor that is equal to one, k=1, the scaled quadrilateral will be on top of the original quadrilateral as shown:

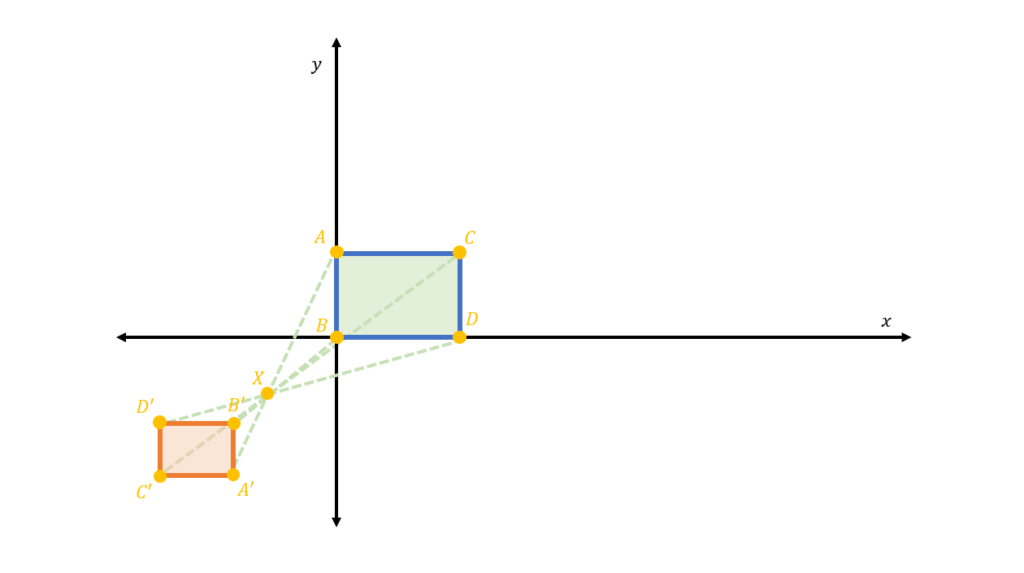
Lastly, we note that if we have a negative scaling factor the scaled quadrilateral □A’B’C’D’ will have an inverted orientation that is in an opposite direction from the center of dilation:

How to Perform Dilation

Now that we know about the process and types of dilation, we then discuss how we can perform dilations. For any given geometric figure in a coordinate plane, a dilation of scaling factor k can be done by scaling the coordinates of its vertices by the value of k:

A'(x,y) = A(kx,ky)

In the above equation, the coordinates of the scaled vertex A’ is obtained by multiplying both horizontal and vertical coordinates of the original vertex A by the scaling factor k.

We consider an example to guide us in learning how to perform dilation. In the figure below, we have a triangle ABC whose vertices are shown:

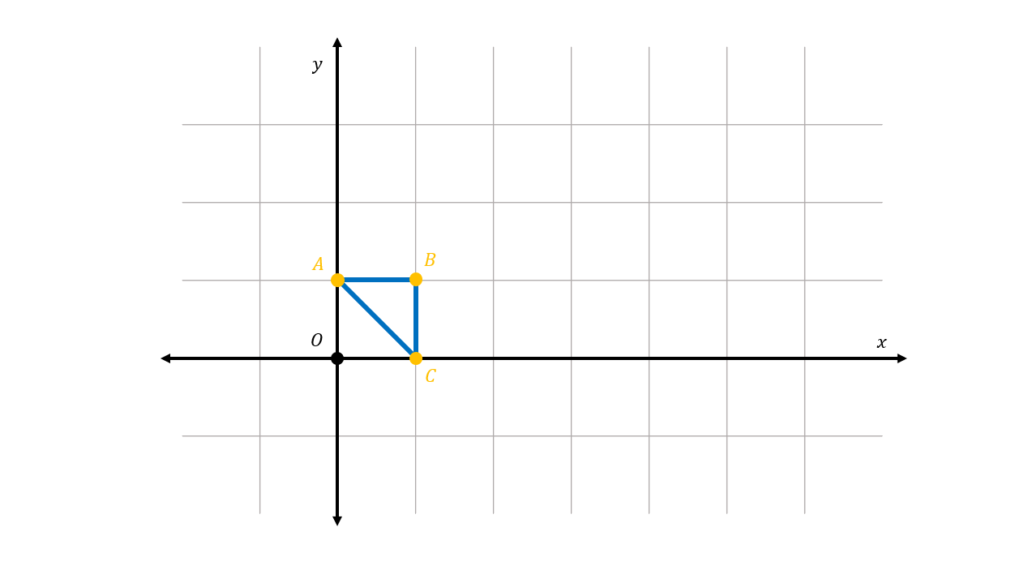
Suppose we have the center of dilation at the origin O(0,0), and the scaling factor is k=2. We wish to find the coordinates of the scaled triangle A’B’C’ using dilation.

We first find the coordinates of the scaled vertices A’, B’, and C’ by multiplying the scaling factor by the original coordinates:

A'(x,y) = A(kx,ky)

B'(x,y) = B(kx,ky)

C'(x,y) = C(kx,ky)

Substituting the given coordinates, we have:

A'(x,y) = A(2⋅0,2⋅1)

B'(x,y) = B(2⋅1,2⋅1)

C'(x,y) = C(2⋅1,2⋅0)

Hence, we have the coordinates of the scaled triangle △A’B’C’:

A'(0,2)

B'(2,2)

C'(2,0)

Plotting the points in the coordinate plane, we can see that the scaled triangle is twice the size of the original triangle:

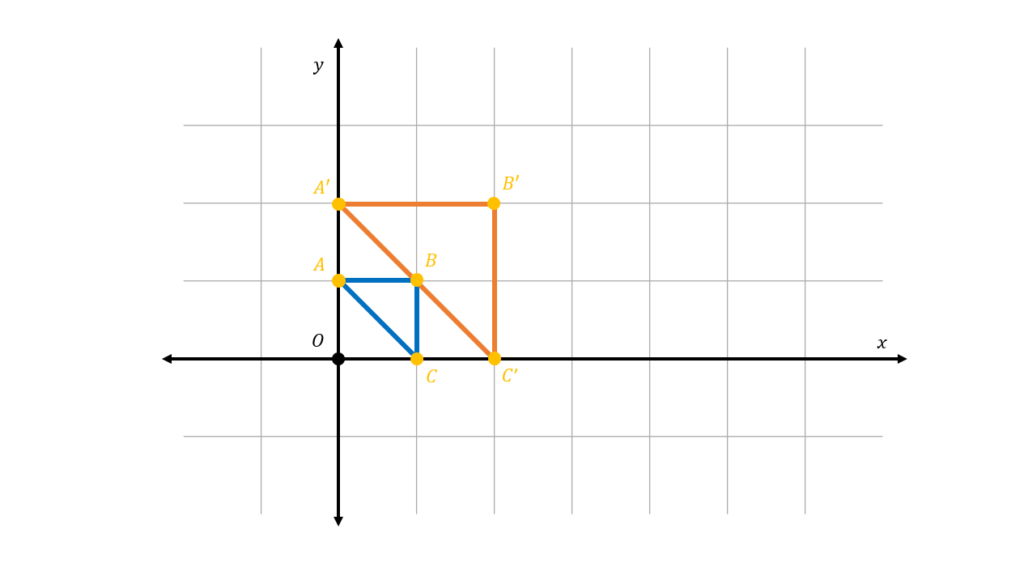
An alternative method we can use is through measuring the distances between the vertices and the center of dilation. If we take the distance between the vertices of the triangle and the origin, we have the lengths of the line segments formed by the center of dilation and each vertex as:

OA=1

OB= √2

OC=1

Then, we find the distance between the scaled vertices A’, B’, and C’ by multiplying the scaling factor k to the distances of the original vertices:

OA’=k⋅OA

OB’=k⋅OB

OC’=k⋅OC

Substituting the given distances, we have:

OA’ = 2⋅1 = 2

OB’ = 2⋅√2 = 2√2

OC’ = 2⋅1 = 2

We now plot the vertices of the scaled triangle △A’B’C’ by tracing the line formed by the original vertices and the center of dilation to the distances we have computed:

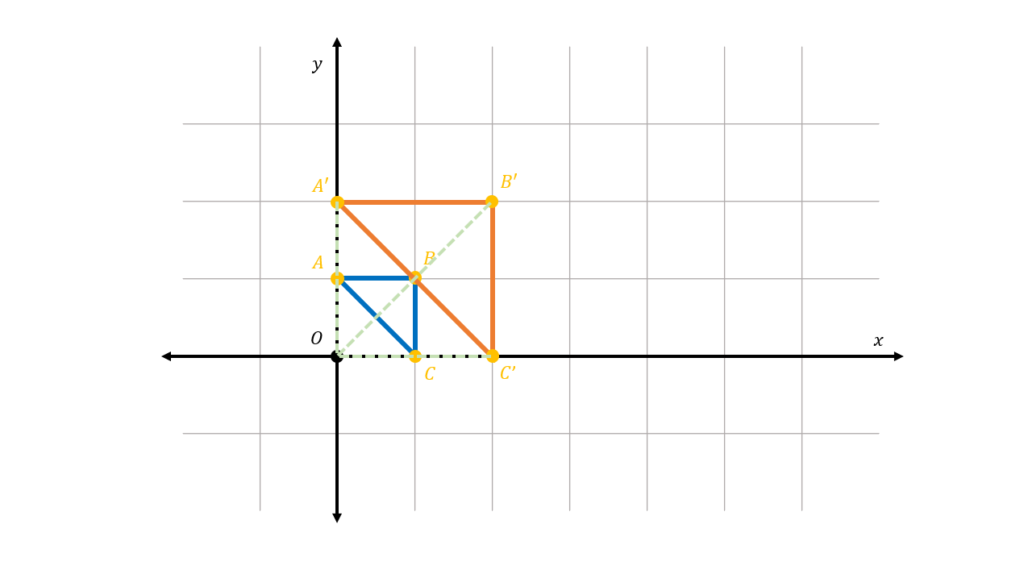
We can see that we have obtained the same result using either method.

Problem-Solving Examples

We can now proceed to solve sample problems to apply what we have learned so far. Each problem tackles different cases discussed and gives us a challenge on how to solve through the information given to us.

Sample Problem 1:

If we have a line segment $\overline{MN}$ that has its endpoints located at M(3,10) and N(5,7), what is the length of the scaled line segment $\overline{M’N’}$ if the scaling factor is 4?

Solution:

We are given the endpoints of the original line segment, and we know that the scaling factor is given by k=4. We can multiply the scaling factor to the coordinates of the endpoint M(3,10) to get its scaled coordinates:

M'(x,y) = M(kx,ky)

If we substitute the given scaling factor and the coordinates, we have:

M'(x,y) = M(4⋅3,4⋅10)

Then, we multiply both horizontal and vertical coordinates to get the coordinates of the scaled endpoint M’:

M(4⋅3,4⋅10) = M'(12,40)

Similarly, we repeat the same process for the other endpoint N(5,7). Multiplying the scaling factor to the coordinates of the original endpoint, we have:

N'(x,y) = N(kx,ky)

Substituting the given coordinates and the scaling factor, we can multiply them to obtain:

N'(x,y) = N(4⋅5,4⋅7)

∴N'(20,28)

Finally, we can solve for the length of the scaled line segment M’N’ using the distance formula:

M’N’ = $\sqrt{(x_N’-x_M’)^2 + (y_N’-y_M’)^2}$

Using the coordinates we have computed earlier, we can substitute them into the formula as follows:

M’N’=$\sqrt{(20-12)^2+(28-40)^2}$

Getting the difference between the horizontal and vertical coordinates, we get:

M’N’ = $\sqrt{(8)^2+(-12)^2}$

Then, squaring both numbers inside the radical we further simplify the expression into:

M’N’ = $\sqrt{64+144}$

Therefore, the length of the scaled line segment is given by √208 or 4√13:

M’N’ = √208 = 4√13

Now, since the problem only asks for the length of the line segment, we can use an alternative approach that makes use of the distance formula. Since dilation produces similar shapes, we know that the length of the scaled line segment $\overline{M’N’}$ is proportional to the length of the original line segment $\overline{MN}$ by the scaling factor k:

M’N’=k⋅MN

Using the distance formula, we can solve for the length of line segment $\overline{MN}$:

MN={$\sqrt{(5-3)^2+(7-10)^2}$

We take the difference between the horizontal and vertical coordinates inside the formula to get:

MN=$\sqrt{(2)^2+(-3)^2}$

Then, we square both results to further simplify the expression inside the radical:

MN = $\sqrt{4+9}=\sqrt{13}$

As such, we know the length of the original line segment to be MN=$\sqrt{13}$.

We can substitute this into the equation for getting the scaled length M’N’, along with the scaling factor k:

M’N’ = 4⋅$\sqrt{13}$

Therefore, we have shown through a more convenient method that the length of the scaled line segment is given by:

M’N’ = 4$\sqrt{13}$

Sample Problem 2:

Suppose we have an equilateral triangle △FGH shown in the figure below:

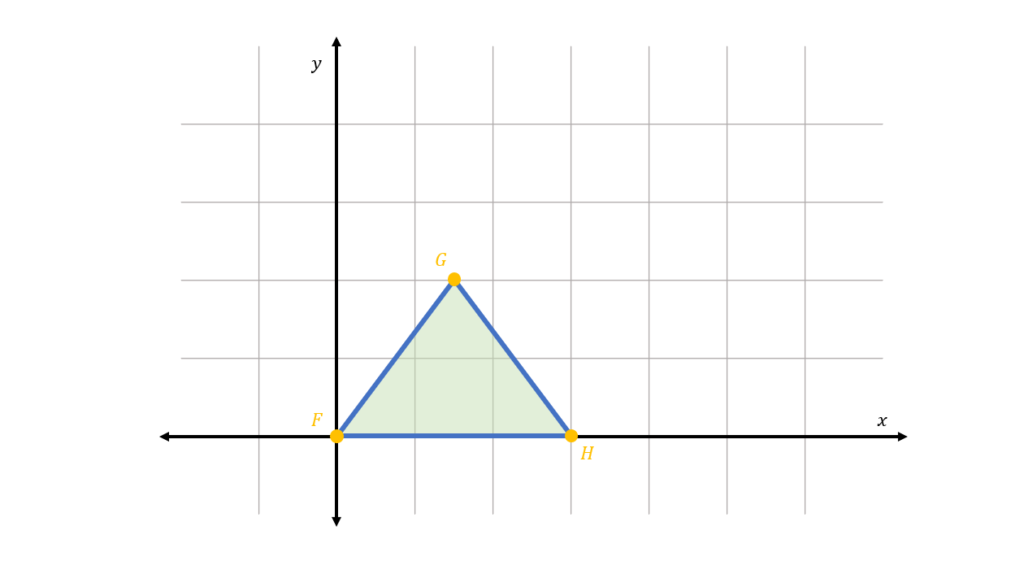
If we wish to scale it by twice its original size, what are the scaled coordinates of its vertices F’, G’, and H’?

Solution:

We first take note of the coordinates of the given triangle △FGH:

F(0,0)

G(1.5,2)

H(3,0)

Since we are scaling the triangle to twice its original size, we can say that the scaling factor is given by:

k=2

Then, we can determine the coordinates of the scaled triangle △F’G’H’ by multiplying the coordinates of the original triangle with the scaling factor:

F'(x,y) = F(kx,ky)

G'(x,y) = G(kx,ky)

H'(x,y) = H(kx,ky)

We first consider the vertex F. Substituting the given coordinates and the scaling factor, we have:

F'(x,y) = F(2⋅0,2⋅0)

Hence, the coordinates of the scaled vertex F’ can be obtained by evaluating the product of each coordinate:

F(2⋅0,2⋅0) = F'(0,0)

Next, we first consider the vertex G. Substituting the given coordinates and the scaling factor, we get:

G(x,y) = G(2⋅1.5,2⋅2)

Hence, the coordinates of the scaled vertex G’ can be computed by evaluating the product of each coordinate:

G(2⋅1.5,2⋅2) = G'(3,4)

Lastly, we first consider the vertex H. Substituting the given coordinates and the scaling factor, we have:

H'(x,y) = H(2⋅3,2⋅0)

Hence, the coordinates of the scaled vertex H’ can be obtained by evaluating the product of each coordinate:

H(2⋅3,2⋅0) = H'(6,0)

Therefore, the coordinates of the scaled triangle △F’G’H’ are:

F'(0,0)

G'(3,4)

H'(6,0)

Plotting the scaled triangle in the coordinate plane, we illustrate that it is indeed twice the size of the original triangle △FGH:

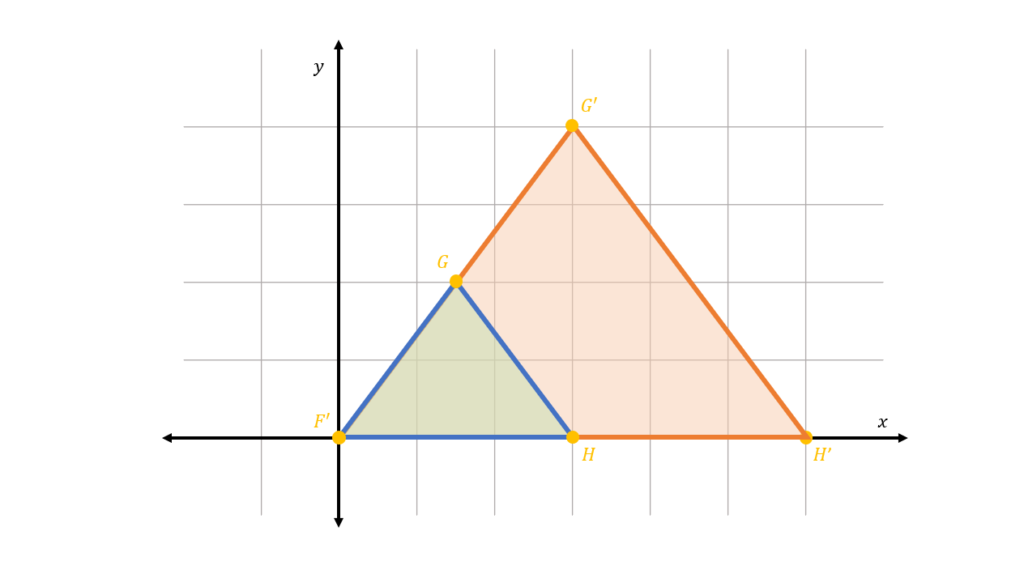
Sample Problem 3:

In the figure shown below, we have a circle of radius r=5 and whose center is located at C(0,10). If the center of dilation is located at a point X(-10,0), and the scaling factor is given by k=3, sketch the plot of the scaled circle.

Solution:

We first begin by illustrating the given. From the given radius and center of the circle, we can plot the shape as well as the center of dilation as shown:

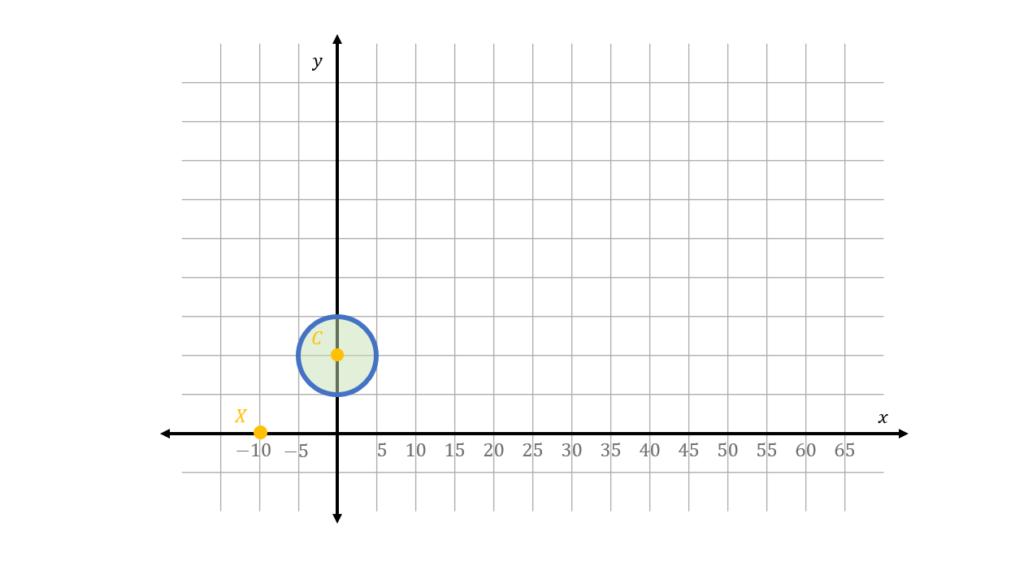
Then, we measure the distance between the center of dilation X and the center of the circle C. By the distance formula, we have:

XC=$\sqrt{(0+10)^2 + (10-0)^2}$

Evaluating the radical expression, we obtain the distance XC:

XC=$\sqrt{(10)^2 + (10)^2}$

∴XC = 2√10

Next, we determine the distance between the center of dilation X and the center of the scaled circle C’. We do this by multiplying the length XC by the scaling factor k:

XC’=k⋅XC

Substituting the computed distance XC, we obtain the value of the unknown length XC’:

XC’=3⋅2√10 = 6√10

Hence, we can trace the line formed by segment XC by length XC’ to get the coordinates of the center C’. Visually, we extend the distance by thrice the length of XC:

Finally, we note that the radius of the scaled circle is proportional to the radius of the original circle by the scaling factor. Hence, we know that the radius of the scaled circle is thrice the radius of the original circle:

r’=k⋅r

Substituting the given radius and scaling factor, we solve for the radius of the scaled circle:

r’=3⋅5=15

Therefore, we can plot points along the scaled circle following the computed radius r’:

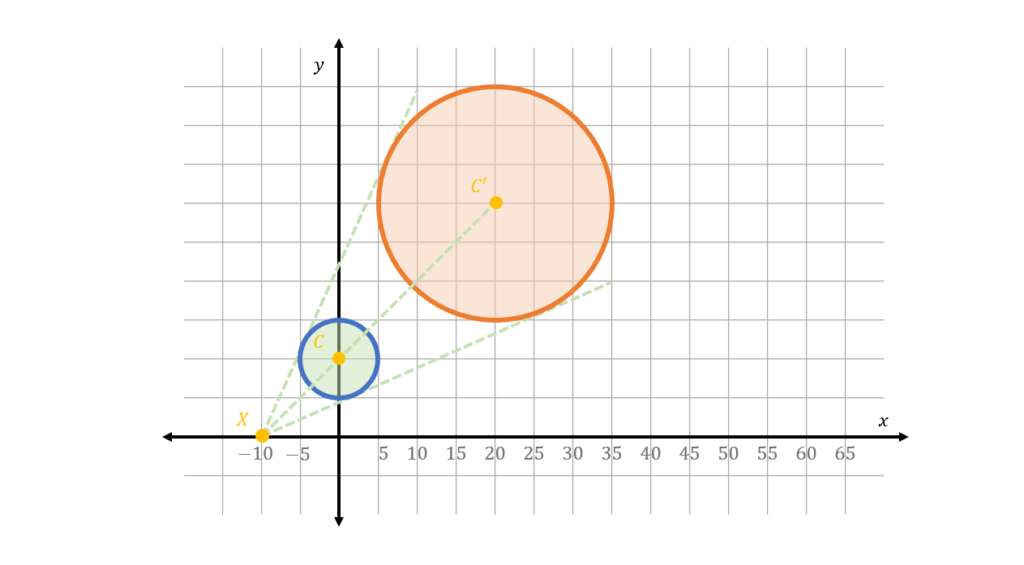
Summary

Dilation is a transformation that resizes a geometrical shape while maintaining its orientation. This transformation results in similar shapes.

It is called enlargement when a dilation stretches a shape to become bigger. The lengths of the sides become larger in proportion to the original shape.

On the other hand, when a dilation shrinks a shape to become smaller, it is called reduction. The lengths of the sides become smaller in proportion to the original shape.

The scaling factor is a ratio between the dimensions of the scaled shape and the original shape:

k=dimension of scaled shape÷dimension of original shape

If the absolute value of the scaling factor is greater than 1, we say that the original shape is an enlarged version of the original shape:

|k|>1

On the other hand, if the absolute value of the scaling factor is less than 1, we say that the scaled shape is a reduced version of the original shape:

|k|<1

Lastly, if the value of the scaling factor is exactly 1, we say that the scaled shape and the original shape are congruent:

k=1

The center of dilation is a fixed point in the coordinate plane where we can measure the distances of a shape’s vertices.

For any given geometric figure in a coordinate plane, a dilation of scaling factor k can be done by scaling the coordinates of its vertices by the value of k:

A'(x,y) = A(kx,ky)

Frequently Asked Questions (FAQs)

How do we know that two shapes are similar?

For two shapes to be similar, we have the following conditions:

The lengths of its corresponding sides/edges are proportional to each other
The angle measures of its corresponding interior angles are equal

For example, two triangles △ABC and △XYZ are said to be similar if the following conditions hold:

The lengths of their sides are proportional to each other

$\frac{AB}{XY} = \frac{AC}{XZ} = \frac{BC}{YZ}$

The measures of their corresponding angles are equal

∠A≅∠X

∠B≅∠Y

∠C≅∠Z

How do we find the coordinates of a point?

If the coordinates of a point are not given, and its plot on the coordinate plane is shown instead, we can look at the horizontal and vertical distance the point has from the origin:

Suppose we have the point A and we want to know its coordinates (x,y). To do this, we first measure how many steps the point is from the x-axis:

From the origin (0,0), we measure three steps to the positive direction of the x-axis. Hence, we say that the x-coordinate of point A is 3:

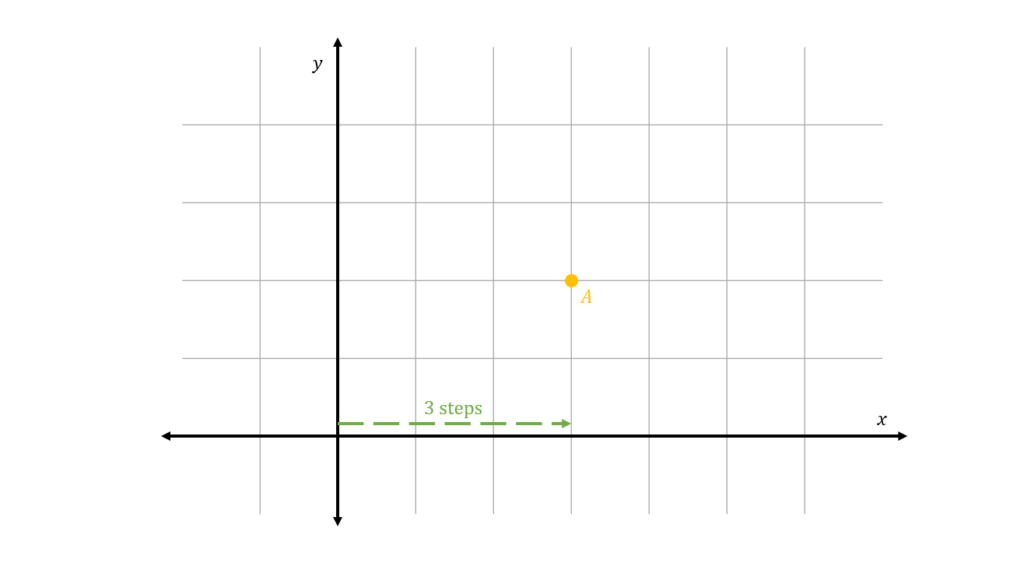
Next, we then measure how many steps the point is from the y-axis:

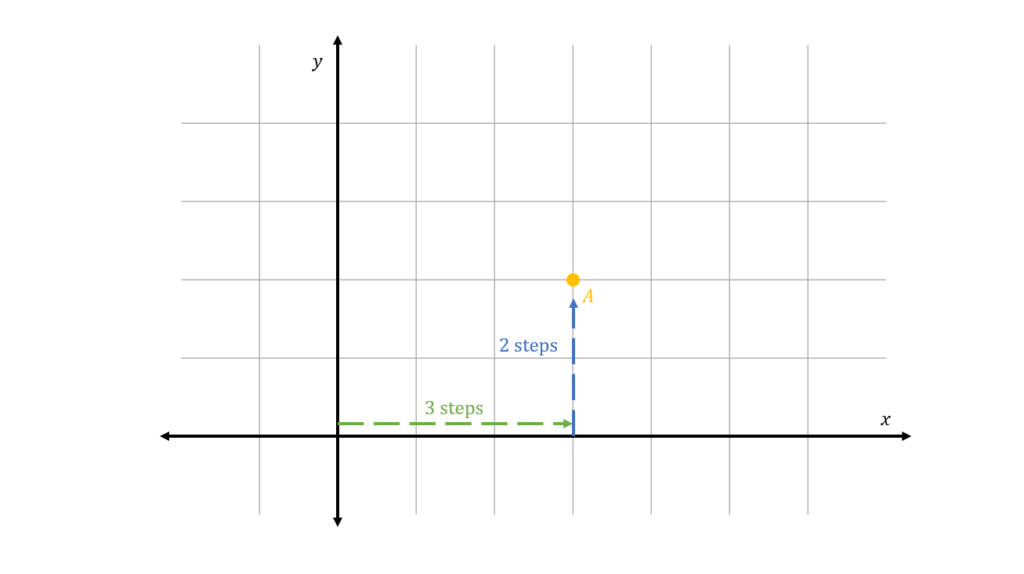
From the point (3,0), we measure two steps to the positive direction of the y-axis. Hence, we say that the y-coordinate of point A is 2.

Therefore, we conclude that the coordinates of point A is given by:

A(3,2)

How do we measure the distance between two points?

To measure the distance between two points, we make use of the distance formula:

d = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Here, d denotes the distance between points (x₁,y₁) and (x₂,y₂).

How do we use the distance formula?

We first need two points whose coordinates are known. Then, we substitute these x and y coordinates to the formula. We can use designate either point as the first point or the second point, as long as the substitution remains consistent in the formula.

After evaluating the expression inside the radical, we can then obtain the distance between those said points.

Recommended Worksheets

Distance Formula of Two Points 6th Grade Math Worksheets
Cartesian Coordinate Plane (Adventure Themed) Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!