Introduction
Trigonometry has applications in both mathematics and physics. Applications of trigonometry include calculating height, distances, angles of elevation, and angles of depression.
Let’s say, for instance, that an observer on the roof of a building is looking at a car on the road; from the observer’s point of view, there is an angle of depression generated toward the car. Using trigonometric ratios like sine, cosine, and tangent, the angle of depression helps in the computation of distances.
The angle of depression associated terminologies and calculation process will all be covered in this article.
Angle of Depression
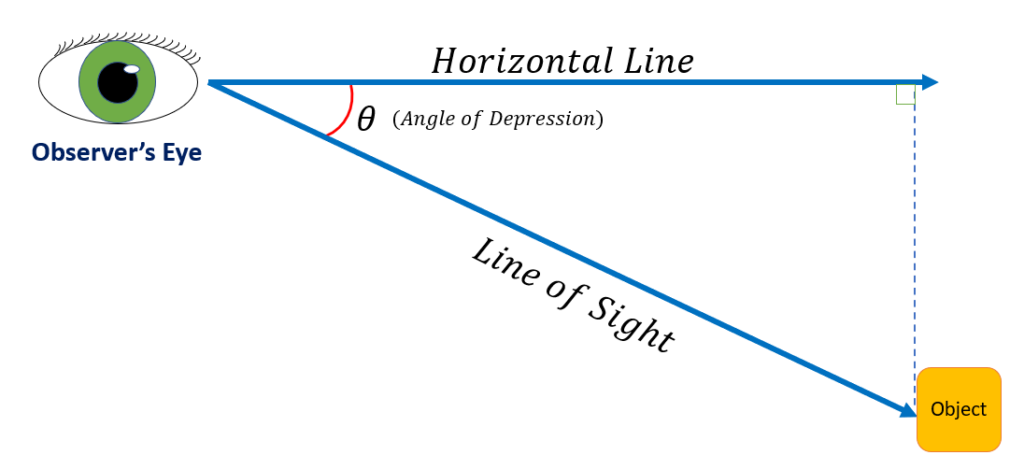
The angle of depression is formed by the line drawn between an object below the observer’s eye and a horizontal line or plane. The line that the observer’s eye is on is called the line of sight. The angle of depression is therefore constructed such that, as the name implies, it is below the observer’s eye.
For instance, as seen in the figure below, an observer focuses on an object. The angle of depression is represented by θ.
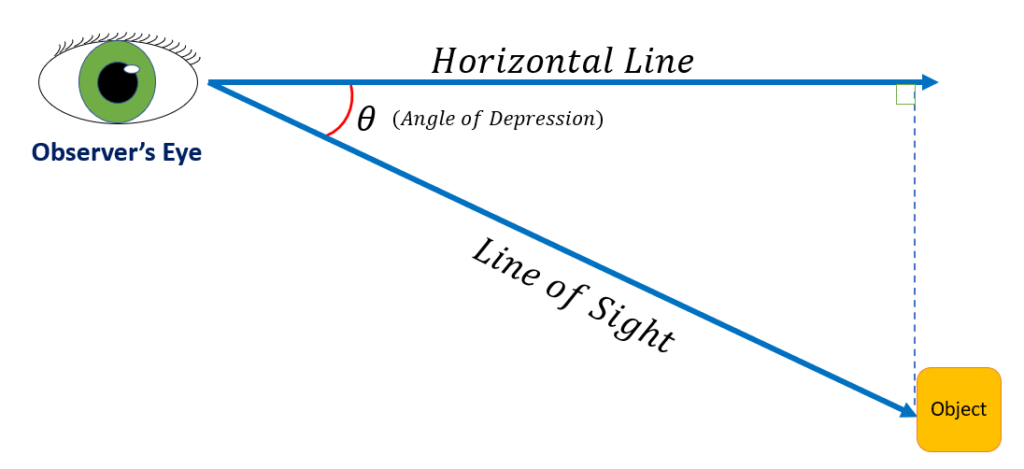
If we join the horizontal line and the object vertically, in this case, we get a right-angle triangle. So, we can calculate the observer’s distance from the object using trigonometry. The height of the object will be viewed as the opposite side of θ of the constructed triangle, and the horizontal line will be considered the adjacent side of the triangle.
Keywords Associated with Angle of Depression
These are the terms we must be familiar with when dealing with the angle of depression.
Angle
When two straight rays or lines meet at a single point, an angle is created. Degrees are used to express angles.
Line of Sight
The line of sight is the line drawn from the observer’s eye to the object being viewed. It is an oblique line which is therefore not horizontal nor vertical. The line of sight, together with the horizontal line, forms the angle of depression.
Horizontal Line
The horizontal line is a straight line on a flat surface. In a coordinate system, a horizontal line has points with the same y-coordinate. The line of sight, together with the horizontal line, forms the angle of depression.
Observer’s Eye
The observer’s eye is the position where the line of sight and the horizontal line meet.
The Angle of Depression vs. Angle of Elevation
The opposite of an elevation angle is the angle of depression. The object is placed at an angle of elevation above the observer, as opposed to being placed at an angle of depression below the observer. If you are standing and staring at something on a rooftop, you will generate an angle of elevation. However, if you look at the plants on the ground, an angle of depression is created. The heights and distances in both scenarios can be determined using trigonometric concepts.
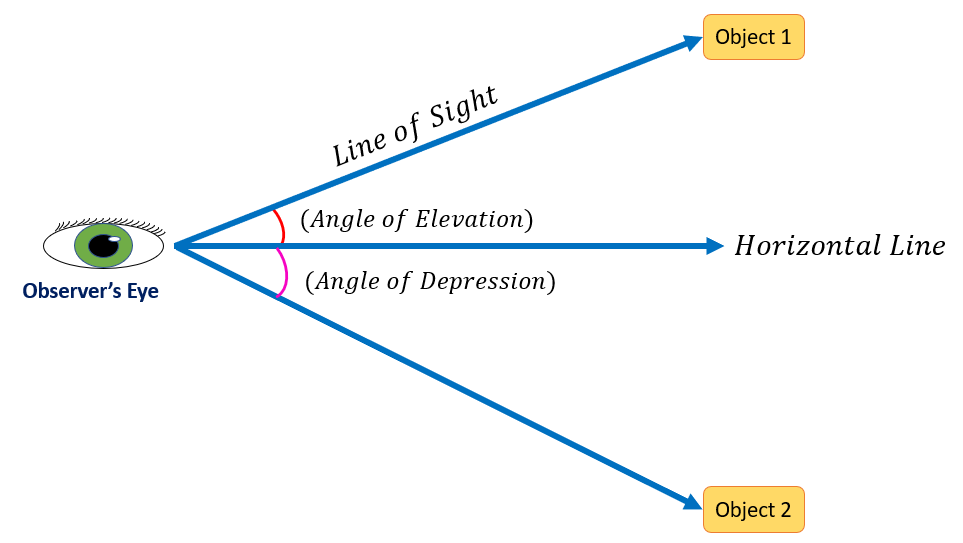
The table below shows the difference between the angle of elevation and depression.
| Angle of Depression | Angle of Elevation |
| When an object is positioned below the observer’s eye level, an angle of depression is formed. | When an object is positioned above the observer’s eye level, the angle of elevation is formed. |
| Regarding the angle of depression, the horizontal line is above the object. | Regarding the angle of elevation, the horizontal line is below the object. |
The Angle of Depression Formulas
Some formulas are used to calculate the angle of depression.
Let’s use the illustration below to demonstrate how we apply the formulas. Recall that a right-angle triangle will be constructed if an imaginary vertical line is drawn between the object to the end of the horizontal line. Therefore, we may use the idea of trigonometry to calculate how far the observer is from the object. The position of the object will be viewed as the opposite side of θ, and the horizontal line will be considered the adjacent side of the created triangle.
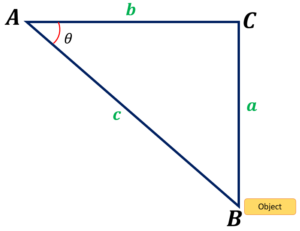
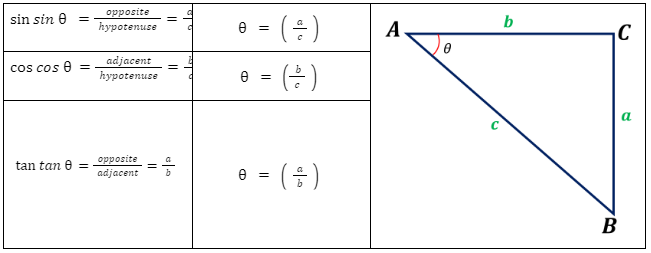
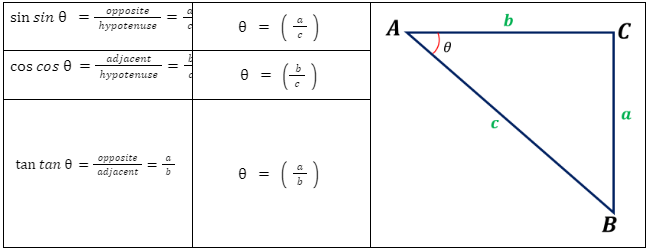
In the figure, side a is the opposite side of , side b is the adjacent side, and side c is the hypotenuse or length of the line of sight.
To determine the angle of depression, we can use the formulas below, provided we know the angles’ two sides.
| sin sinθ =$\frac{opposite}{hypotenuse}$=$\frac{a}{c}$ | θ = ($\frac{a}{c}$) |
| cos cosθ=$\frac{adjacent}{hypotenuse}$=$\frac{b}{c}$ | θ = ($\frac{b}{c}$) |
| tan tanθ=$\frac{opposite}{adjacent}$=$\frac{a}{b}$ | θ = ($\frac{a}{b}$) |
If we must calculate the angle of depression given the line of sight and the vertical distance of the object from the horizontal line, we can use the sine formula θ = ($\frac{a}{c}$).
If we must calculate the angle of depression given the hypotenuse or the line of sight and the adjacent side of , we can use the cosine formula θ = ($\frac{b}{c}$).
If we must calculate the angle of depression given the opposite side of and the adjacent side of , we can use the tangent formula θ = ($\frac{a}{b}$).
For example, in the figure below, we must calculate the length of segment BC.

In the given triangle ABC, ∠A is the angle of depression, side AC is the adjacent side, and side BC is the opposite of the angle θ. Since we know two sides of the triangle, opposite and the adjacent sides of the angle , we must use the formula for the tangent.
AC ( adjacent side ) = 50 meters
BC ( opposite side ) = 29 meters
Thus, we have,
tan tanθ=$\frac{opposite\: side}{adjacent\: side}$
tan tanθ=$\frac{29\: meters}{50\: meters}$
tan tanθ=0.58
Therefore, θ=( 0.58 )
Hence, the value of θ ≈ 30°.
Examples
Example 1
Find the value of the angle of depression ( θ ) in each of the given figures.
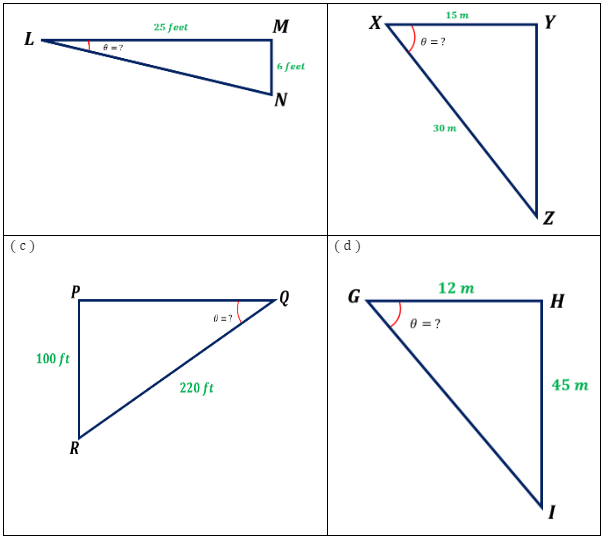
Solution
( a ) In the given triangle LMN, ∠L is the angle of depression, side MN is the opposite side, and side LM is the adjacent side of the angle θ. Since we know two sides of the triangle, opposite and the adjacent sides of the angle , we must use the formula for the tangent.
MN (opposite side ) = 6 ft
LM ( adjacent side ) = 25 ft
Thus, we have,
tan tanθ=$\frac{opposite\: side}{adjacent\: side}$
tan tanθ=$\frac{6\: ft}{25\: ft}$
tan tanθ=0.24
Therefore, θ=( 0.24 )
Hence, the value of θ ≈ 13.50°.
( b ) In the given triangle XYZ, ∠Y is the angle of depression, side XZ is the length of the line of sight or the hypotenuse of the triangle, while side XY is the adjacent side of the angle θ. Since we know the lengths of the hypotenuse and the adjacent side of the angle , we must use the formula for cosine.
XZ ( hypotenuse side ) = 30 m
XY ( adjacent side ) = 15 m
Thus, we have,
cos cosθ=$\frac{adjacent\: side}{hypotenuse\: side}$
cos cosθ=$\frac{15\: m}{30\: m}$
cos cosθ=0.50
Therefore, θ=( 0.50 )
Hence, the value of θ = 60°.
( c ) In the given triangle PQR, ∠Q is the angle of depression, side QR is the length of the line of sight or the hypotenuse of the triangle, while side PR is the opposite side of the angle θ. Since we know two sides of the triangle, hypotenuse and the opposite side of the angle , we must use the formula for sine.
QR (hypotenuse side ) = 220 ft
PR ( opposite side ) = 100 ft
Thus, we have,
sin sinθ=$\frac{opposite\: side}{hypotenuse\: side}$
sin sinθ=$\frac{100\: ft}{220\: ft}$
sin sinθ=0.45
Therefore, θ=( 0.45 )
Hence, the value of θ ≈ 27°.
( d ) In the given triangle GHI, ∠H is the angle of depression, side HI is the opposite side of , while side GH is the adjacent side of the angle θ. Since we know two sides of the triangle, the adjacent and the opposite side of the angle , we must use the formula for the tangent.
HI ( opposite side ) = 45 m
GH ( adjacent side ) = 12 m
Thus, we have,
tan tanθ=$\frac{opposite\: side}{adjacent\: side}$
tan tanθ=$\frac{45\: m}{12\: m}$
tan tanθ≈3.75
Therefore, θ=( 3.75 )
Hence, the value of θ ≈ 75°.
Example 2
When looking down from a tower’s top, the angle of depression of a car is at a 30-degree angle. Determine the tower’s height if the car is 150 meters from the building.
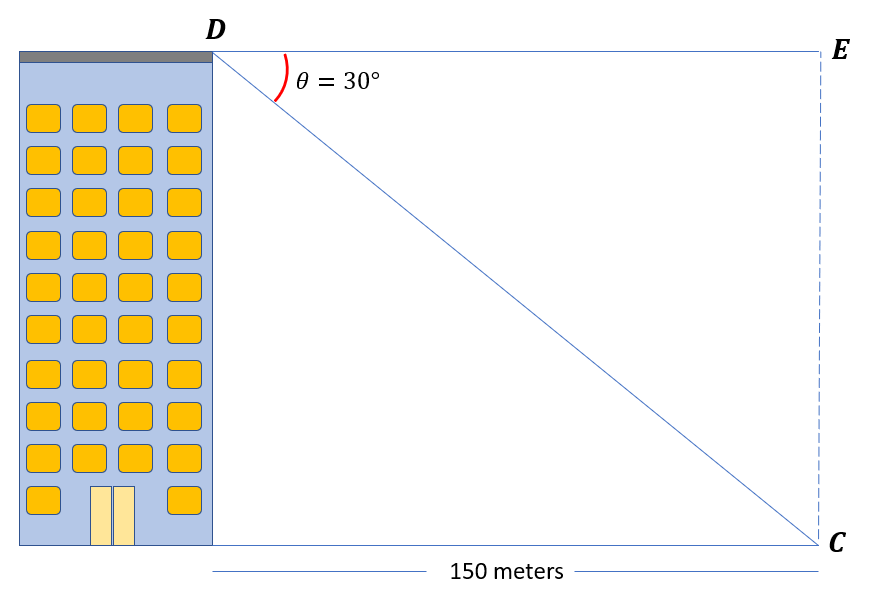
Solution
In the figure above, ∠D is the angle of depression that measures 30°, and C is the car. The car’s distance from the tower is the same as the length of the line segment DE. The line segment QC is the line of sight, while line segment CE is the tower’s height.
The opposite side of angle θ is the height of the tower. Let us use the formula for tangent since the problem involves the triangle’s opposite and adjacent sides. Thus, we have,
tan tanθ=$\frac{opposite\: side}{adjacent\: side}$
tan tan30°=$\frac{height\: of\: the\: tower}{150\: m}$
tan tan30° ( 150 m ) = height of the tower
86.60 m ≈ height of the tower
height of the tower ≈ 86.60 m
Hence, the height of the tower is approximately 86.60 m.
Example 3
From a cliff, the angle of depression of a boat is °50. Find the boat’s horizontal distance from the cliff if the line of sight or hypotenuse is 75 feet long, as indicated in the image below.
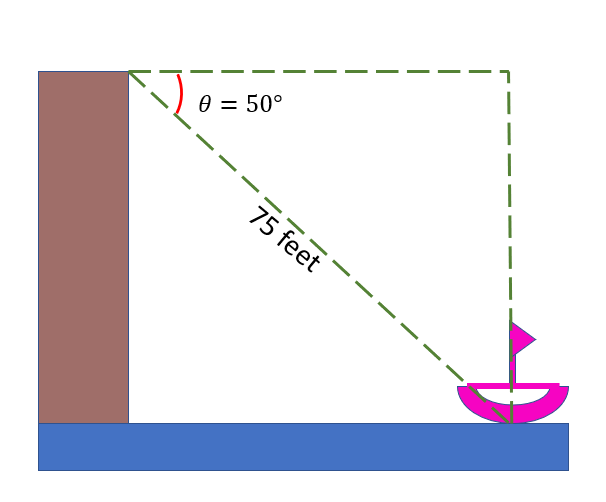
Solution
Let us label the vertices of the triangle formed in the given figure.
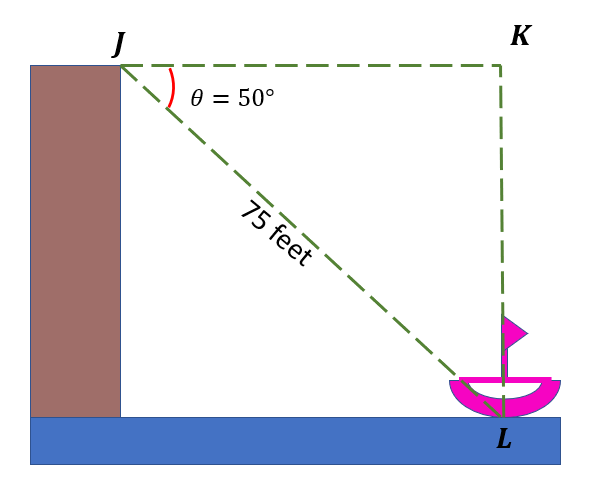
Here, we have ∠J as the angle of depression, and the line segment JL measures 75 feet. Since we must calculate the horizontal distance of the boat from the cliff, it is getting the length of the line segment JK.
We will use the cosine formula since we know and the hypotenuse of the triangle. Hence we have,
JL ( hypotenuse side ) = 75 feet
θ=50°
Thus, we have,
cos cosθ=$\frac{adjacent\: side}{hypotenuse\: side}$
cos cos50°=$\frac{adjacent\: side}{75\: feet}$
cos cos50° ( 75 feet ) = adjacent side
48.21 ≈ adjacent side
Hence, the distance of the boat from the cliff is 48.21 feet.
Summary
Angle of Depression
The angle of depression is formed by the line drawn between an object below the observer’s eye and a horizontal line or plane. The line that the observer’s eye is on is called the line of sight. The angle of depression is therefore constructed such that, as the name implies, it is below the observer’s eye.
Keywords Associated with Angle of Depression
| Angle When two straight rays or lines meet at a single point, an angle is created. Degrees are used to express angles. | Observer’s Eye The observer’s eye is the position where the line of sight and the horizontal line meet. |
| Horizontal Line The horizontal line is a straight line on a flat surface. In a coordinate system, a horizontal line has points with the same y-coordinate. The line of sight, together with the horizontal line, forms the angle of depression. | Line of Sight The line of sight is the line drawn from the observer’s eye to the object being viewed. It is an oblique line which is therefore not horizontal nor vertical. The line of sight, together with the horizontal line, forms the angle of depression. |
The Angle of Depression vs. Angle of Elevation
The table below shows the difference between the angle of elevation and depression.
| Angle of Depression | Angle of Elevation |
| When an object is positioned below the observer’s eye level, an angle of depression is formed. | When an object is positioned above the observer’s eye level, the angle of elevation is formed. |
| Regarding the angle of depression, the horizontal line is above the object. | Regarding the angle of elevation, the horizontal line is below the object. |
The Angle of Depression Formulas
To determine the angle of depression, we can use the formulas below, provided we know the angles’ two sides.
If we must calculate the angle of depression given the line of sight and the vertical distance of the object from the horizontal line, we can use the sine formula θ = ( $\frac{a}{c}$ ).
If we must calculate the angle of depression given the hypotenuse or the line of sight and the adjacent side of , we can use the cosine formula θ = ( $\frac{b}{c}$ ).
If we must calculate the angle of depression given the opposite side of and the adjacent side of , we can use the tangent formula θ = ( $\frac{a}{b}$ ).
Frequently Asked Questions on Angle of Depression ( FAQs )
What is meant by the angle of depression?
The angle of depression is formed by the line drawn between an object below the observer’s eye and a horizontal line or plane. The line that the observer’s eye is on is called the line of sight. The angle of depression is therefore constructed such that, as the name implies, it is below the observer’s eye.
What are the terms associated with the angle of depression?
Angle, line of sight, horizontal line, and the observer’s eye are the terms we must be familiar with when dealing with the angle of depression.
Angle
When two straight rays or lines meet at a single point, an angle is created. Degrees are used to express angles.
Line of Sight
The line of sight is the line drawn from the observer’s eye to the object being viewed. It is an oblique line which is therefore not horizontal nor vertical. The line of sight, together with the horizontal line, forms the angle of depression.
Horizontal Line
The horizontal line is a straight line on a flat surface. In a coordinate system, a horizontal line has points with the same y-coordinate. The line of sight, together with the horizontal line, forms the angle of depression.
Observer’s Eye
The observer’s eye is the position where the line of sight and the horizontal line meet.
What distinguishes the angle of elevation from the angle of depression?
The opposite of an elevation angle is the angle of depression. The object is placed at an angle of elevation above the observer, as opposed to being placed at an angle of depression below the observer. If you are standing and staring at something on a rooftop, you will generate an angle of elevation. However, if you look at the plants on the ground, an angle of depression is created. The heights and distances in both scenarios can be determined using trigonometric concepts.
The table below shows the difference between the angle of elevation and depression.
| Angle of Depression | Angle of Elevation |
| When an object is positioned below the observer’s eye level, an angle of depression is formed. | When an object is positioned above the observer’s eye level, the angle of elevation is formed. |
| Regarding the angle of depression, the horizontal line is above the object. | Regarding the angle of elevation, the horizontal line is below the object. |
How do we calculate the angle of depression?
To determine the angle of depression, we can use the formulas below, provided we know the angles’ two sides.
| sin sinθ =$\frac{opposite}{hypotenuse}$=$\frac{a}{c}$ | θ = ($\frac{a}{c}$) |
| cos cosθ=$\frac{adjacent}{hypotenuse}$=$\frac{b}{c}$ | θ = ($\frac{b}{c}$) |
| tan tanθ=$\frac{opposite}{adjacent}$=$\frac{a}{b}$ | θ = ($\frac{a}{b}$) |
If we must calculate the angle of depression given the line of sight and the vertical distance of the object from the horizontal line, we can use the sine formula θ = ($\frac{a}{c}$).
If we must calculate the angle of depression given the hypotenuse or the line of sight and the adjacent side of , we can use the cosine formula θ = ($\frac{b}{c}$).
If we must calculate the angle of depression given the opposite side of and the adjacent side of , we can use the tangent formula θ = ($\frac{a}{b}$).
For example, in the figure below, we must calculate the length of segment BC.
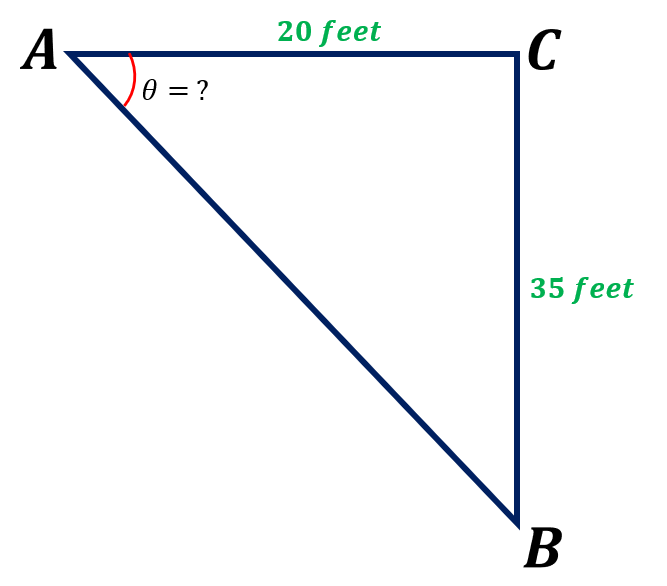
In the given triangle ABC, ∠A is the angle of depression, side AC is the adjacent side, and side BC is the opposite of the angle θ. Since we know two sides of the triangle, opposite and the adjacent sides of the angle , we must use the formula for the tangent.
AC ( adjacent side ) = 20 feet
BC ( opposite side ) = 35 feet
Thus, we have,
tan tanθ=$\frac{opposite\: side}{adjacent\: side}$
tan tanθ=$\frac{35\: feet}{20\: feet}$
tan tanθ=1.75
Therefore, θ=( 1.75 )
Hence, the value of θ ≈ 60.26°.
In a right triangle, how do you calculate distance using the angle of depression?
As an illustration, let us use the triangle below with vertices ZBC and θ as the given angle of depression.
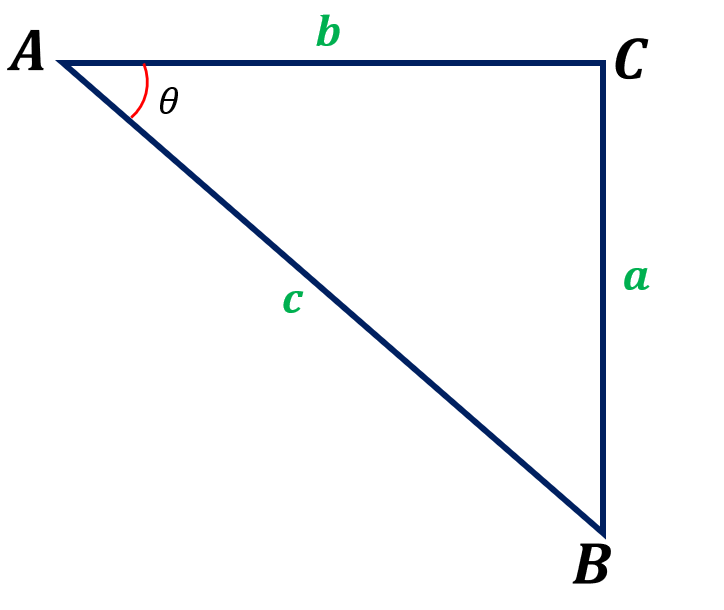
Let us say we want to calculate the distance or length of each side, a, b, and c.
To calculate side a, we will use the cosine formula which involves the adjacent side b and the hypotenuse side c. Hence we have,
cos cosθ=$\frac{adjacent\: side}{hypotenuse}$
cos cosθ=$\frac{b}{c}$
θ) c =b
Adjacent side of = ( cos θ ) ( c )
Therefore, the adjacent side is the product of the hypotenuse and cosine θ.
To calculate side b, we will use the sine formula which involves the opposite side a and the hypotenuse side c. Hence we have,
sin sinθ=$\frac{opposite\: side}{hypotenuse}$
sin sinθ=$\frac{a}{c}$
( sin θ ) ( c ) = a
The opposite side of = ( sin θ ) ( c )
Therefore, the opposite side of θ is the product of the hypotenuse and sine θ.
To calculate side c, we will use the sine or the cosine formula. Hence, we have,
| cos cosθ=$\frac{adjacent\: side}{hypotenuse}$ cos θ=$\frac{b}{c}$ c=$\frac{b}{coscos\:θ}$ Hypotenuse = $\frac{b}{coscos\:θ}$ Therefore, the hypotenuse is the adjacent side divided by the value of cosine θ. | sin sinθ=$\frac{opposite\: side}{hypotenuse}$ sin θ=$\frac{a}{c}$ c = $\frac{a}{sinsinθ}$ Hypotenuse = $\frac{b}{sinsinθ}$ Therefore, the hypotenuse is the opposite side divided by the value of sin θ. |
What is the importance of the angle of depression and angle of elevation?
Mathematical and physical uses of trigonometry exist. Calculating height, distance, angles of elevation, and angles of depression are all applications of trigonometry. As a result, it is crucial to learn and comprehend the angle of elevation and depression as they are both used in several applications that entail measurements, especially when precision is crucial.
Recommended Worksheets
Spatial Skills: Angles (Human Rights Day Themed) Math Worksheets
Horizontal and Vertical Line (Women’s History Month Themed) Math Worksheets
Parallel and Perpendicular Lines (Songkran Festival Themed) Math Worksheets









