Introduction
Before we cover more about the inscribed angle theorem and proving, let us first recall some essential definitions of inscribed angles and related concepts.
We must remember the difference between a central angle and an inscribed angle. An angle is inscribed if its sides are the chords of the circle and its vertex is on the circle. The radii of the same circle serve as the sides of a central angle, which has its vertex at the circle’s center. The image below shows an inscribed angle and a central angle.
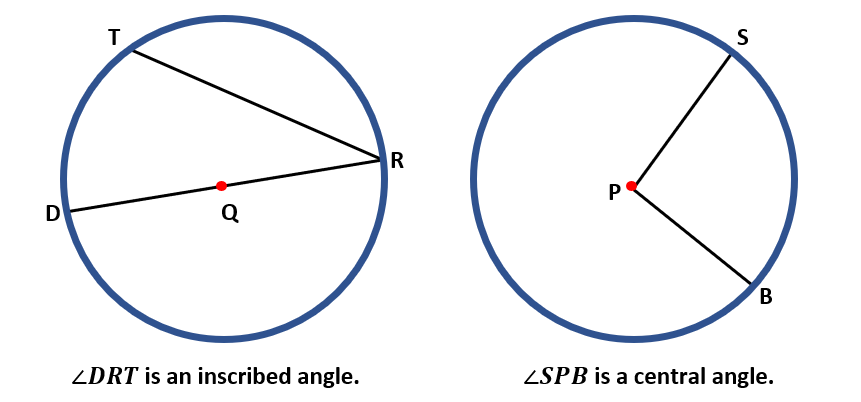
∠DRT is an inscribed angle since its two sides, $\overline{DR}$ and $\overline{RT}$, are chords of circle Q, and its vertex, point R, is on the circle. ∠SPB is a central angle since its sides are the radii $\overline{PB}$ and $\overline{PS}$ and its vertex, point P, is the center of the circle.
Another term that must also be clear is the intercepted arc. The intercepted arc is the part of the circle between the intersection points of the sides of the angle and the circle. In the previous example, arc DT is the intercepted arc of the inscribed angle ∠DRT while arc SB is the intercepted arc of the central angle ∠SPB.
Learning the difference between the inscribed and central angles is crucial in proving theorems to apply previous knowledge regarding equation manipulation and properties easily.
Inscribed Angle Theorem
Definition
According to the inscribed angle theorem, the central angle’s measure is equal to double that of the inscribed angle.
Let us try to examine the illustration below,
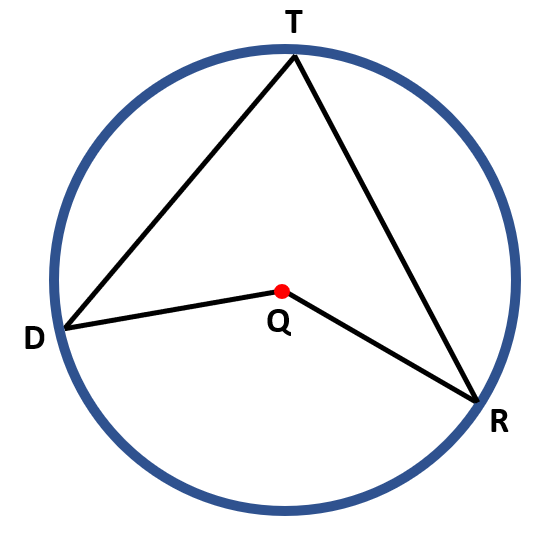
∠DQR is a central angle.
∠DTR is an inscribed angle.
By the inscribed angle theorem,
∠DTR=½ ∠DQR or
∠DQR=2 (∠DTR)
Let us have the following examples and identify the measurement of the missing angle.
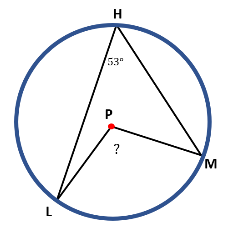 | ∠LHM is an inscribed angle, while ∠LPM is a central angle. To find ∠LPM, ∠LPM=2 ( ∠LHM ) ∠LPM = 2( 53° ) ∠LPM=106° |
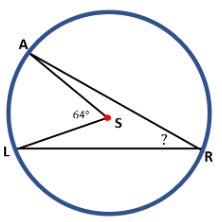 | ∠LRA is an inscribed angle, while ∠LSA is a central angle. To find ∠LRA, ∠LRA=½ ( ∠LSA ) ∠LRA=½ ( 64° ) ∠LRA=$\frac{64°}{2}$ ∠LRA=32° |
Proof of Inscribed Angle Theorem
Three distinct cases must be considered when proving the Inscribed Angle Theorem. These three cases cover every scenario based on the diameter’s location and the inscribed angle in the given circle.
The three cases are:
Case 1: When the diameter is one of the chords forming the inscribed angle.
Case 2: When the diameter is in the interior of the inscribed angle
Case 3: When the diameter is in the exterior of the inscribed angle.
Case 1: When the diameter is one of the chords forming the inscribed angle.
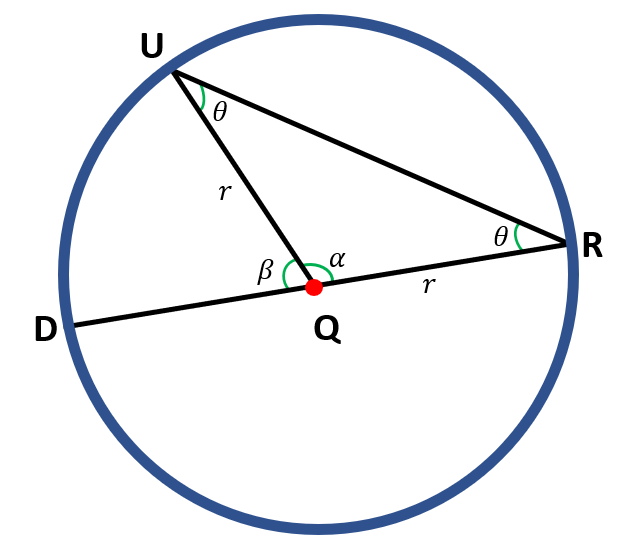
Here, we can see that the diameter of circle Q is one of the chords forming the inscribed angle ∠DRU. We will prove that the measure of the central angle β is twice that of the inscribed angle θ.
In this case, $\overline{QU}$ and $\overline{QR}$ are both radii of circle Q; thus, they have the same length, r. The points Q, U, and R form a triangle. Since the two sides have the same length, $\overline{QU}$ and $\overline{QR}$, then ∆QUR is isosceles. Since we know that isosceles triangles have congruent base angles, we have,
∠QUR ≅ QRU = θ
Angle is an exterior angle to ∆QUR. Hence, by the exterior angle theorem, β is equal to the sum of angles ∠QUR and ∠QRU
| β+α=180° | Straight angle measure 180° |
| α+θ+θ=180° | Sum of the interior angles |
| β+α=α+θ+θ | Transitive property of equality |
| β=θ+θ | Subtraction property of equality subtracted from both sides of the equation |
| β=2θ | Addition property |
Hence, we have proven that for this case, where the diameter of circle Q is one of the chords forming the inscribed angle ∠DRU, the measure of the central angle is twice the measure of the inscribed angle θ.
Case 2: When the diameter is in the interior of the inscribed angle
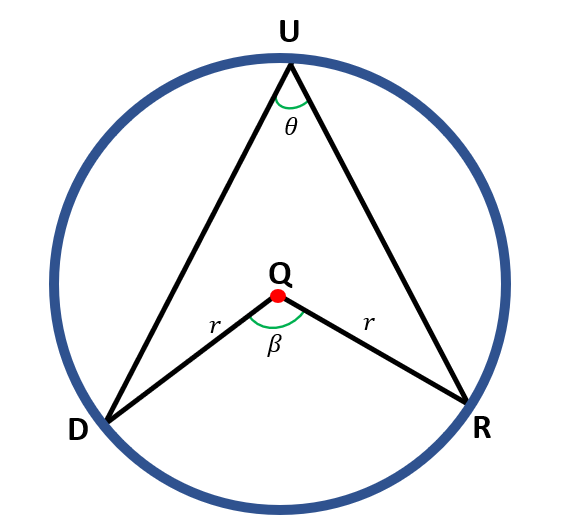
Here, we can see that circle Q has a central angle ∠DQR and an inscribed angle ∠DUR. Also, the two radii, $\overline{QD}$ and $\overline{QR}$, are given.
Using the first case we have just proved, let us draw a diameter of the circle that bisects the angles ∠DUR ( θ ) and ∠DQR ( β ).
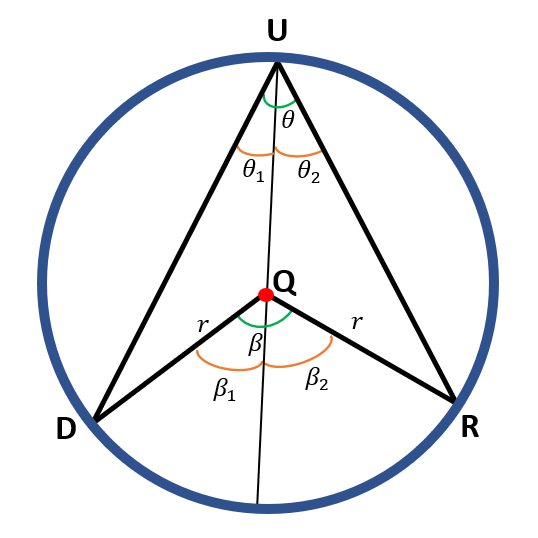
Thus, we have,
θ=θ1+θ2
β=β1+β2
Using the first case above, we already know that,
β1=2θ1
β2=2θ2
If we add the equations we have,
| β1+β2 = 2θ1 + 2θ2 | Transitive property of equality |
| β1+β2 = 2 ( θ1+ θ2 ) | Factoring |
| β=2θ | Substitution, β=β1+β2 and θ=θ1+ θ2 |
Hence, we have proven that the measure of the central angle is twice that of the inscribed angle θ.
Case 3: When the diameter is in the exterior of the inscribed angle.
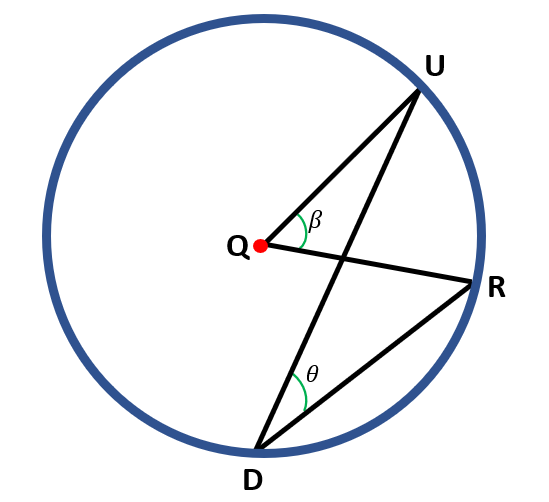
In this figure, we can say that the inscribed angle is ∠UDR ( θ ), and the central angle is ∠UQR ( β ).
To prove that m ∠ UQR=2 (m ∠ UDR ), let us first draw the diameter of the circle outside the inscribed angle.
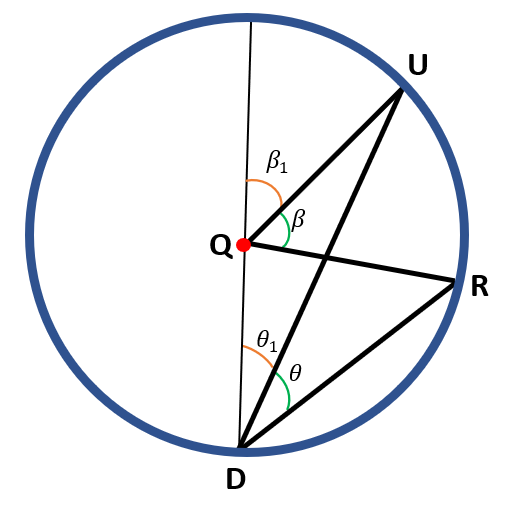
In the figure above, we can have the following information,
θ, θ1 and θ+θ1 are all inscribed angles and
β1 is a central angle that subtends the same arc as θ1,
β+β1 is a central angle that subtends the same arc as θ+θ1.
Using the proven case above, when the diameter is one of the chords forming the inscribed angle, we can have the following equations:
( 1 ) β1 = 2θ1
( 2 ) β1+β = 2( θ + θ1 )
Substituting equation (1 ) to equation ( 2 ),
2θ1 + β = 2( θ + θ1)
2θ1 + β = 2θ + 2θ1.
Subtract 2θ1 to both sides of the equation,
2θ1 – 2θ1 + β = 2θ + 2θ1 – 2θ1
β=2θ
Thus, we have proven that the measure of the central angle is double that of the inscribed angle θ.
More Examples
Example 1
In each case below, determine the value of x.
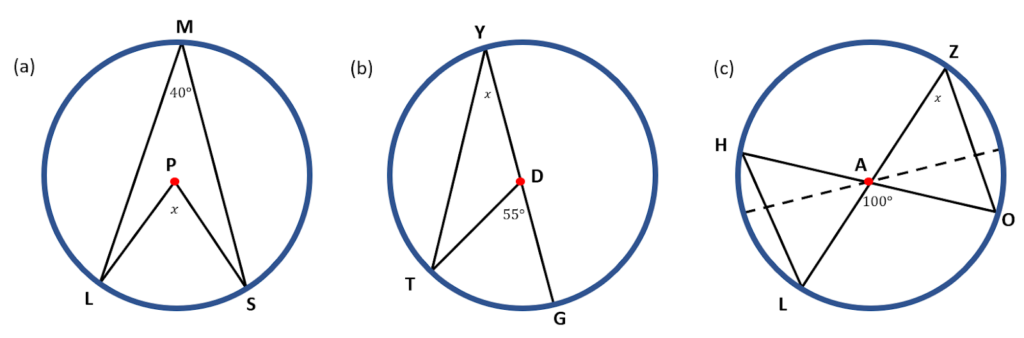
Solution:
( a ) The inscribed angle is ∠LMS, while the central angle is ∠LPS. Notice that these angles have the same intercepted arc LS. Since we are asked to get the value of x, which is the measure of the central angle (∠LPS), we must multiply the measurement of the inscribed angle (∠LMS) by 2. Hence,
∠LPS=2 (∠ LMS)
∠LPS=2( 40° )
∠LPS = 80°
Thus, ∠LPS measures 80 degrees.
( b ) The inscribed angle is ∠TYG. The central angle is ∠TDG. These angles have the same intercepted arc TG. Since the missing angle is the inscribed angle, we must get ½ of the measure of the central angle (∠TDG). Thus, we have,
∠TYG=½( ∠ TDG)
∠TYG = ½( 55°)
∠TYG = 27.5°
Hence, ∠TYG measures 27.5 degrees.
( c ) The central angle ∠LAO and the inscribed angle ∠LZO have the same intercepted arc LO. Therefore, to get the value of x, which is the inscribed angle ( ∠LZO), we must get ½ of the measure of the central angle ∠LAO.
∠LZO=½( ∠ LAO)
∠LZO = ½( 100°)
∠LZO=50°
Therefore, ∠LZO measures 50 degrees.
Example 2
Find the value of x and y where ∠CGE=40° and ∠FGD=45°.
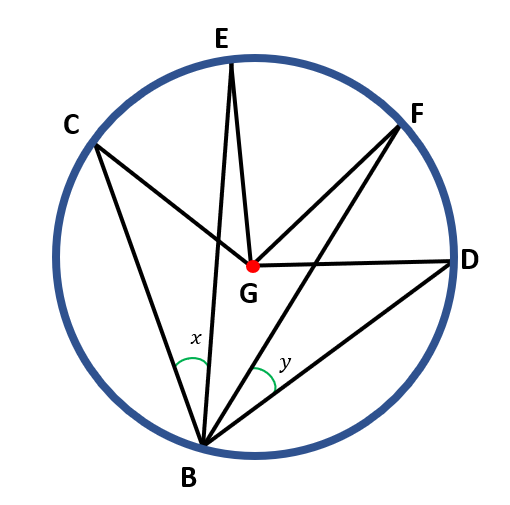
Solution:
In the given figure, the missing angles x and y are both inscribed angles since their vertices are on the circle and their sides are chords of the circle. Both angles ∠CGE and ∠FGD, are central angles. ∠CGE and x have the same intercepted arc, while ∠FGD and y have the same intercepted arc. Therefore, to find the values of x and y, by the inscribed angle theorem, we must get ½ of the measure of the central angles ∠CGE and ∠FGD, respectively.
For the value of x,
x = ½ ( ∠ CGE )
x = ½ ( 40° )
x = $\frac{40°}{2}$
x = 20°
For the value of y,
y = ½ ( ∠ FGD )
y = ½ ( 45° )
y = $\frac{45°}{2}$
y = 22.5°
Therefore, the value of x is 20 degrees while the value of y is 22.5 degrees.
Example 3
Determine the value of x and y if ∠LVP=46° and ∠PMN=48
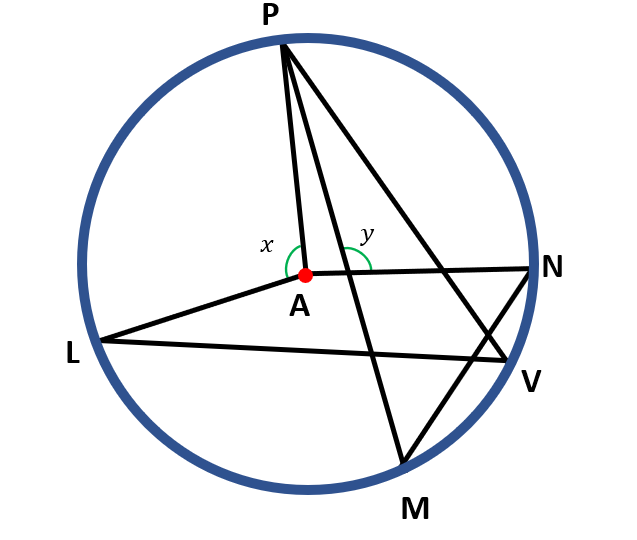
Solution:
From the figure, the angles ∠LVP and ∠PMN are both inscribed angles. We are looking for the value of x and y, which are both central angles. Notice that ∠LVP has the same intercepted arc with x. Also, ∠PMN has the same intercepted arc with y. By inscribed angle theorem, we must double the measurement of the inscribed angles ∠LVP and ∠PMN to get the value of x and y, respectively. Hence, we have,
For the value of x,
x = 2 ( ∠ LVP )
x = 2 ( 46° )
x = 92°
For the value of y,
y = 2 ( ∠ PMN )
y = 2 ( 48° )
y = 96°
Therefore, x=92° while y=96°.
Example 4
Find the value of x.

Solution:
In the given circle with center K, ∠GTR is an inscribed angle that measures 110°. To get the measure of the central angle ∠GKR, we must multiply the m ∠ GTR by 2. Remember that the measure of a central angle is twice the measure of the inscribed angle if they share the same intercepted arc. Hence,
m ∠ GKR=2 ( m ∠ GTR )
m ∠ GKR=2 ( 110° )
m ∠ GKR = 220°
Let us now equate (4x+60)° to 220° to find the value of x. We have,
4x + 60 = 220
4x = 220 – 60
4x = 160
$\frac{4x}{4}$ = $\frac{160}{4}$
x = 40
Therefore, the value of x is 40.
Example 5
In the illustration below, suppose that ∠TGY = (7x+5)° and ∠TDY=80°, find the value of x.
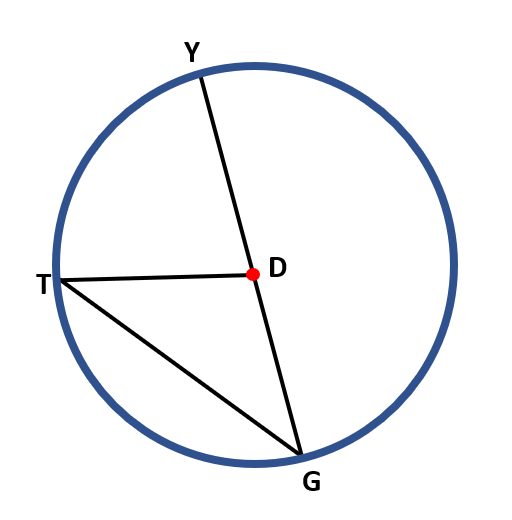
Solution:
In the given illustration, ∠TDY is a central angle, while ∠TGY is an inscribed angle. These angles have the same intercepted arc. Hence, by the inscribed angle theorem, the measure of the inscribed angle (∠TGY) is ½ the measure of the central angle (∠TDY). So, we have,
∠TGY = ½ (∠TDY)
∠TGY = ½ ( 80° )
∠TGY = $\frac{80°}{2}$
∠TGY = 40°
Now let us find the value of x since we already know that ∠TGY is equal to 40°. Thus,
7x + 5 = 40
7x = 40 – 5
7x = 35
$\frac{7x}{7}$ = $\frac{35}{7}$
7x = 5
Therefore, the value of x is 5.
Example 6
In the figure below, ∠PON measures 150°. Find the measure of ∠PIN.
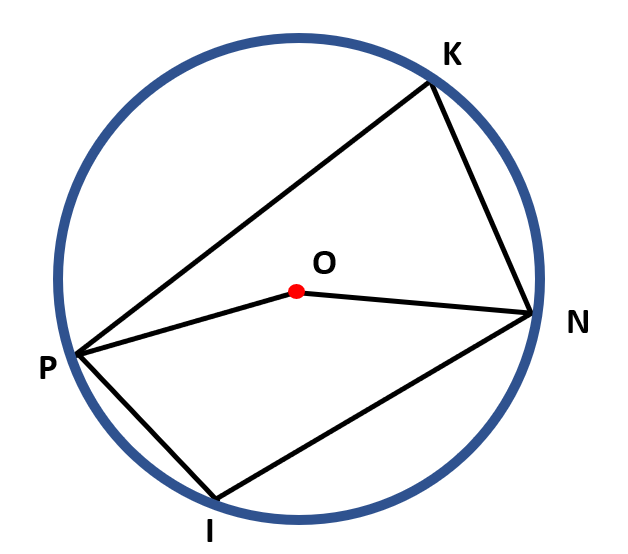
Solution:
∠PON is a central angle in the given figure, while ∠PIN is an inscribed angle. It can also be observed that the points P, I, N, and K form an inscribed quadrilateral.
Since the inscribed angle, ∠PON, and central angle ∠PKN has the same intercepted arc, the measure of ∠PKN is half the measure of ∠PON. That is,
∠PKN = ½ ( ∠PON )
∠PKN = ½ (150°)
∠PKN = $\frac{150°}{2}$
∠PKN = 75°
Since we already know that ∠PKN measures 75°, we may get the measure of the ∠PIN. Remember that the total measurement of the opposite angles of a quadrilateral inscribed in a circle is 180°. It means that the angles ∠PKN and ∠PIN are supplementary. Hence,
∠PKN +∠PIN = 180°
∠PIN = 180° – ∠PKN
∠PIN = 180° – 75°
∠PIN = 105°
Therefore, ∠PIN measures 105 degrees.
Example 7
Find the value of x, ∠N, and ∠K if ∠LFT=120°.
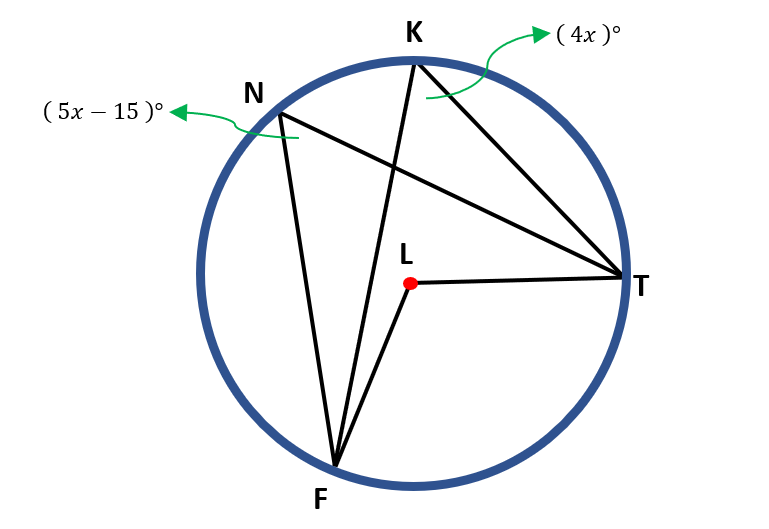
Solution:
From the given figure, ∠LFT is a central angle while ∠N and ∠K are both inscribed angles. It can also be observed that ∠LFT, ∠N, and ∠K have the same intercepted arc. Therefore, to get the measure of both angles ∠N and ∠K, we must get ½ of the measure of ∠LFT. So, we have,
∠N= ½ ( ∠LFT )
∠N = ½( 120° )
∠N = $\frac{120°}{2}$
∠N=60°
Since ∠K and ∠N have the same intercepted arc, their angle measures are congruent.
Equate the given value of ∠N and ∠K to 60° to find the value of x.
If we are using ∠N, we have,
5x – 15 = 60
5x = 60 + 15
5x = 75
$\frac{5x}{5}$ = $\frac{75}{5}$
x = 15
If we are using ∠K, we have,
4x = 60
$\frac{4x}{4}$ = $\frac{60}{4}$
x = 15
Alternative Strategy:
Another strategy for finding the value of x is to equate 5x-15 to 4x since ∠N and ∠K are congruent. Thus, we have,
5x – 15 = 4x
5x – 4x = 15
x = 15
Therefore, the value of ∠N and ∠K are both 60 degrees and x=15.
Example 8
Find the missing angle in each of the circles below.
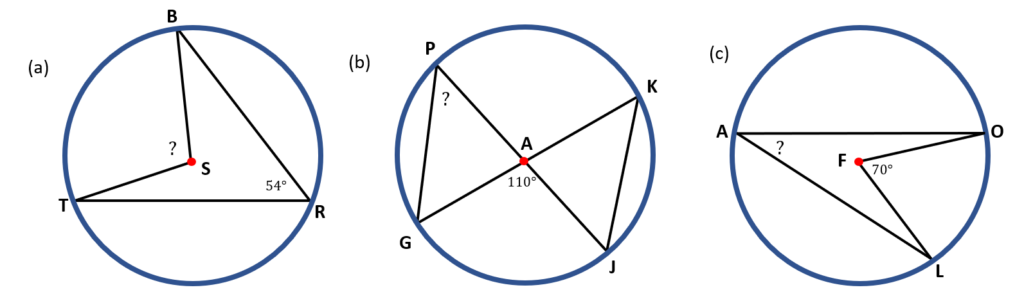
Solution:
( a ) The inscribed angle is ∠TRB, while the central angle is ∠TSB. Notice that these angles have the same intercepted arc TB. Since we are asked to get the missing angle, which is the measure of the central angle (∠TSB), we must multiply the measure of the inscribed angle (∠TRB) by 2. Hence,
∠TSB=2 (∠ TRB)
∠TSB=2 ( 54° )
∠TSB = 108°
Hence, ∠TSB measures 108 degrees.
( b ) The inscribed angle is ∠GPJ. The central angle is ∠GAJ. These angles have the same intercepted arc GJ. Since the missing angle is the inscribed angle, we must get ½ of the measure of the central angle (∠GAJ). Thus, we have,
∠GPJ = ½ ( ∠ GAJ )
∠GPJ = ½ ( 110° )
∠GPJ = $\frac{110°}{2}$
∠GPJ = 55°
Thus, ∠GPJ measures 55 degrees.
( c ) The central angle ∠LFO and the inscribed angle ∠LAO have the same intercepted arc LO. Therefore, to get the missing value, which is the inscribed angle ( ∠LAO), we must get ½ of the measure of the central angle ∠LFO.
∠LAO = ½ (∠ LFO)
∠LAO = ½ ( 70° )
∠LAO = $\frac{70°}{2}$
∠LAO = 35°
Therefore, ∠LAO measures 35 degrees.
Example 9
Find the m ∠L and m ∠F if ∠TLK is 40°.
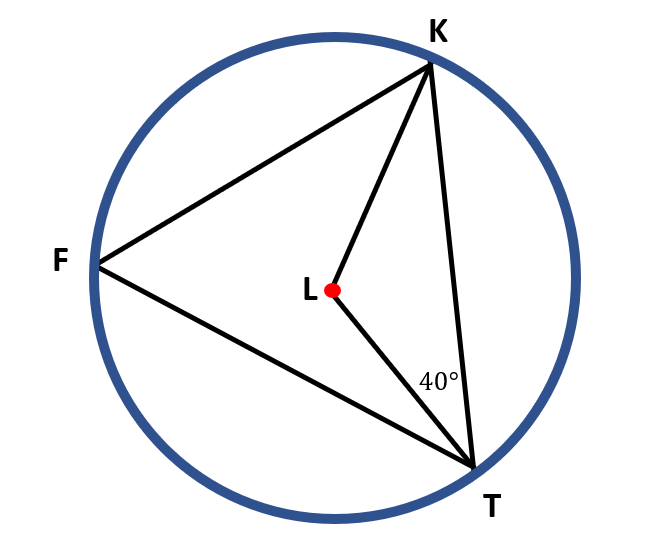
Solution
We can see that the points T, L, and K form a triangle. Since the two legs, $\overline{LT}$ and $\overline{LK}$, of the triangle are the two radii of the given circle; then ∆TLK is an isosceles triangle. Hence, we can say that ∠LKT also measures 40°.
∠L is a central angle since its vertex is at the center of the circle, and its two sides are the radii of the circle. ∠F is an inscribed angle since its vertex is on the circle and its two sides are two chords of the circle.
To find the measure of ∠L, we must remember that the sum of the interior angles of a triangle is equal to 180°. Hence, we have,
∠LKT+∠LTK+∠L = 180°
40°+40°+∠L = 180°
80°+∠L = 180°
∠L = 180°-80°
∠L = 100°
Since ∠F is an inscribed angle with the same intercepted arc as ∠L, then by the inscribed angle theorem, ∠F is ½ the measure of ∠L. Hence, we have,
∠F=½ ( ∠L )
∠F = ½ ( 100° )
∠F = $\frac{100°}{2}$
∠F = 50°
Therefore, ∠L measures 100 degrees while ∠F measures 50 degrees.
Summary
An angle is said to be inscribed if its vertex is on the circumference of the circle and both sides are chords of the same circle.
The intercepted arc is the arc that lies in the interior of an inscribed angle and has endpoints on the angle.
The term “central angle” refers to an angle whose vertex is at the center of the circle. Its measure is equal to its intercepted arc.
A chord that passes the circle’s center is referred to as the diameter.
In a triangle, the inner angles add up to 180 degrees.
An inscribed quadrilateral‘s opposite angles are supplementary angles, which means that the sum of their angle measurements equals 180 degrees.
The measure of the inscribed angle with a semi-circle intercepted arc is 90 degrees.
If two radii of a circle are the two sides of the inscribed triangle, then the triangle is isosceles.
Inscribed Angle Theorem
According to the inscribed angle theorem, the central angle’s measure is equal to double that of the inscribed angle.
β = 2θ or θ = ½ β,
where is a central angle and is an inscribed angle
Proof: Cases
Three distinct cases must be considered when proving the Inscribed Angle Theorem. These three cases cover every scenario based on the diameter’s location and the inscribed angle in the given circle.
The three cases are:
Case 1: When the diameter is one of the chords forming the inscribed angle.
Case 2: When the diameter is in the interior of the inscribed angle
Case 3: When the diameter in the exterior is the inscribed angle.
Frequently Asked Questions on Inscribed Angle Theorem ( FAQs )
What is meant by the inscribed angle theorem?
According to the inscribed angle theorem, the central angle’s measure is equal to double that of the inscribed angle.
β = 2θ or θ = ½ β
where is a central angle and is an inscribed angle
How are central angles and inscribed angles different from one another?
An angle is said to be inscribed if its vertex is on a circle and both of its sides are chords of that circle.
A central angle, on the other hand, has a vertex at the center of the circle and two radii as its sides.
For example, we have the image below with circle R and its central and inscribed angles.
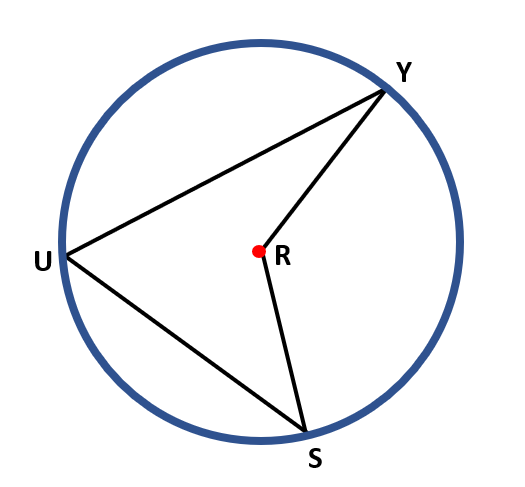
The central angle in circle R is ∠ SRY or ∠ YRS. The vertex of ∠ SRY is the center of the circle, and the two radii $\overline{RS}$ and $\overline{RY}$ are the sides.
The inscribed angle in circle R is ∠ SUY or ∠ YUS. The vertex of ∠ SUY lies on the circle, and the two chords $\overline{US}$ and $\overline{UY}$ are the sides.
What is the relationship between the central and inscribed angles?
If a central angle and an inscribed angle both intersect the same arc, the measure of the central angle would be twice that of the inscribed angle. Simply put, an inscribed angle’s measurement equals half that of the central angle.
For example, the figure below shows circle V with the measure of arc PR equaling 80°. The central angle( ∠PVR ) and the inscribed angle (∠PQR ) intersect the same arc PR, and then the measure of ∠ PVR is twice the measure of ∠ PQR.
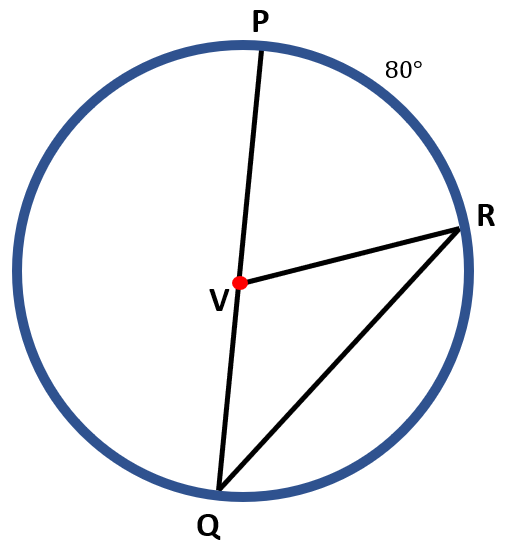
The measure of the central angle ∠ PVR=80° is the measure of its intercepted arc PR. For the measure or ∠ PQR, we have,
m ∠ PQR=½ m PR
m ∠ PQR=½ ( 80° )
m ∠ PQR = $\frac{80°}{2}$
m ∠ PQR = 40°
Therefore, m ∠ VPR=80° while m ∠ PQR=40°.
What are the cases to consider in proving the inscribed angle theorem?
Three distinct cases must be considered when proving the Inscribed Angle Theorem. These three cases cover every scenario based on the diameter’s location and the inscribed angle in the given circle.
The three cases are:
Case 1: When the diameter is one of the chords forming the inscribed angle.
Case 2: When the diameter is in the interior of the inscribed angle
Case 3: When the diameter is in the exterior of the inscribed angle.
What is the formula for getting the measurement of an inscribed angle?
The central angle’s measure is equal to twice that of the inscribed angle, according to the inscribed angle theorem.
β=2θ or θ=½ β
where is a central angle and is an inscribed angle
How do you solve inscribed angles with variables?
There are a lot of sample problems on inscribed angles that has variables. Often, we see that we will be asked to find the value of x. Let us say, for example; we have the figure below,
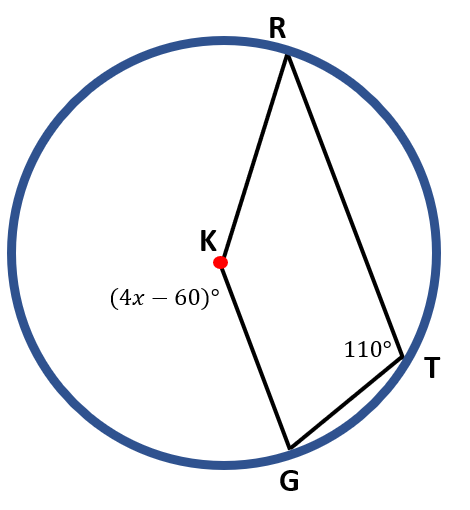
You must know the difference between a central angle and an inscribed angle. In this example, ∠GTR is the inscribed angle, while ∠GKR is the central angle.
By the inscribed angle theorem, we may find this solution and use the algebraic process to solve for the value of x. So, we have,
m ∠ GKR=2( m ∠ GTR )
m ∠ GKR=2 ( 110° )
m ∠ GKR = 220°
Let us now equate 4x+60° to 220° to find the value of x. We have,
4x + 60 = 220
4x = 220 – 60
4x = 160
$\frac{4x}{4}=\frac{160}{4}$
x=40
Therefore, the value of x is 40.
Recommended Worksheets
Inscribed Angles (National Aviation Day Themed) Math Worksheets
Complementary Angles (Lantern Festival Themed) Math Worksheets
Adjacent Angles (Mardi Gras Themed) Math Worksheets









