Introduction
A right triangle’s hypotenuse’s square length is equal to the sum of its two sides’ square lengths. This statement is called the Pythagorean Theorem and is usually expressed as
a2+b2=c2
As an illustration, we have,
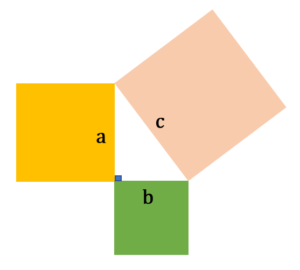
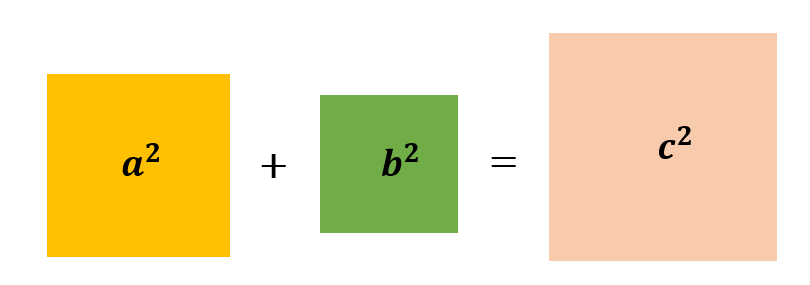
Remember that the hypotenuse is the side with length “c” while “a” and “b” are the other two sides.
This article will go through how the Pythagorean Theorem and Pythagorean Triples relate to one another. Information about Pythagorean triples and a demonstration of how to generate them are provided.
What are Pythagorean Triples?
Definition
Pythagorean triples, represented as ( a, b, c ), is a set of three positive integers that can be the sides of a right triangle. A Pythagorean triple satisfies the Pythagorean theorem equation a2+b2=c2, where “c” is the hypotenuse and “a and b” are the two legs of the right triangle.
Let us have the smallest known Pythagorean triples ( 3, 4, 5 ) as an example.
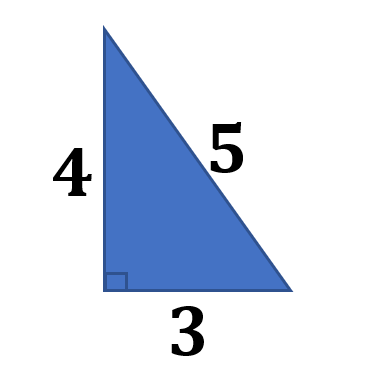
The figure shows a right-angled triangle with the Pythagorean Triples ( 3, 4, 5 ). Let us have a = 3 and b = 4 as the lengths of the two sides of the right triangle, while the longest side, c, is the hypotenuse with a distance equal to 5.
Now, using the Pythagorean Theorem, a2+b2=c2, we have,
32+42=52
9+16=25
25=25
Therefore, ( 3, 4, 5 ) is a Pythagorean Triples.
Pythagorean Triples Formula
Pythagorean triples are three positive integers that satisfy the Pythagorean Theorem:
a2+b2=c2
If a triangle has one right-angled angle, there is a relationship between the triangle’s three sides, with the longest side (called the hypotenuse) being c and the other two sides (next to the right angle) being known as a and b.
The square of the longest side is equal to the sum of the squares on the other two sides.
Generating Pythagorean Triples
Generating Pythagorean triples is possible given two positive integers, m and n, where m is greater the n or m>n. Thus, for each side of the triangle, we have,
a = m2 – n2
b = 2×m×n
c = m2 + n2
Let us these values for m and n and generate Pythagorean Triples.
( a ) m=8 , n=7
( b ) m=10, n=5
( c ) m=14, n=12
Solution:
( a ) Let us solve for a, b, and c when m=8 and n=7.
| a = m2 – n2 a = 82 – 72 a = 64-49 a=15 | b = 2×m×n b = 2×8×7 b = 112 | c=m2+n2 c=82+72 c=64+49 c=113 |
To show if ( 15, 112, 113 ) satisfy the Pythagorean Theorem,
a2+b2=c2
152+1122=1132
225+12544=12769
12769=12769
Hence, we have the Pythagorean Triples ( 15, 112, 113 ) when m = 8 and n = 7.
( b ) For m=10 and n=5
| a = m2-n2 a = 102-52 a = 100-25 a = 75 | b=2×m×n b=2×10×5 b=100 | c=m2+n2 c=102+52 c=100+25 c=125 |
Using the Pythagorean Theorem, let us substitute the generated values of a, b, and c.
a2+b2=c2
752+1002=1252
5625+10000=15625
15625=15625
Therefore, we have the Pythagorean Triples ( 75, 100, 125 ) when m = 10 and n = 5.
( c ) Solving for a,b, and c when m=14, n=12, we have,
| a = m2-n2 a = 142-122 a = 196-144 a = 52 | b=2×m×n b=2×14×12 b=336 | c=m2+n2 c=142+122 c=196+144 c=340 |
Using the Pythagorean Theorem, let us use a=52, b=336, and c=340.
a2+b2=c2
522+3362=3402
2704+112896=115600
115600=115600
Hence, we have the Pythagorean Triples ( 52, 336, 340 ) when m = 14 and n = 12.
How to Create Pythagorean Triples?
We can create Pythagorean Triples given a number. The methods below show the simple steps to use when the number is odd or even.
When the given number is odd
If n is the given odd number, then the Pythagorean Triples is ($n, \frac{n^2}{2}-\frac{1}{2},\frac{n^2}{2}+\frac{1}{2}$).
Let us say, for instance, the number 9, which is an odd number.
If n=9,
Let us substitute 9 to $n, \frac{n^2}{2}-\frac{1}{2}\:and\:\frac{n^2}{2}+\frac{1}{2}$, so we have,
| $\frac{9^2}{2}-\frac{1}{2} =\frac{81}{2}-\frac{1}{2} =\frac{80}{2} =40$ | $\frac{9^2}{2}+\frac{1}{2} =\frac{81}{2}+\frac{1}{2} =\frac{82}{2} =41$ |
By checking using the Pythagorean Theorem using a=9, b=40, and c=41.
92+402=412
81+1600=1681
1681=1681
Therefore, ( 7, 40, 41 ) are Pythagorean Triples.
Let us have another example where the odd number is n=13.
| $\frac{13^2}{2}-\frac{1}{2}=\frac{169}{2}-\frac{1}{2}=\frac{168}{2}=84$ | $\frac{13^2}{2}+\frac{1}{2}=\frac{169}{2}+\frac{1}{2}=\frac{170}{2}=85$ |
Let us check using the Pythagorean Theorem, where a=13, b=84, and c=85.
132+842=852
169+7056=7225
7225=7225
Hence, ( 13, 84, 85 ) is a Pythagorean Triple.
When the given number is even
If n is an even number, then the Pythagorean Triples is ($n,(\frac{n}{2})^2-1, (\frac{n}{2})^2+1$)
Let us say n=8, then
| $(\frac{8}{2})^2-1=(4)^2-1=16-1=15$ | $(\frac{8}{2})^2+1=\frac{64}{4}+1=16+1=17$ |
To check if ( 8, 15, 17 ) satisfy the Pythagorean Theorem, we have,
a2+b2=c2
82+152=172
64+225=289
289=289
For another example, let us have the even number n=14.
| $(\frac{14}{2})^2-1=(7)^2-1=49-1=48$ | $(\frac{14}{2})^2+1=(7)^2+1=49+1=50$ |
Using the Pythagorean Theorem to check, we have,
a2+b2=c2
142+482=502
196+2304=2500
2500=2500
Remark: The techniques give us a triple for every positive whole integer; therefore, we can see that there are infinitely many Pythagorean triples. But not all of them can be created using this technique.
Interesting Facts About Pythagorean Triples
( a ) Pythagorean Triples has three integers with either all even numbers or two odd numbers and an even number.
Some examples of Pythagorean Triples with two odd numbers and an even number are:
( 3, 4, 5 ) , ( 7, 24, 25 ) , ( 9, 40, 41), ( 13, 84, 85), ( 17, 144, 145 ), ( 21, 220, 221 ).
Some examples of Pythagorean Triples that are all even numbers are:
( 6, 8, 10 ) , ( 10, 24, 26 ) , ( 18, 80, 82 ) , ( 22, 120, 122 ), ( 30, 224, 226 ), ( 34, 288, 290 ).
( b ) There are numerous ways to find Pythagorean triples, including the Fibonacci sequence, quadratic equations, matrices, linear transformations, and others.
( c ) There are infinitely many Pythagorean Triples. For example, let us use the Pythagorean Triples below and find the resulting Pythagorean Triples when n =2, n=3, n-4, and n=5. To complete the table, the given value of n must be multiplied by each of the three numbers in the triples. Let us say, for instance, for the Pythagorean Triple ( 3, 4, 5 ); we will use ( 3n, 4n, 5n), so, if n =2, the resulting Pythagorean triple is ( 6, 8, 10 ).
| Pythagorean Triples | n = 2 | n = 3 | n = 4 | n = 5 |
| ( 3, 4 , 5 ) | ( 6, 8, 10 ) | ( 9, 12, 15 ) | ( 12, 16, 20 ) | ( 15, 20, 25 ) |
| ( 5, 12, 13 ) | ( 10, 24, 26 ) | ( 15, 36, 39 ) | ( 20, 48, 52 ) | ( 25, 60, 65 ) |
| ( 7, 24, 25 ) | ( 14, 48, 50 ) | ( 21, 72, 75 ) | ( 28, 96, 100 ) | ( 35, 120, 125 ) |
| ( 8, 15, 17 ) | ( 16, 225, 289) | ( 24, 45, 51 ) | ( 32, 60, 68 ) | ( 40, 75, 85 ) |
| ( 9, 40, 41 ) | ( 18, 80, 82 ) | ( 27, 120, 123 ) | ( 36, 160, 164 ) | (45, 200, 205 ) |
( d ) Pythagorean Triples, ( a, b, c ) satisfies the Pythagorean Theorem a2+b2=c2.
Let us say, for example, proving the Pythagorean triples ( 7, 24, 25 ) and ( 12, 16, 20).
| For (7, 24, 25 ) a2+b2=c2 72+242=252 49+576=625 625=625 | For (12, 16, 20 ) a2+b2=c2 122+162=202 144+256=400 400=400 |
Thus, the Pythagorean triples ( 7, 24, 25 ) and ( 12, 16, 20) satisfy the Pythagorean Theorem.
( e ) There are two types of Pythagorean triples, primitive and non-primitive.
Primitive Pythagorean triples are composed of three positive integers with a common factor other than 1. Usually, primitive Pythagorean triples have one even number and two odd numbers.
Some examples of primitive Pythagorean triples are ( 3, 4, 5 ), ( 5, 12, 13 ), and ( 7, 24, 25 ).
Non-primitive Pythagorean triples are composed of three positive integers with a common factor other than 1.
Some examples of non-primitive Pythagorean triples include ( 6, 8, 10 ), ( 10, 24, 26 ), ( 14, 48, 50 ), ( 16, 225, 289), and ( 18, 80, 82 ).
List of Pythagorean Triples
The table below shows examples of primitive Pythagorean Triples not greater than 1000.
| ( 3, 4, 5 ) | ( 5, 12, 13 ) | ( 7, 24, 25) | ( 8, 15, 17 ) | ( 9, 40, 41 ) |
| ( 11, 60, 61 ) | ( 12, 35, 37 ) | ( 13, 84, 85) | ( 15, 112, 113 ) | ( 16, 63, 65 ) |
| ( 17, 144, 145 ) | ( 19, 180, 181 ) | ( 20, 21, 29) | ( 20, 99, 101 ) | ( 21, 220, 221 ) |
| ( 23, 264, 265 ) | ( 24, 143, 145 ) | ( 25, 312, 313) | ( 27, 364, 365 ) | ( 28, 45, 53 ) |
| ( 28, 195, 197 ) | ( 29, 420, 421 ) | ( 31, 480, 481) | ( 32, 255, 257 ) | ( 33, 56, 65 ) |
| ( 33, 544, 545 ) | ( 35, 612, 613 ) | ( 36, 77, 85) | ( 36, 323, 325 ) | ( 37, 684, 685 ) |
| ( 39, 80, 89 ) | ( 39, 760, 761 ) | ( 40, 399, 401) | ( 41, 840, 841 ) | ( 43, 924, 925 ) |
| ( 44, 117, 125 ) | ( 44, 483, 485 ) | ( 48, 55, 73 ) | ( 48, 575, 577 ) | ( 51, 140, 149 ) |
| ( 52, 165, 173 ) | ( 52, 675, 677 ) | ( 56, 783, 785 ) | ( 57, 176, 185 ) | ( 60, 91, 109 ) |
| ( 60, 221, 229 ) | ( 60, 899, 901 ) | ( 65, 72, 97 ) | ( 68, 285, 293 ) | ( 69, 260, 269 ) |
| ( 75, 308, 317 ) | ( 76, 357, 365 ) | ( 84, 187, 205 ) | ( 84, 437, 445 ) | ( 85, 132, 157 ) |
| ( 87, 416, 425 ) | ( 88, 105, 137 ) | ( 92, 525, 533 ) | ( 93, 476, 485 ) | ( 95, 168, 193 ) |
| ( 96, 247, 265 ) | ( 100, 621, 629 ) | ( 104, 153, 185 ) | ( 105 ,208 ,233 ) | ( 105, 608, 617 ) |
| ( 108, 725, 733 ) | ( 111, 680, 689 ) | ( 115, 252, 277 ) | ( 116, 837, 845 ) | ( 119, 120, 169 ) |
| ( 120, 209, 241 ) | ( 120, 391, 409 ) | ( 123, 836, 845 ) | ( 124, 957, 965 ) | ( 129, 920, 929 ) |
| ( 132, 475, 493 ) | ( 133, 156, 205 ) | ( 135, 352, 377 ) | ( 136, 273, 305 ) | ( 140, 171, 221 ) |
| ( 145, 408, 433 ) | ( 152, 345, 377 ) | ( 155, 468, 493 ) | ( 156, 667, 685 ) | ( 160, 231, 281 ) |
| ( 161, 240, 289 ) | ( 165, 532, 557 ) | ( 168, 425, 457 ) | ( 168, 775, 793 ) | ( 175, 288, 337 ) |
| ( 180, 299, 349 ) | ( 184, 513, 545 ) | ( 185, 672, 697 ) | ( 189, 340, 389 ) | ( 195, 748, 773 ) |
| ( 200, 609, 641 ) | ( 203, 396, 445 ) | ( 204, 253, 325 ) | ( 205, 828, 853 ) | ( 207, 224, 305 ) |
| ( 215, 912, 937 ) | ( 216, 713, 745 ) | ( 217, 456, 505 ) | ( 220, 459, 509 ) | ( 225, 272, 353 ) |
| ( 228, 325, 397 ) | ( 231, 520, 569 ) | ( 232, 825, 857 ) | ( 240, 551, 601 ) | ( 248, 945, 977 ) |
| ( 252, 275, 373 ) | ( 259, 660, 709 ) | ( 260, 651, 701 ) | ( 261, 380, 461 ) | ( 273, 736, 785 ) |
| ( 276, 493, 565 ) | ( 279, 440, 521 ) | ( 280, 351, 449 ) | ( 280, 759, 809 ) | ( 287, 816, 865 ) |
| ( 297, 304, 425 ) | ( 300, 589, 661 ) | ( 301, 900, 949 ) | ( 308, 435, 533 ) | ( 315, 572, 653 ) |
| ( 319, 360, 481 ) | ( 333, 644, 725 ) | ( 336, 377, 505 ) | ( 336, 527, 625 ) | ( 341, 420, 541 ) |
| ( 348, 805, 877 ) | ( 364, 627, 725 ) | ( 368, 465, 593 ) | ( 369, 800, 881 ) | ( 372, 925, 997 ) |
| ( 385, 552, 673 ) | ( 387, 884, 965 ) | ( 396, 403, 565 ) | ( 400, 561, 689 ) | ( 407, 624, 745 ) |
| ( 420, 851, 949 ) | ( 429, 460, 629 ) | ( 429, 700, 821 ) | ( 432, 665, 793 ) | ( 451, 780, 901 ) |
| ( 455, 528, 697 ) | ( 464, 777, 905 ) | ( 468, 595, 757 ) | ( 473, 864, 985 ) | ( 481, 600, 769 ) |
| ( 504, 703, 865 ) | ( 533, 756, 925 ) | ( 540, 629, 829 ) | ( 555, 572, 797 ) | ( 580, 741, 941 ) |
| ( 615, 728, 953 ) | ( 616, 663, 905 ) | ( 696, 697, 985 ) |
More Examples
Example 1
Using the two integers 8 and 13, generate Pythagorean triples.
Solution:
Let us solve for a, b, and c when m=13 and n=8. Remember that the value m must be greater than n.
| a=132-82 a=169-64 a=64-49 a=105 | b=2×m×n b=2×13×8 b=208 | c=m2+n2 c=132+82 c=169+64 c=233 |
To show if ( 105, 208, 233 ) satisfy the Pythagorean Theorem, we have,
a2+b2=c2
1052+2082=2332
11025+43264=54289
54289=54289
Hence, we have the Pythagorean Triples ( 105, 208, 233 ) when m = 13 and n = 8.
Example 2
Show that ( 20, 21, 29 ) is a Pythagorean triple.
Solution:
Let us use the Pythagorean Theorem to show whether ( 20, 21, 29 ) is a Pythagorean triple. Remember that c must be the highest number among the three numbers.
a2+b2=c2
202+212=292
400+441=841
841=841
Example 3
Find the other numbers if one of the numbers in a Pythagorean triple is 17.
Solution:
Since 17 is an odd number, we will use ($n, \frac{n^2}{2}-12,\frac{n^2}{2}+12$) to get the Pythagorean triples where n = 17. So, we have,
| $\frac{17^2}{2}-\frac{1}{2}=\frac{289}{2}-\frac{1}{2}=\frac{288}{2}=144$ | $\frac{17^2}{2}+\frac{1}{2}=\frac{289}{2}+\frac{1}{2}=\frac{289}{2}=145$ |
Using the Pythagorean Theorem, let us confirm if ( 17, 144, 145 ) is a Pythagorean triple.
a2+b2=c2
172+1442=1452
289+20736=21025
21025=21025
Example 4
Find the value of x if ( 5, 12, x ) is a Pythagorean triple.
Solution:
Let us use the Pythagorean Theorem formula a2+b2=c2 to find the missing number. Let a = 5 and b =12. Hence, we have,
c2=a2+b2
c2=52+122
c2=25+144
c2=169
c= √169
c=13
Therefore, the Pythagorean triple is ( 5, 12, 13 ).
Example 5
Using the Pythagorean Theorem, find the value of x and determine the side lengths for Pythagorean Triples.
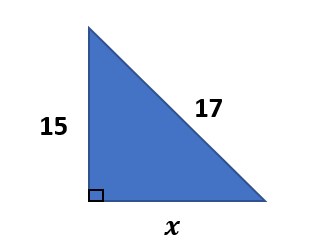
Solution:
Let us find the value of x using the Pythagorean Theorem a2+b2=c2. The hypotenuse “c” is equal to17, a = 15, and the missing number is x.
a2+b2=c2
152+b2=172
225+b2=289
225-225+b2=289-225
b2=64
b2= √64
b=8
Hence, x=8 and ( 8, 15, 17 ) is a Pythagorean Triples since all the sides of the triangle integers.
Summary
Pythagorean triples, represented as ( a, b, c ), is a set of three positive integers that can be the sides of a right triangle. A Pythagorean triple satisfies the Pythagorean theorem equation a2+b2=c2, where “c” is the hypotenuse and “a and b” are the two legs of the right triangle.
In generating Pythagorean triples given two positive integers, m and n, where m is greater the n or m>n. Thus, for each side of the triangle, we have,
a=m2-n2
b=2×m×n
c=m2+n2
A Pythagorean Triple can be created given a number.
When the given number is odd
If n is the given odd number, then the Pythagorean Triples is ($n, \frac{n^2}{2}-12,\frac{n^2}{2}+12$).
When the given number is even
If n is an even number, then the Pythagorean Triples is ($n,(\frac{n}{2})^2-1, (\frac{n}{2})^2+1$)
There are two types of Pythagorean triples, primitive and non-primitive.
Primitive Pythagorean triples are composed of three positive integers with a common factor other than 1. Usually, primitive Pythagorean triples have one even number and two odd numbers.
Non-primitive Pythagorean triples are composed of three positive integers with a common factor other than 1.
Frequently Asked Questions on Pythagorean Triples (FAQs)
What is Pythagorean Theorem?
A right triangle’s hypotenuse’s square length is equal to the sum of its two sides’ square lengths. This statement is called the Pythagorean Theorem and is usually expressed as a2+b2=c2.
Let us say, for example, that we have the right triangle below with side lengths 3, 4 and 5. The side with a length equal to 5 is the hypotenuse or the longest side, represented by the variable “c”. The other legs may be considered a = 3 and b = 4.

a2+b2=c2
32+42=52
9+16=25
25=25
How is Pythagorean Theorem related to Pythagorean Triples?
The Pythagorean Triples and Pythagorean Theorem are related. If the Pythagorean triple is given, it must satisfy the Pythagorean theorem.
For example, let us determine if ( 9, 40, 41 ) is a Pythagorean Triples.
Using the Pythagorean Theorem, a2+b2=c2, we will use c=41 since it is the highest among the three numbers. We have,
a2+b2=c2
92+402=412
81+1600=1681
1681=1681
The equation shows that the left-hand side is equal to the right-hand side. Hence, ( 9, 40, 41 ) is a Pythagorean triple.
What are the two types or categories of Pythagorean Triples?
The two types of Pythagorean Triples are primitive and non-primitive. Primitive Pythagorean triples are composed of three positive integers with a common factor other than 1. Usually, primitive Pythagorean triples have one even number and two odd numbers. Non-primitive Pythagorean triples are composed of three positive integers with a common factor other than 1.
What are the 16 primitive Pythagorean Triples less than 100?
There is a total of 16 primitive Pythagorean Triples, less than 100. Here is the list:
| ( 3, 4, 5 ) | ( 5, 12, 13 ) | ( 7, 24, 25) | ( 8, 15, 17 ) |
| ( 9, 40, 41 ) | ( 11, 60, 61 ) | ( 12, 35, 37 ) | ( 13, 84, 85) |
| ( 16, 63, 65 ) | ( 20, 21, 29) | ( 28, 45, 53 ) | ( 33, 56, 65 ) |
| ( 36, 77, 85) | ( 39, 80, 89 ) | ( 48, 55, 73 ) | ( 65, 72, 97 ) |
How do you identify if three numbers form a Pythagorean triple?
Three numbers form a Pythagorean triple if these numbers satisfy the Pythagorean Theorem, a2+b2=c2. For example, if we have ( 5, 12, 13 ), using the Pythagorean Theorem, let us have a =5, b 12, and c = 13. Remember that “c” always has the highest value. So, we have,
a2+b2=c2
52+122=132
25+144=169
169=169
It satisfies the Pythagorean theorem since the left-hand side is equal to the right-hand side of the equation. Thus, ( 5, 12, 13 ) forms a Pythagorean triple.
Recommended Worksheets
Pythagorean Theorem (Back to School Themed) Worksheets
People Series: Pythagoras (Greece Themed) Math Worksheets
Pythagorean Triples (National Hispanic Heritage Month Themed) Math Worksheets









