Introduction
We have learnt that a fraction is a number representing a part of a whole. The whole may be a single or a group of objects. Let us now learn about the addition and subtraction of like fractions. But, before that, we must recall what we mean by like fractions. Fractions that have the same denominator are called like fractions. For example, the fractions, $\frac{4}{9}, \frac{13}{9}, \frac{1}{9} and \frac{5}{9}$ are all like fractions having the common denominator 9.
We know that a number of the form $\frac{p}{q}$ or a number that can be expressed in the form of $\frac{p}{q}$, where p and q are integers and q ≠ 0 is called a rational number. So how do we define the standard form of a rational number?
It is also important to recall that a fraction is said to be in the standard form if the denominator is positive and the numerators
have no common divisor other than 1.
In order to express a given fraction in the standard form, the following steps should be followed –
Step 1 – Check whether the given number is in the form of a fraction.
Step 2 – See whether the denominator of the fraction is positive or not. If it is negative, multiply or divide the numerator as well as the denominator by -1 so that the denominator becomes positive.
Step 3 – Find the greatest common divisor (GCD) of the absolute values of the numerator and the denominator.
Step 4 – Divide the numerator and the denominator of the given fraction by the GCD (HCF) obtained in step III. The fraction so obtained is the standard form of the given fraction.
This was important to understand because, after the addition or subtraction of fractions, we will need to reduce them in the simplest form.
Now, let us learn how to add two or more like fractions.
Addition of Like Fractions
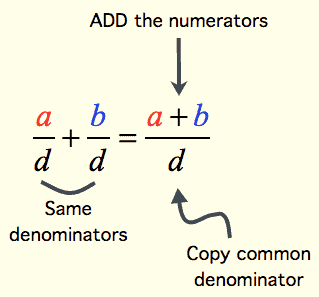
In order to add two like fractions, we follow the following steps:
- Obtain the numerators of the two given fractions and their common denominator
- Add the numerators obtained in the first step.
- Write a fraction whose numerator is the sum obtained in the second step and the denominator is the common denominator of the given fractions.
Let us understand this through an example.
Example
Suppose we want to add the fractions $\frac{3}{5}$ and $\frac{13}{5}$
Solution
Here we can see that both the fractions have the same denominator, i.e. 5.
Therefore, we go by the above-defined steps.
We check the numerators of both the fractions. They are 3 and 13.
Then, we add these numerators and get 3 + 13 = 16.
Now, we write the sum of these fractions as $\frac{16}{5}$
Hence, $\frac{3}{5} + \frac{13}{5} = \frac{16}{5}$
In order to understand the addition of like fractions in a clearer manner, let us check the graphical representation of the addition of like fractions.
Graphical Representation of Addition of Like Fractions
Before proceeding with the graphical representation of the addition of like fractions, we must recall what we mean by the graphical representation of a fraction. Let us consider the fraction $\frac{3}{4}$. This fraction is read as “three-fourth” which means three parts out of four equal parts in which a whole has been divided. Graphically, this fraction can be represented as –

Now, that we recalled how to graphically represent a fraction, let us move ahead with our discussion on the graphical representation of the addition of like fractions. We will understand it by an example.
Suppose we have the fractions, $\frac{2}{8}, \frac{3}{8} and \frac{1}{8}$ and we want to add these fractions. If we go by the steps that we have defined above for the addition of like fractions, we can see that all the three fractions have the same denominator, i.e. 8. So, in order to add these fractions, we will simply add their numerators, i.e. 2, 3 and 1. We will get 2 + 3 + 1 = 6. Therefore,
$\frac{2}{8} + \frac{3}{8} + \frac{1}{8} = \frac{6}{8}$
Now, let us represent each of these fractions, graphically.
The fraction $\frac{2}{8}$ will graphically be represented as

We can see that the above fraction has 2 shaded parts out of a total of 8 equal parts.
The fraction $\frac{3}{8}$ will graphically be represented as
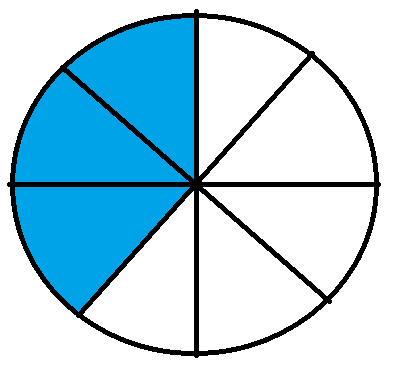
We can see that the above fraction has 3 shaded parts out of a total of 8 equal parts.
The fraction $\frac{1}{8}$ will graphically be represented as
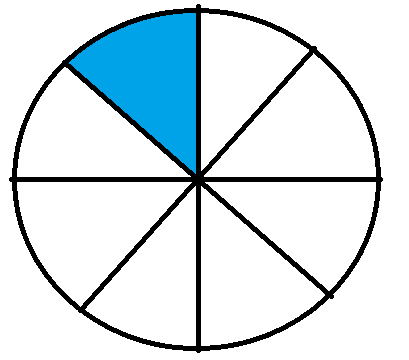
We can see that the above fraction has 1 shaded part out of a total of 8 equal parts.
If we sum up all the shaded parts in the three fractions, we can see that we will have 2 + 3 + 1 = 6 shaded parts. This will be represented graphically as –
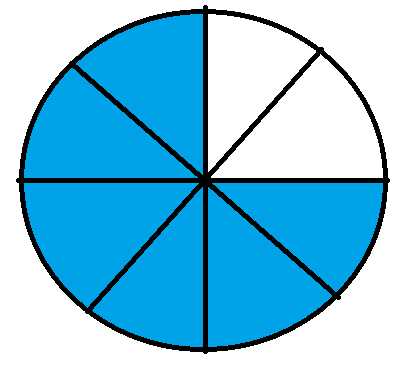
The above fraction will be written as $\frac{6}{8}$ which is the result that we had obtained after we added the three fractions above.
Now, that we have understood how to add like fractions both using steps as well as graphically, let us learn how to find the difference of two or more like fractions.
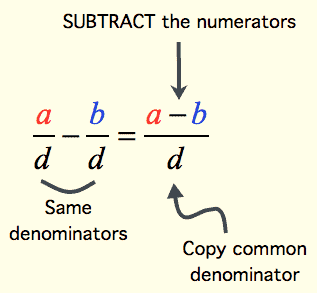
Subtraction of Like Fractions
In order to add subtract like fractions, we follow the following steps:
- Obtain the numerators of the two given fractions and their common denominator
- Subtract the subtrahend numerator from the minuend numerator obtained in the first step. Recall here that the number that is subtracted is called the subtrahend while the number from which the subtrahend is subtracted is called minuend. The result of this subtraction is called the difference.
- Write a fraction whose numerator is the sum obtained in the second step and the denominator is the common denominator of the given fractions.
Let us understand this through an example.
Example
Suppose we want to find the difference between fractions $\frac{3}{7} and \frac{1}{7}$
Solution
Here we can see that both the fractions have the same denominator, i.e. 7.
Therefore, we go by the above-defined steps.
We check the numerators of both the fractions. They are 3 and 1.
Then, we subtract 1 from 3, we will get 3 – 1 = 2
Now, we write the difference of these fractions as $\frac{2}{7}$
Hence, $\frac{3}{7} -\frac{1}{7} = \frac{2}{7}$
In order to understand the subtraction of like fractions in a clearer manner, let us check the graphical representation of subtraction of like fractions.
Graphical Representation of Subtraction of Like Fractions
Suppose we have the fractions, $\frac{5}{8} and \frac{1}{8}$ and we want to find the difference between these fractions. If we go by the steps that we have defined above for subtraction of like fractions, we can see that the two fractions have the same denominator, i.e. 8. So, in order to subtract these fractions, we will simply subtract the numerators, i.e. 5 and 1. We will get 5 – 1 = 4 Therefore,
$\frac{5}{8} – \frac{1}{8} = \frac{4}{8}$
Now, let us represent each of these fractions, graphically.
The fraction $\frac{5}{8}$ will graphically be represented as
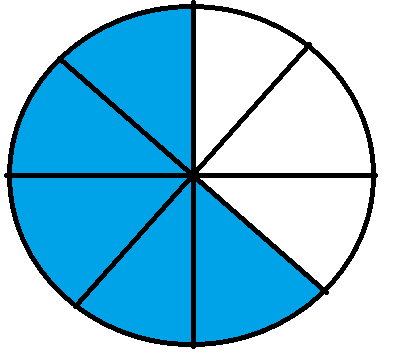
We can see that the above fraction has 5 shaded parts out of a total of 8 equal parts.
The fraction $\frac{1}{8}$ will graphically be represented as
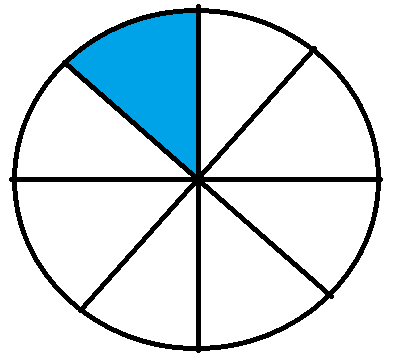
We can see that the above fraction has 1 shaded part out of a total of 8 equal parts.
If we subtract the two shaded parts in these fractions, we can see that we will have 5 – 1 = 4 shaded parts. This will be represented graphically as –
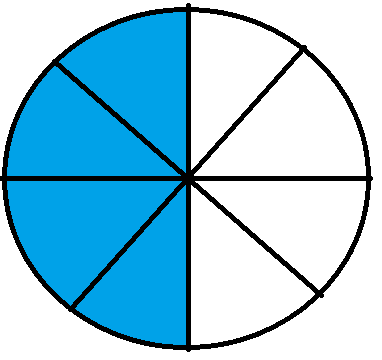
The above fraction will be written as $\frac{4}{8}$ which is the result that we had obtained after we subtracted the two fractions above.
Solved Examples
Example 1 Maria painted 1/5 of the wall space in her room. Her brother Romil helped and painted 3/5 of the wall space. How much did they paint together? How much of the room is left unpainted?
Solution We have been given that Maria painted 1/5 of the wall space in her room. Her brother Romil helped and painted 3/5 of the wall space. We are required to find out –
- How much did they paint together?
- How much of the room is left unpainted?
Let us find the above information one by one.
First of all, we need to understand the fractions given to us. We have,
Fraction of wall space painted by Maria = 1/5
Fraction of wall space painted by Romil = 3/5
It can be clearly seen that both the fractional values have the same denominator. Therefore the first thing to be noticed is that they are like fractions. Now in order to find out how much they painted together, we will have to find the sum of these fractions. Since they are like fractions, we just need to add the numerators of the fractions as we have learnt above. Therefore, we have,
Wall space painted by both = 1/5 + 3/5
= (1+3)/5 = 4/5
Therefore, the wall space painted by them together = 4/5 which is the answer to the first problem.
Now, let us consider the second problem, how much of the room is left unpainted? To find the answer to this question we need to subtract the fraction of the wall painted from the total wall pace. We have,
Here, the total wall space will be 1 as it is a whole.
Also, we have already found that the wall space painted by Maria and Romil together = 4/5
Therefore
Wall Space left to be painted = Total wall space – Wall space painted
We get the unpainted space = (5 – 4)/ 5 = 1/5
Therefore, Maria and Romil painted 4/5 of the wall space together and the room space left unpainted is 1/5.
Example 2 Daniel bought 2 ½ kg sugar whereas Sam bought 3 ½ kg of sugar. Find the total amount of sugar bought by both of them.
Solution We have been given that Daniel bought 2 ½ kg of sugar whereas Sam bought 3 ½ kg of sugar. We are required to find the total amount of sugar bought by both of them.
To find the answer to the above problem, let us first understand the fraction values given to us.
Sugar bought by Daniel = 2 ½ Kg
Sugar bought by Sam = 3 ½ kg
It can be clearly seen that both the fractional values have the same denominator, i,e 2. Therefore the first thing to be noticed is that they are like fractions.
Now, to find the value of the total sugar bought by them, we will need to add the two fractions. We shall proceed with adding these fractions by adding the numerators as we have learnt above.
But, before, that, it is important to understand that the given fractions are mixed fractions. We will first need to convert them to improper fractions. Therefore,
2 ½ kg = 5/2 kg and 3 ½ kg = 7/2 kg
So the total sugar bought by both of them = Sugar bought by Daniel + Sugar bought by Sam
Now, adding their numerators we have, 5 + 7 = 12
Therefore, 5 / 2 + 7 / 2 = 12 / 2 = 6 kg
Hence, Daniel and Sam together bought 6 kg of sugar.
Example 3 Add the fractions $\frac{5}{30} + \frac{7}{30}$
Solution We have been given the fractions $\frac{5}{30} and \frac{7}{30}$. we are required to find their sum.
It can be clearly seen that both the fractional values have the same denominator, i.e. 30. Therefore the first thing to be noticed is that they are like fractions.
The first thing that we need to do now is to add the numerators of both the fractions.
We will get, 5 + 7 = 12
Therefore, $\frac{5}{30} + \frac{7}{30} = \frac{12}{30}$
The above answer can further be simplified by looking at the numerator and the denominator of the fraction. We can see that the numerator and the denominator of the fraction are both divisible by 2 and 6. However, we always want the largest common divisor to reduce the fraction to its lowest term.
Therefore, let us find the largest common divisor of 12 and 30.
We know that
12 = 2 x 2 x 3
30 = 2 x 3 x 5
From the above, we can see that the largest common divisor of the two numbers, 12 and 30 = 6
Dividing both the numerator and the denominator by 6, we get,
$\frac{12}{30} = \frac{12 ÷6}{30 ÷6} = \frac{2}{5}$ which is in its simplest form.
Hence, $\frac{5}{30} + \frac{7}{30} = \frac{2}{5}$
Example 4 Subtract the fractions $\frac{10}{27} – \frac{4}{27}$
Solution We have been given the fractions $\frac{10}{27} and \frac{4}{27}$ and we are required to find their difference.
It can be clearly seen that both the fractional values have the same denominator, i.e. 27. Therefore the first thing to be noticed is that they are like fractions. So, the two fractions have the same denominators which mean we should be able to easily subtract their numerators.
$\frac{10}{27} – \frac{4}{27} = \frac{10-4}{27} = \frac{6}{27}$
The above answer can further be simplified by looking at the numerator and the denominator of the fraction. We can see that the numerator and the denominator of the fraction are both divisible by 3. However, we always want to ensure that we use the largest common divisor to reduce the fraction to its lowest term.
Therefore, let us find the largest common divisor of 6 and 27
We know that
6 = 2 x 3
27 = 3 x 3 x 3
From the above, we can see that the largest common divisor of the two numbers, 6 and 27 = 3
Dividing both the numerator and the denominator by 3, we get,
$\frac{6}{27} = \frac{6 ÷3}{27 ÷3} = \frac{2}{9}$ which is in its simplest form.
Therefore, $\frac{10}{27} – \frac{4}{27} = \frac{2}{9}$
Example 5 Subtract the fractions $\frac{21}{81} and \frac{3}{81}$
Solution Since the denominators of the two fractions are equal, subtract their numerators and copy the common denominator. We will get,
$\frac{21}{81} – \frac{3}{81} = \frac{21-3}{81} = \frac{18}{81}$
The above answer can further be simplified by looking at the numerator and the denominator of the fraction. We can see that the numerator and the denominator of the fraction are both divisible by 3. However, we always want the largest common divisor to reduce the fraction to its lowest term.
Therefore, let us find the largest common divisor of 18 and 81
We know that
18 = 3 x 2 x 3
81 = 3 x 3 x 3 x 3
From the above, we can see that the largest common divisor of the two numbers, 18 and 81 = 9
Dividing both the numerator and the denominator by 9, we get,
$\frac{18}{81} = \frac{18 ÷9}{81 ÷9} = \frac{2}{9}$
Hence, $\frac{21}{81} – \frac{3}{81} = \frac{2}{9}$
Key Facts and Summary
- A fraction is a number representing a part of a whole. The whole may be a single or a group of objects.
- Fractions that have the same denominator are called like fractions.
- A fraction is said to be in the standard form if the denominator is positive and the numerators have no common divisor other than 1.
- To reduce a fraction to its simplest form Find the greatest common divisor (GCD) of the absolute values of the numerator and the denominator. Divide the numerator and the denominator of the given fraction by the GCD (HCF) obtained in step III. The fraction so obtained is the standard form of the given fraction.
- The number that is subtracted is called the subtrahend while the number from which the subtrahend is subtracted is called minuend. The result of this subtraction is called the difference.
Recommended Worksheets
Multiplication and Division of Fractions (Veterans’ Day Themed) Math Worksheets
Dot Plots/Line Plots with Fractional Units (Snacks and Beverages Themed) Math Worksheets
Comparing Like Fractions Math Worksheets









