Introduction
Ratios hold a prominent place in the world of mathematics. We use different ratios in everyday life for the purpose of carrying out various measurements. One such ratio is the golden ratio. What is golden ratio and what is its significance? Let us find out.
Definition
The golden ratio is the ratio of two numbers such that their ratio is equal to the ratio of their sum to the larger of the two quantities. In other words, two quantities are said to be in golden ratio, if their ratio is equal to the ratio of their sum to the larger of the two quantities. The Golden Ratio was first discovered in the 1500s and was called “The Divine Proportion” in a book of the same title by Luca Pacioli. Therefore, the golden ratio is also known as the golden mean, golden section or divine proportion. It is also believed that the first person to officially name and define the Golden Ratio was the mathematician Euclid, in his treatise ‘Elements’ (written around 300BC), although the earlier mathematician Hippasus was the first to identify that the Golden Ratio wasn’t a whole number.
Symbol for Golden Ratio
The golden ratio is often represented using the symbol “ϕ” (phi).
Approximate Value of Golden Ratio
The approximate value of the golden ratio is 16.18.
Let us understand the golden ratio through an example.
Let “ a “ and “ b” be two quantities such that a and b are both positive numbers, i.e. a > b > 0, then the golden ratio of and b will be represented as –
$\frac{a}{b} = \frac{a+b}{a}$ = ϕ
Solving the above equation, we get,
a2 – ab – b2 = 0
The solution, ϕ to the above equation will be an irrational number such that
ϕ = $\frac{-1+ \sqrt{5}}{2}$ = 1.618033988 . . . . . . . . . . . . . .
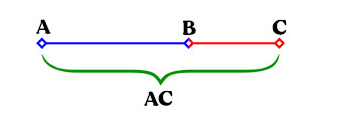
Consider the above figure. In this figure, we can see line segment AB and line segment BC. The ratio of the length of AB to AC is ϕ, which is the Golden Ratio. However, the ratio of segment BC to the whole segment AC is also ϕ.
Why Golden Ratio is considered so important?
The golden ratio is not just a factor obtained for a quadratic equation that has an irrational number as a solution. It is much more than this. The golden ratio is considered important for designing purposes with even the great artists such as Leonardo a Vinci having used the golden ratio in his art work. It is also believed that using the golden ratio can be useful to create the most pleasing and visually attractive shapes even the Parthenon in Athens, Greece is believed to have been built on the calculations based on the golden ratio. Some other examples include The Farnsworth House in the USA, The Great Stupa at Borobudur in Indonesia and The assorted works of Piet Mondrian. Not just this, one can simply create a simple design using a golden ratio.
Formula for Golden Ratio
Let us now discuss the formula for the golden ratio.
We have learnt above that if “ a “ and “ b” are two quantities such that a and b are both positive numbers, i.e. a > b > 0, then the golden ratio of and b will be represented as –
$\frac{a}{b} = \frac{a+b}{a}$ = ϕ . . . . . . . . . . . . . . . . . . . ( 1 )
Now, from the above equation, two more equations can be derived. These equations are –
$\frac{a}{b}$ = ϕ . . . . . . . . . . . . . . . . . . . . . . . . . ( 2 )
$\frac{a+b}{a}$ = ϕ . . . . . . . . . . . . . . . . . . . . . . . . 3 )
If we carefully observe the equation 2, we can see that this equation can also be written as –
$\frac{a}{a} + \frac{b}{a}$ = ϕ
This can equation can further be simplified to be written as –
1 + $\frac{b}{a}$ = ϕ . . . . . . . . . . . . . . . . . . . . . . . ( 4 )
Now, if we observe the equation ( 1 ), we can say that –
$\frac{a}{b}$ = ϕ therefore ,
$\frac{b}{a} = \frac{1}{ϕ}$ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 5 )
Substituting the above values obtained in the equation ( 4 ), we get
1 + $\frac{1}{ϕ}$ = ϕ which is the formula for the golden ratio.
Hence, the formula for the golden ratio is given by 1 + $\frac{1}{ϕ}$ = ϕ
Let us now leant how the value of the golden ratio has been derived.
Derivation for the Golden Ratio Value
We have learnt above that the formula for the golden ratio is given by
1 + $\frac{1}{ϕ}$ = ϕ . . . . . . . . . . . . . . . . . . . . . . . ( 1 )
⇒ ϕ + 1 = ϕ2
The above equation can be rearranged to written as –
ϕ2 – ϕ – 1 = 0 . . . . . . . . . . . . . . . . . . . ( 2 )
Now, the above equation is a quadratic equation of the form a x 2 + b x + c = 0
We know that in order to solve quadratic equation, we use the following formula –
x = $\frac{-b±\sqrt{b^2-4ac}}{2 a}$ . . . . . . . . . . . . . . . . . . . ( 3 )
From equation ( 1 ) we have,
x = ϕ, a = 1, b = – 1 and c = – 1
Substituting these values in the equation ( 3 ) we get,
ϕ = $\frac{- (-1) ± \sqrt{( -1 )^2-4 x (1) x ( -1 )}}{2 x ( 1 )} = \frac{1± \sqrt{1+4}}{2} = \frac{1± \sqrt{5}}{2}$
Thus, two solutions that can be obtained by solving the above equation are –
ϕ = $\frac{1 + \sqrt{5}}{2}$ . . . . . . . . . . . . . . . ( 4 ) and
ϕ = $\frac{1 – \sqrt{5}}{2}$ . . . . . . . . . . . . . . . ( 5 )
Simplifying the equations ( 4 ) and ( 5 ) we will get
ϕ = 1.618033 . . . . . . . . . . and
ϕ = – 1.618033 . . . . . . . . . .
Now, it is important to recall here that by the basic definition of the golden ratio is has to a ratio between two positive values. This means that the golden ratio cannot be a negative number. Hence, we shall discard the negative value of that we have obtained above. Thus we are left with one value of which is 1.618033 . . . . . . . . . .
Hence, the golden ratio is approximately equal to 1.618033 . . . . . . . . . . . . . . .
Let us now recall another series that is widely used in mathematics, i.e. Fibonacci series. Is there any relation between the golden ratio and the Fibonacci series? Let us find out.
Relation between Golden ratio and Fibonacci Series
Let us first recall what we mean by the Fibonacci series. We know that the Fibonacci sequence is a special type of sequence in which each term in the sequence is obtained by adding the sum of two previous terms. The Fibonacci series was named after an Italian mathematician named Leonardo Pisano Bogollo, who was later known as Fibonacci. The Fibonacci series is the sequence of numbers which are also known as Fibonacci numbers, where every number is sum of the preceding two numbers, such that the first two terms are ‘ 0 ‘ and ‘ 1 ‘. The formula to find the Fibonacci series can be given to express the ( n + 1 ) t h term in the sequence is defined using the recursive formula, such that F o = 0, F 1 = 1, to give F n. For example, let us take the first two terms 0 and 1, then the third term is obtained by adding 0 and 1, which is equal to 1. The fourth term is found by adding the second term and third term ( i.e. 1 + 1 = 2 ), and so on. Hence, the Fibonacci sequence is 0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , . . . . . . . . . . . . . .
Can we say that there exists a relation between the golden ratio and the Fibonacci series? Yes, there does exist a special relation between the golden ratio and the Fibonacci series. What is this relation? Let us find out.
Let us consider two successive terms of the Fibonacci series. If we carefully observe the ratio of these two terms, we will find that this ratio is very close to the golden ratio. If we take two large numbers which are successive terms of the Fibonacci series, we will find that this ratio is very close to the golden ratio. For better understanding, let us place the successive values of the Fibonacci series in the form of a table and find their ratios. We will have,
| Term 1 | Term 2 | Ratio = Term 1 / Term 2 |
| 2 | 3 | 1 . 5 |
| 3 | 5 | 1 . 6 6 6 6 6 6 6 . . . . . |
| 5 | 8 | 1 . 6 |
| 8 | 13 | 1 . 6 2 5 |
| 13 | 21 | 1 . 6 1 5 3 8 4 6 . . . . . . |
| 21 | 34 | 1 . 6 1 9 0 4 7 6 . . . . . . . . . |
| 34 | 55 | 1 . 6 1 7 6 4 7 0 5 . . . . . . . |
| 55 | 89 | 1 . 6 1 8 1 8 1 8 . . . . . . . |
| 89 | 144 | 1 . 6 1 7 9 7 7 5 2 . . . . . . |
From the above values we can see that the ratio of successive terms of the Fibonacci series is very close to the golden ratio.
Golden Rectangle
Similar to the golden ratio, we have a golden rectangle as well. Let us consider a rectangle assuming that its sides satisfy the golden ratio. Such a rectangle is called a golden rectangle. We then add a line segment in the rectangle that separates the rectangle into a perfect square while creating another rectangle as well. This news rectangle is the golden rectangle. Thus, a golden rectangle again consists of a square and a smaller rectangle, which is itself a golden rectangle.
If we repeat this process and draw a curve through the successive squares, we obtain a golden spiral. The spiral thus obtained is a spiral whose logarithmic growth curve is . now let us consider another geometric figure which is known as a regular pentagon. We know that a regular pentagon is a shape that is made of 5 edges. Suppose we have a regular pentagon having a side “ a “ . We then draw diagonals within the pentagon. The length of these diagonals will be a . .
Real Life Applications of Golden Ratio
The golden ratio is not just a standalone formula to be used for mathematical calculations. It has been widely used in real life situations as well. Some of these areas where we find the application of the golden ratio are –
- The golden ratio is found in different arts, architecture and designs.
- The designs of famous structures such as The Great Pyramid of Egypt and the Parthenon have either been partially or completely based on the concept of the golden ratio.
- In the 1500s the golden ratio was also known as the “ Divine Proportion “.
- Great artists like Leonardo Da Vinci used the golden ratio in a few of his masterpieces.
- Even the human face has proportions that are approximately the Golden Ratio, so beauty experts rely on it to create aesthetically pleasing looks.
- The standard widescreen aspect ratio for televisions and monitors is about 1.7, which is pretty close to the golden ratio.
- Many houses have rooms whose dimensions obey the Golden Ratio.
- In modern mathematics, the golden ratio occurs in the description of fractals, figures that exhibit self-similarity and play an important role in the study of chaos and dynamical systems.
Golden Ratio in Human Body
It is not only the objects and monuments where we find the use as well as applications of the golden ratio. The golden ratio can be observed in the human body as well. In fact, the centre of many proportions in the human body happens to be the golden ratio. The shape of the human face as well as the ratio of the height of the navel to the height of the body is all based on the golden ratio. There are many possible ratios of the human body, with the ideal one being assumed the one that obeys the golden ratio.
Key Facts and Summary
- The golden ratio is the ratio of two numbers such that their ratio is equal to the ratio of their sum to the larger of the two quantities.
- The golden ratio is often represented using the symbol “ϕ” (phi).
- The approximate value of the golden ratio is 16.18.
- Let “ a “ and “ b” be two quantities such that a and b are both positive numbers, i.e. a > b > 0, then the golden ratio of and b will be represented as – $\frac{a}{b} = \frac{a+b}{a}$ = ϕ.
- The formula for the golden ratio is given by 1 + $\frac{1}{ϕ}$ = ϕ.
- The ratio of successive terms of the Fibonacci series is very close to the golden ratio.
- Similar to the golden ratio, we have a golden rectangle as well. Let us consider a rectangle assuming that its sides satisfy the golden ratio. Such a rectangle is called a golden rectangle.
- The golden ratio is not just a stand alone formula to be used for mathematical calculations. It has been widely used in real life situations as well.
- The designs of famous structures such as The Great Pyramid of Egypt and the Parthenon have either been partially or completely based on the concept of the golden ratio.
- In the 1500s the golden ratio was also known as the “ Divine Proportion “.
- Great artists like Leonardo Da Vinci are believed to have used the golden ratio in a few of his masterpieces.
Recommended Worksheets
Ratio and Proportion (Armistice Day Themed) Math Worksheets
Understanding Ratio between Two Quantities 6th Grade Math Worksheets
Solving Proportional Relationships Between Two Quantities 7th Grade Math Worksheets









