Introduction
We often compare a lot of things in our daily life. While there may be similarities in some objects, they would also have their share of differences. Similarly, in maths as well, we find difference between numbers. Finding difference is one of the four major mathematical operations in mathematics, the other three being adding, multiplying and dividing of numbers. Do, what do we mean by difference in maths? Let us find out.
Definition
Difference is the result of subtracting one number from another. The process of finding the difference is also known as subtraction. In other words, it is the process of taking away a number from another. Key terms of this process are –
Subtrahend – The number that is subtracted is called the subtrahend
Minuend – The number from which the subtrahend is subtracted is called minuend.
Difference – The result of this subtraction is called the difference.
Now, that we know the meaning of difference let us learn how to write it in symbolic form.
Symbol
The symbol used for showing difference of two numbers is ( – ).
The formula for finding the difference between two numbers is
Minuend – Subtrahend = Difference
For example, you had 10 pencils. Your sister borrowed 6 pencils from you. So, how many pencils were you left with? You were left with 4 pencils. How did we get the number 4?
We will find the difference to obtain the number of pencils left with you.
Mathematically, the above problem can be represented as
Number of pencils you had = 10
Number of pencils your sister borrowed from you = 6
Number of pencils left with you = 10 – 6 = 4
Here 10 is the minuend, i.e. the number from which another number is being subtracted.
6 is the subtrahend, i.e. the number that is being subtracted.
Now, that we know how to represent the difference in mathematical form, let us learn how to find the difference between two numbers.
How to Find Difference
The method of finding the difference between two numbers depends upon the type of numbers between which difference is to be found. Let us learn about finding differences between some sets of numbers.
Finding Difference between Natural Number or Whole Numbers
The following are the steps involved in finding the Difference between Natural numbers or Whole Numbers –
1. Place the values vertically in order of their place values.
2. Start subtracting the numbers, starting from the one’s place.
Let us understand it using an example.
Example
Suppose we wish to find the difference between 123 from 658. Both are three-digit numbers, therefore placing one number below the other in order of their place values, we get –
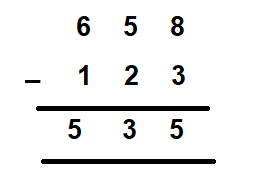
In the above case we saw that each digit of the subtrahend was less than the corresponding digit in the minuend. How would we subtract a subtrahend that is greater at a certain place value than the corresponding value of the minuend?
Let us understand it using an example.
Example
Suppose, we wish to find the difference between 2356 from 7814. Compare the corresponding digits of both the subtrahend and the minuend. You will notice that the value of subtrahend is larger than the value of the minuend at some places. So, how do we subtract 4 from 6? We use the concept of borrowing in such cases. This means that we borrow 1 from the next number in the place value.
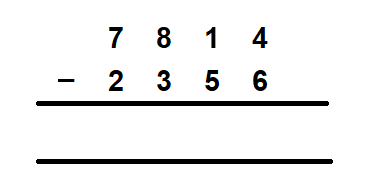
Let us solve this step by step.
- Subtract 6 from 4. We cannot larger numbers, so we borrow 1 from the digit that is at the ten’s place in the minuend. In this case, the number is 1. So we borrow 1 from 1, and the 1 at the ten’s place in the minuend becomes 0. But the number at the one’s place of the minuend, after borrowing 1 becomes 14. Now we can subtract 6 from 14 and we get 8 at the one’s place as the answer.
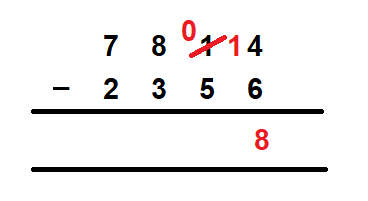
- Next, we move to subtract the digits at the ten’s place. Remember, the digit at the ten’s place is now 0, instead of the 1 that we had earlier. So, we need to subtract 5 from 0, which again is not possible. Therefore, we repeat the steps again that we did for subtracting the digits at the one’s place. We will borrow 1 from the digit at the hundred’s place, and give it to 0 at the ten’s place. So, 8 at the hundred’s place of the minuend becomes 7 and the 0 at the ten’s place of the minuend becomes 10. Now we can subtract 5 from 10 and we get 5 as the answer at the ten’s place.
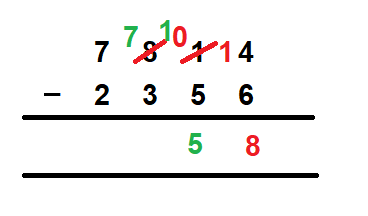
- Next, we look at the values at the hundred’s place. Here, we have 3 as the subtrahend and 7 as the minuend which can be easily subtracted. So, we get 4 as the answer at the hundred’s place.
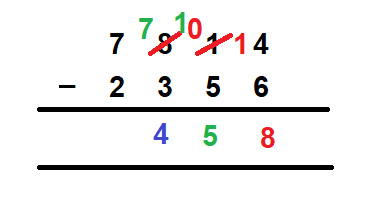
- Last, we check the values at the thousand’s place. We have 2 as the subtrahend and 7 as the minuend. Hence, we get 5 as the answer at the thousand’s place.

Hence, 7814 – 2356 = 5458
Finding Difference between Decimal Numbers
To find the difference between decimal numbers, the below steps are followed –
- Change to like decimals.
- Line up the decimal points, that is the decimal numbers are placed one below the other such that the tens digit is below tens, ones is below ones, the decimal point is below the decimal point, the tenth digit is below the tenth digit, the hundredth digit is below the hundredth digit and so on.
- Subtract as in case of the whole number, Borrow wherever necessary.
- Place the decimal point in the difference directly below the decimal point in the decimal numbers.
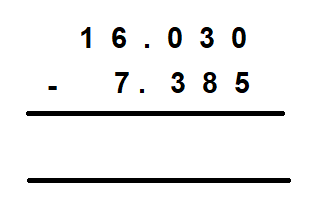
For example, let us subtract 7.385 from 16.03
Step 1 – Converting to Like Decimals
We don’t make any changes to 7.385 but re-write 16.03 as 16.030
Step 2 – Line up the decimal points
We have,
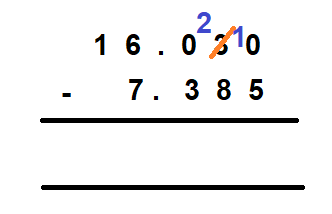
Step 3 – Subtract the thousandths.
You cannot subtract 5 thousandths from 0 thousandths. Therefore, you need to borrow 1 from hundredths.
You have 3 at the hundredth’s place. Borrow 1 from 3 which now becomes 2. The 1 that you have borrowed from 3 goes to 0 at the thousandth place which now becomes 10.
Now you can subtract 5 from 10 and you get 5 as the difference at the thousandth place.
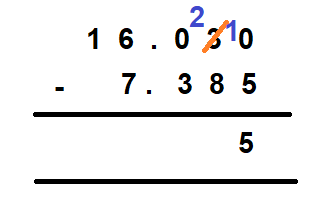
Step 4 – Subtract the hundredth’s place
You cannot subtract 8 hundredths from 2 at the hundredths place. Therefore, you need to borrow 1 from the tenth’s place.
But, you have 0 at the tenth’s place which means it has nothing to give it to you. So, you move on to the one’s place where you have 6.
Now, the borrowing of numbers will be completed in two steps.
- First, from 6 at one’s place, you borrow 1 and give it to 0. The 6 at one’s place becomes 5 and the 0 at the tenth place becomes 10.
- Now, that 0 at the tenth’s place has become 10, it can give 1 to the number 2 at the hundredth’s place. So, on borrowing 1 from 10 at tenth’s place, the number at tenth’s place becomes 9 and the number at hundredth’s place becomes 12.
Now you can subtract 8 from 12 and you get 4 as the difference at the hundredth’s place.
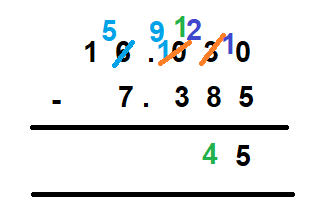
Step 5 – Subtract the tenth’s place.
After the last borrowing, the number at the tenth’s place is 9 which is greater than 3. Hence 3, upon being subtracted from 9 will be 6 as the difference at the tenth’s place.
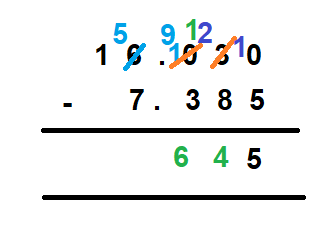
Step 6 – Subtract the one’s place
You have 5 at the one place which is smaller than 7. Hence it is not possible to subtract 7 from 5. Now, check the digits at the ten’s place. It is 1. Borrow 1 from this digit. The digit at the ten’s place becomes 0, while the digit at the one’s place becomes 15 which is now greater than 7.
Now, subtract 7 from 15 and you get 8 as the difference at the one’s place.
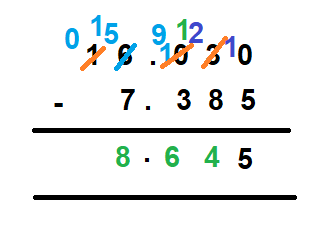
Step 7 – Subtract the ten’s place.
The number at the ten’s place is 0 and there is nothing to subtract as well. So, you may leave it as it is or just write 0 as the difference.
Finding Difference between Fractions
The following steps are following for finding the difference between fractions –
- Obtain the fractions and their denominators. Check whether the denominators of the fractions are same or not. If the denominators are same, go to Step 4, else go to Step 2.
- In case the denominators are different, find the Least Common Multiple ( L.C.M) of the denominators. In other words, make the denominators the same by finding the Least Common Multiple (LCM) of their denominators. This step is exactly the same as finding the Least Common Denominator (LCD).
- Convert each function into an equivalent fraction having the same denominator equal to the L.C.M obtained in the previous step. This means that you need to rewrite each fraction into its equivalent fraction with a denominator that is equal to the Least Common Multiple that you found in the previous step.
- Since the fractions are now like fractions, subtract them as we do for a like fraction, i.e. subtract their numerators.
- Reduce the fraction to its simplest form, if required.
Let us understand the above steps through an example.
Example
Solve $\frac{33}{4} – \frac{17}{6}$
Solution
We have been given the fractions, $\frac{33}{4}\:and\:\frac{17}{6}$.
We can clearly see that the denominators of these fractions are different. Therefore, we will proceed according to the steps defined above to obtain their difference.
We will first find the L.C.M of 4 and 6
L.C.M of 4 and 6 = 12
So, we will convert the given fractions into equivalent fractions with denominator 12.
We will get,
$\frac{33}{4} = \frac{33 x 3}{4 x 3} = \frac{99}{12}$
Similarly,
$\frac{17}{6} = \frac{17 x 2}{6 x 2} = \frac{34}{12}$
Now, we two fractions, $\frac{99}{12}$ and $\frac{34}{12}$ which have a common denominator 12 and are thus like fractions. So, we will subtract their numerators to get,
$\frac{99}{12} – \frac{34}{12} = \frac{99- 34}{12} = \frac{65}{12}$
Hence, $\frac{33}{4} – \frac{17}{6} = \frac{65}{12}$
Using Difference for Comparison
Another way in which we use the difference is to compare different types of numbers. Let us learn about the difference between important mathematics terms.
Difference between Natural Numbers and Whole Numbers
| Natural Numbers | Whole Numbers |
| Natural numbers are defined as the basic counting numbers. | Whole numbers are defined as the set of natural numbers, and it started with zero. |
| Natural Numbers are represented using the letter “N” | Whole Numbers are represented using the letter “W”. |
| Natural numbers start from 1 | Whole Numbers start from 0 |
Difference between Fractions and Rational Numbers
| Fractions | Rational Numbers |
| Fractions are written in the form of a/b, where a and b are whole numbers, and b ≠ 0 | Rational Numbers are Written in the form of p/q, where p and q are integers, and q ≠ 0 |
| All fractional numbers are rational numbers | All rational numbers are not fractions. |
| Example 2/3, 5/6 | Example 2/-7, 5/3 |
Difference between Area and Perimeter
| Area | Perimeter |
| The area is the region occupied by a closed shape in a two-dimensional plane. | Perimeter is the length of the outer boundary of a closed shape |
| It is measured in square units | It is measured in units |
| Example: Area of a lawn | Example : Perimeter of a playground |
Examples
Example 1 A recipe needs 3/7 teaspoon black pepper and 1/4 teaspoon red pepper. How much more black pepper does the recipe need?
Solution We have been given that a recipe needs 3/7 teaspoon black pepper and 1/4 teaspoon red pepper. We need to find out how much more black pepper is required in the recipe as compared to red pepper.
First of all, we will summarise the fractions given to us. We have,
Fraction of black pepper needed in the recipe = $\frac{3}{7}$
Fraction of red pepper needed in the recipe = $\frac{1}{4}$
In order to find out how much more black pepper is required in the recipe as compared to red pepper, we will need to find the difference between the black pepper and the red pepper used.
Therefore, we need to find out the value of $\frac{3}{7} – \frac{1}{4}$
The denominators of the above fractions are different; therefore, we will find their L.C.M first.
L.C.M of 7 and 4 = 28
Now, we will convert the given fractions into equivalent fractions with denominator 28.
$\frac{3}{7} = \frac{3 x 4}{7 x 4} = \frac{12}{28}$
$\frac{1}{4} = \frac{1 x 7}{4 x 7} = \frac{7}{28}$
Now, that the denominator of both the fractions is the same we will find the difference in their numerators. We have,
$\frac{3}{7} – \frac{1}{4} = \frac{12}{28} – \frac{7}{28} = \frac{12- 7}{28} = \frac{5}{28}$
Hence, the amount of more black pepper required in the recipe as compared to red pepper = $\frac{5}{28}$
Example 2 Samina purchased a syrup for £ 36.00, a cookies box for £ 29.50 and a hair oil bottle for £ 32.50. She gave the shopkeeper £ 100, how much money did the shopkeeper return as balance?
Solution We have been given that Samina purchased a syrup for £ 36.00, a cookies box for £ 29.50 and a hair oil bottle for £ 32.50. She gave the shopkeeper £ 100. We are required to find the money returned by the shopkeeper as a balance. In order to do so, first, let us summarise the items purchased by Samina.
Cost of syrup purchased by Samina = £ 36.00
Cost of cookies box purchased by Samina = £ 29.50
Cost of hair oil bottle purchased by Samina = £ 32.50
Total shopping by Samina = £ 36.00 + £ 29.50 + £ 32.50 = £ 98
Now, Samina gave £ 100 to the shopkeeper. Therefore
Change returned by the shopkeeper = £ 100 – £ 98 = £ 2.00
Hence, Samina got £ 2.00 from the shopkeeper as a change.
Example 3 Peter had £7.45 from his pocket money. He used it to buy candies for £5.30. How much pocket money was he left with?
Solution We have been given that, Peter had £7.45 from his pocket money. He used it to buy candies for £5.30.
In order to find out the pocket money he was left with, we will need to find the difference in the given values. Therefore, we have
Total pocket money with Peter = £7.45
Money Peter spent on buying candies = £5.30
Pocket money left with Peter = £7.45- £5.30
7 . 4 5
– 5 . 3 0
———–
2 . 1 5
Hence, Peter is left with £2.15 pocket money.
Key Facts and Summary
- Difference is the result of subtracting one number from another. The process of finding the difference is also known as subtraction.
- The symbol used for showing difference of two numbers is ( – ).
- For finding the difference between two or more natural numbers or whole numbers, we place the values vertically in order of their place values. then we subtract the numbers, starting from the one’s place.
- For finding the difference between two or more fractions, we convert each function into an equivalent fraction having the same denominator. This is done by finding the Least Common Multiple ( L.C.M) of the denominators. Then we subtract their numerators.
- For finding the difference between two or more decimal numbers, write down the decimal numbers, one number under the other number and line up the decimal points. Convert the given decimals to like decimals. Arrange the addends in such a way that the digits of the same place are in the same column. Subtract the numbers from the right as we carry addition usually.









