Position and Direction

Introduction

Students compare amounts and objects using everyday language to discuss size, weight, capacity, position, distance, time, and money. They identify, make, and characterize patterns. Students look at commonplace features of shapes and objects and describe them using mathematical terms. The students’ skills to do these tasks involve understanding position and direction. 

We’ll discuss location and direction in this article, the characteristics of everyday objects and shapes and how to describe them using mathematical terminology.

What is a position?

Definition

The placement of an object is its position. It is the ability to describe how one object relates to another.

What is a direction?

Definition

A direction is an information that tells how or in what order to do something. It is the act of guiding or choosing a way to proceed.

Positional Language 

The terms and phrases used to describe a person or an object’s position are known as positional words (or language). Positional word comprehension takes some time. Most kids require some time first to understand the terms and then more time to begin using the phrases themselves. Some examples of positional words, “in”, “on”, “over”, “under”, “behind”, “next to”, “in front of”.

Here are some examples of sentences with positional words using the image below.

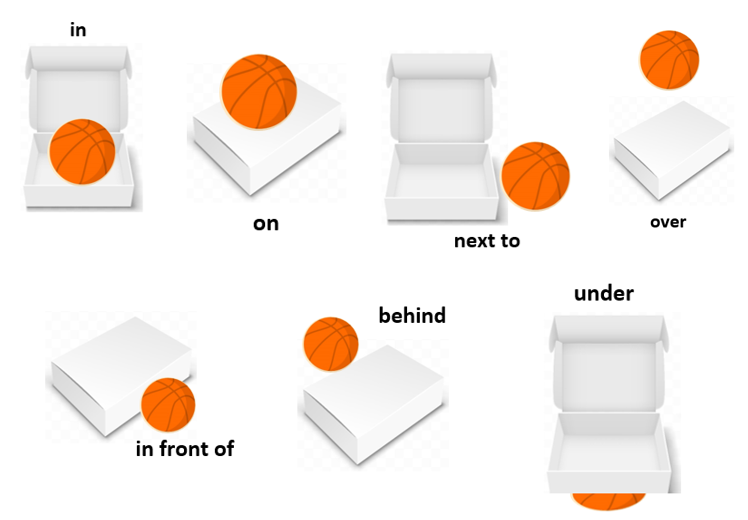
1. The ball is in the box.

2. The ball is on the box.

3. Next to the box is a ball.

4. The ball is over the box.

5. A ball is in front of a box.

6. The ball is behind the box.

7. A ball is under the box.

Positions in Races or Queues 

A number that denotes the position or order of something in relation to other numbers is known as an ordinal number. For example, first (1^st ), second (2^nd ), third (3^rd ), fourth (4^th ), and so on.

Positions in Races

Let us say, for instance, six boys are racing to the finish line. Assuming they cross the finish line as shown in the picture below, let’s use ordinal numbers to show their positions.

Anton finished the race in 1^st place.
Jo finished the race in 2^nd place.
Zack finished the race in 3^rd place.
Nathaniel finished the race in 4^th place.
Michael finished the race in 5^th place.
Ashley finished the race in 6^th place.

Positions in Queues

In the illustration below, we have a queue of students buying cotton candy. Look carefully and answer the questions below.

1. Who is first in the queue?
2. Who is last in the queue?
3. Who is between Maggie and Rose?
4. Who is between Jim and Billy?
5. Who is between Catherine and Rose?
6. Who is between Billy and Kevin?

Answers:

1. Jim is first in the queue to buy cotton candy.
2. Catherine is last in the queue to buy cotton candy.
3. Kevin is between Maggie and Rose.
4. Amy is between Jim and Billy.
5. Martin is between Catherine and Rose.
6. Maggie is in between Billy and Kevin.

If we are going to order this queue of students buying cotton candy from first (1^st ) place to tenth (10^th ) place, we have,

1^st place – Jim
2^nd place – Amy
3^rd place – Billy
4^th place – Maggie
5^th place – Kevin
6^th place – Rose
7^th place – Martin
8^th place –  Catherine

Left and Right Positions

The hands below show us which way is left and which is right.

There is a trick of remembering your left from your right. Your left-hand makes an “L shape”. L for left. 

Now let us look at the queue of shapes below and let us look at their position from the left and from the right.

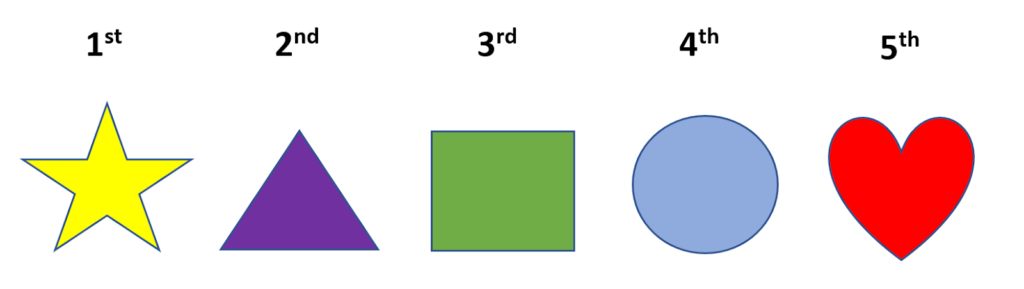
Looking at the position of the shapes from the left, we have,

The star is first (1^st) from the left. 

The triangle  is second (2^nd )  from the left.

The square is third (3^rd ) from the left.

The circle is fourth (4^th ) from the left. 

The heart is fifth (5^th ) from the left.

We can also say that the heart is last from the left.

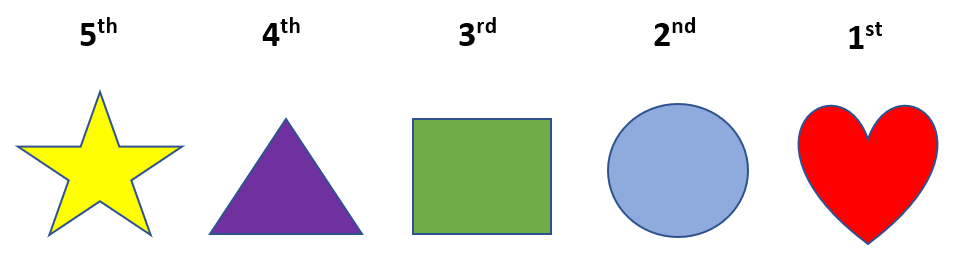
Looking at the position of the shapes from the right, we have,

The heart is first (1^st) from the left. 

The circle is second (2^nd )  from the left.

The square is third (3^rd ) from the left.

The triangle is fourth (4^th ) from the left. 

The star is fifth (5^th ) from the left.

We can also say that the star is last from the left.

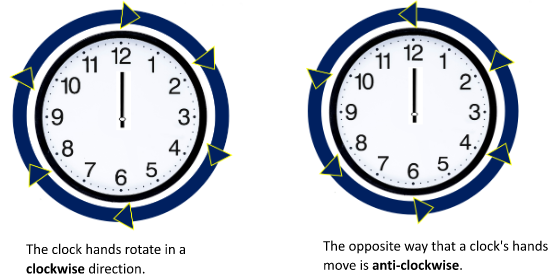
Linking Turns with the Hands on a Clock

Clockwise involves turning to the right as it moves in the same direction as the hands of a clock, whereas anti-clockwise requires turning to the left in opposition to the direction of a clock’s hands.

The arrows below indicate the movement of clockwise and anti-clockwise rotation.

Making Turns in Both Directions

Let us have the circle below and divide it into four equal parts.

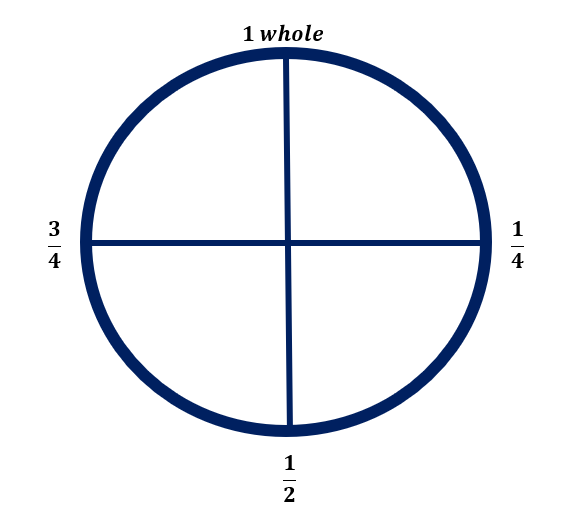
We have learned in fractions that when we divide a shape into four equal parts, each part is called a quarter. When we join two quarters, we get half. When we join three, then we get three quarters. And when we join four quarters, we get one whole.

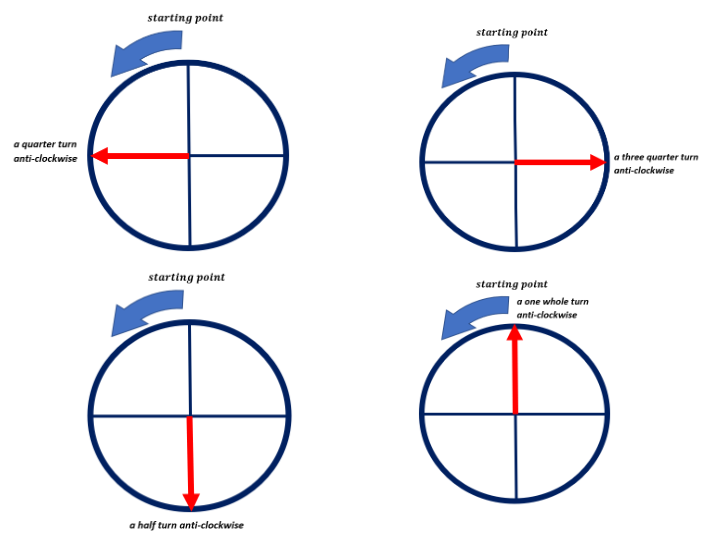
The following shows a quarter clockwise, a half turn clockwise, a quarter turn clockwise, and one whole turn clockwise. Notice the position of the starting point and the direction of the red arrow where an object should be facing. Turning a quarter makes 90 degrees, half makes 180 degrees, turning ¾ makes 270 degrees, and a full rotation makes 360 degrees.  

The images below show a quarter turn anti-clockwise, a half turn anti-clockwise, a three-quarter turn anti-clockwise, and a whole turn anti-clockwise.

Compass Directions

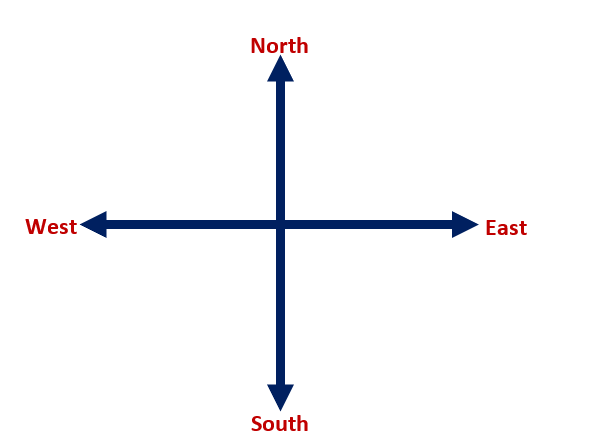
For the compass directions, we have the North, East, South, and West. So, this is starting from the north and working clockwise is East, then South, and then West. These directions are also known as cardinal directions.

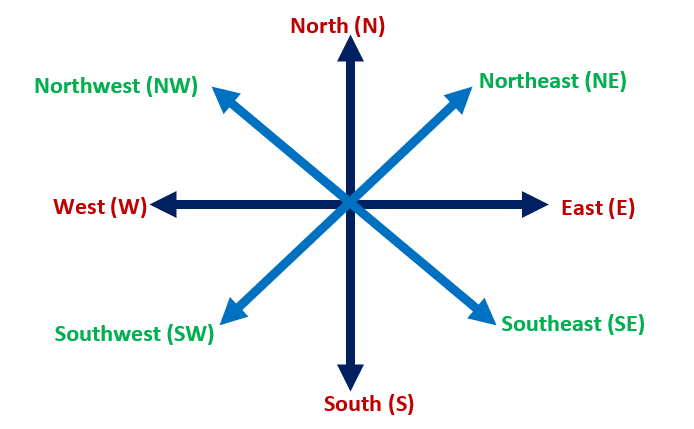
There are also directions that are in between the four major directions above. The direction between north and east is known as northeast. The direction between south and east is known as the southeast. The direction between south and west is known as southwest. And the direction between north and west is known as northwest. They are also called intermediate directions.

Let us say we are asked to refer to the letters below and use the cardinal or intermediate direction.

K	A	M
P	B	G
R	S	T

Questions:

1. What is the direction from the letter B to A? 
2. What is the direction from the letter B to G?
3. What is the direction from the letter B to P?
4. What is the direction from the letter B to S?
5. What is the direction from the letter B to T?
6. What is the direction from the letter B to K?
7. What is the direction from the letter B to R?
8. What is the direction from the letter B to M?

Solution:

Since the letter B is located at the centre of the image, the direction of other surrounding letters from it can be easily identified using the cardinal and intermediate directions.

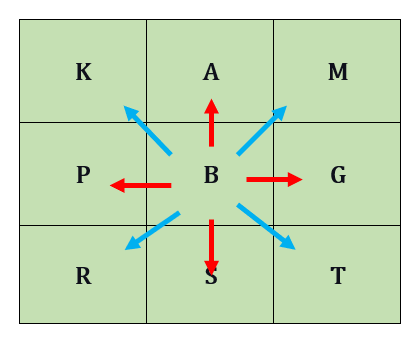
For questions 1 to 4,

1. A is north of B.
2. G is east of B.
3. P is west of B.
4. S is south of B.

For questions 5 to 8,

5. T is southeast of B.
6. K is northwest of B.
7. R is southwest of B.
8. M is northeast of B.

Follow-up questions:

Which letter is north of the letter T? Answer: G
Which letter is southeast of the letter P? Answer: S
Which letter is southwest of letter M? Answer: B
Which letter is northwest of G? Answer: A

Position on a 2-D grid

Grid Location

A grid is a pattern of intersecting horizontal and vertical lines that forms a collection of squares.

For example, if we have the grid below, we are asked to identify the location of the objects in it.

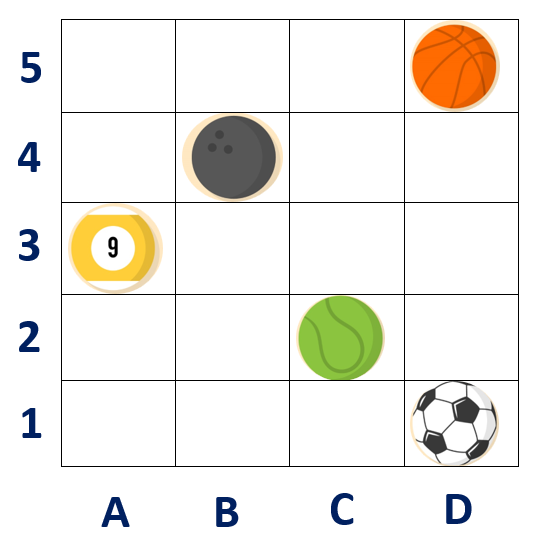
In the given grid, we have different balls in different positions. The grid has squares forming four columns using the letters A, B, C, and D, and five rows using the numbers 1, 2, 3, 4 and 5.

The billiard ball is in the A3 position since it is in column A and row 3.

The bowling ball   is in the B4 position since it is in column B and row 4.

The tennis ball   is in the C2 position since it is in column C and row 2.

The basketball    is in the D5 position since it is in column D and row 5.

The soccer ball    is in the D1 position since it is in column D and row 1.

Coordinate Plane

The intersection of two number lines creates a two-dimensional plane known as a coordinate plane. The x-axis, one of these number lines, is a horizontal number line, and the y-axis, another number line, is vertical. Four quadrants—Quadrant I, Quadrant II, Quadrant III, and Quadrant IV—make up the coordinate plane. The origin (0,0) is the intersection of these lines. The coordinate plane that is formed by these two number lines’ perpendicular intersections looks like this:

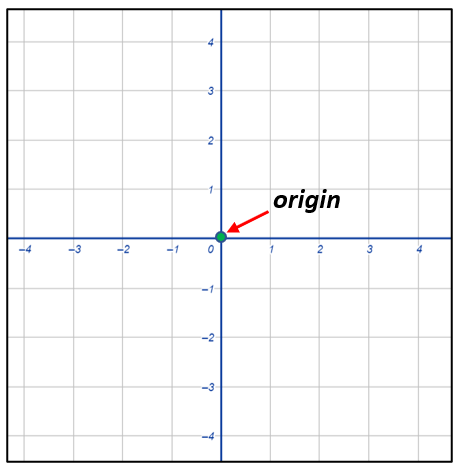
Every coordinate plane point is expressed as an ordered pair (x,y), where x and y are numbers that represent the point’s position in relation to the x- and y-axes, respectively. 

Let us say, for example, that we want to describe the positions of the points A, B, C, and D in the illustration below with respect to the x- and y- axis, respectively.

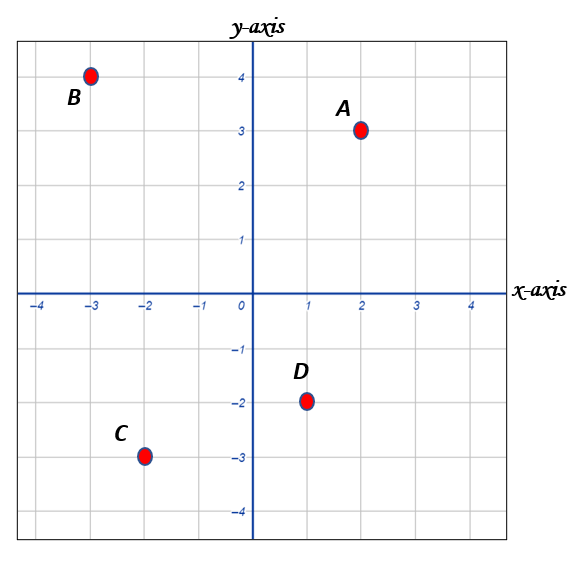
The position of point A on the x-axis is 2 units and, on the y- axis is 3 units. Thus, we have the position of point A as A ( 2, 3 ).

Since the position of point B on the x-axis is -3 units and on the y- axis is 4 units, then the ordered pair of point B is ( -3, 4 ).

Point C is located 3 units down the x-axis, and 2 units left the y-axis. As a result, we have point C’s location ( -2, -3 ).

Point D is at a location of 1 unit on the x-axis and -2 units on the y-axis; hence its ordered pair is ( 1, -2 ).

More Examples

Example 1

Look at the objects below and identify how they have moved by answering a quarter turn, a half turn, a three-quarter turn, or a whole turn. (suppose that the given objects all moved)

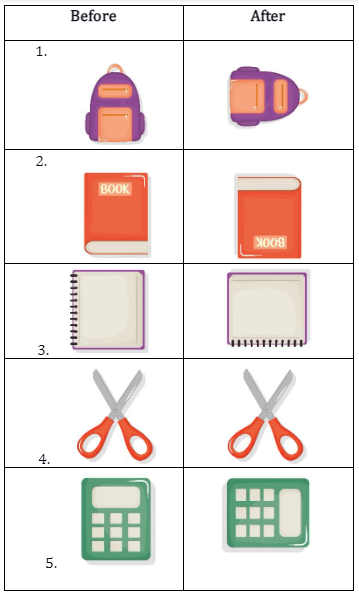
Answers:

1. The bag moved a quarter turn.
2. The book moved a half turn.
3. The notebook moved a three-quarter turn.
4. The scissor moved a whole turn.
5. The calculator moved a quarter turn.

Example 2

Use the correct positional word to complete the sentence.

Choices: above, in, under, left, right, in, on, between

1. The notebook is _____ the box.
2. The pencil is in _______ the sharpener and the calculator.
3. The color pencils are ____ the pencil.
4. The bag is ____ of the color pencils.
5. The calculator is ____ of the pencil.
6. The book is _____ the pencil.
7. The bag is ______ the sharpener.

Answers:  

1. The notebook is in the box.
2. The pencil is in between the sharpener and the calculator.
3. The color pencils are above the pencil.
4. The bag is left of the color pencils.
5. The calculator is right of the pencil.
6. The book is under the pencil.
7. The bag is above the sharpener.

Example 3:

Find the position of the school bus in the grid and suppose it will move following the directions stated in each number. Use position A1 as the starting point of the school bus.

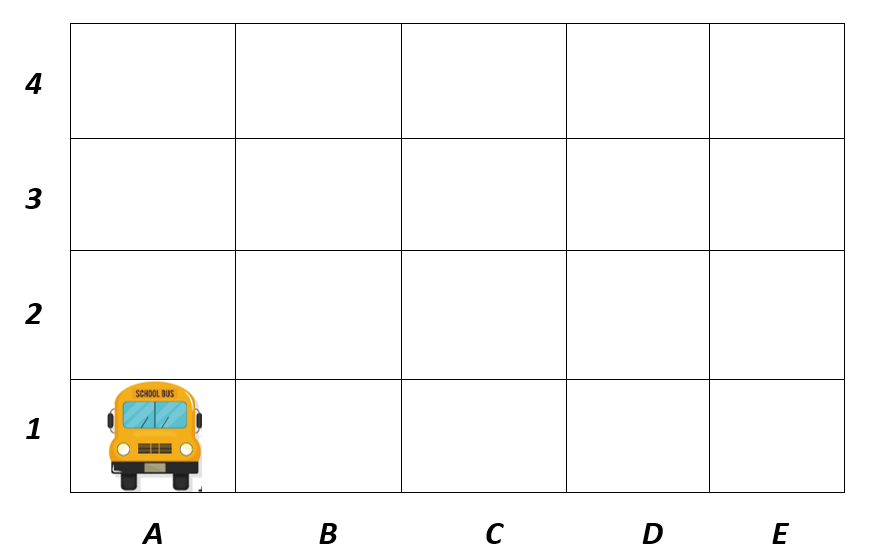
1. up, right,  down, right, right, up
2. right, up, up, up, right, right, down
3. up, up, right, down, right, right, up, right
4. right, right, up, left, left, up, up
5. up, down, right, right, up, up, left, up, right, down
6. right, up, right, up, right, up, right
7. up, right, up, left, up, right, right, down, right, down, left

Answers:

1. The school bus will be at position D2.
2. The school bus will be at position D3.
3. The school bus will be at position E3.
4. The school bus will be at position A4.
5. The school bus will be at position C3.
6. The school bus will be at position E4.
7. The school bus will be at position C2.

Example 4:

Use the grid below to answer the questions:

1. Which shape is at position C4?
2. Which shape is at position A4?
3. Which shape is at position B2?
4. Which shape is at position D1?

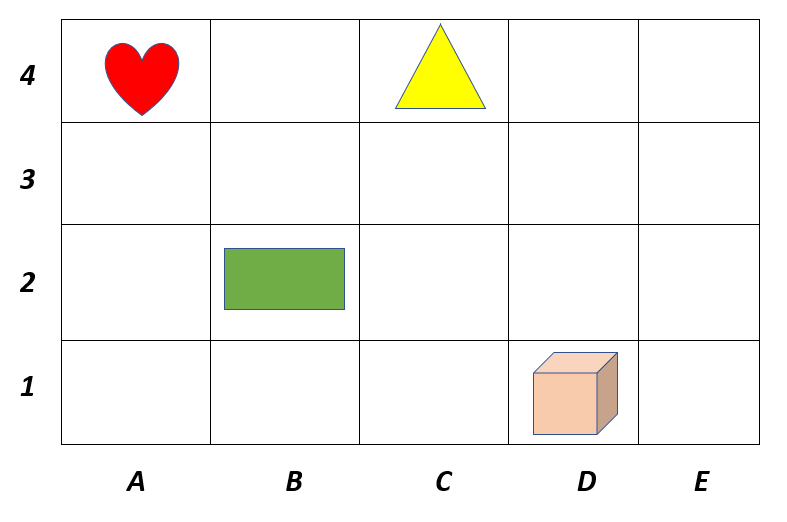
Answers:

1. The triangle is at position C4.
2. The heart is at position A4.
3. The rectangle is at position B2.
4. The cube  is at position D1.

Example 5:

Refer to the map below to answer the questions.

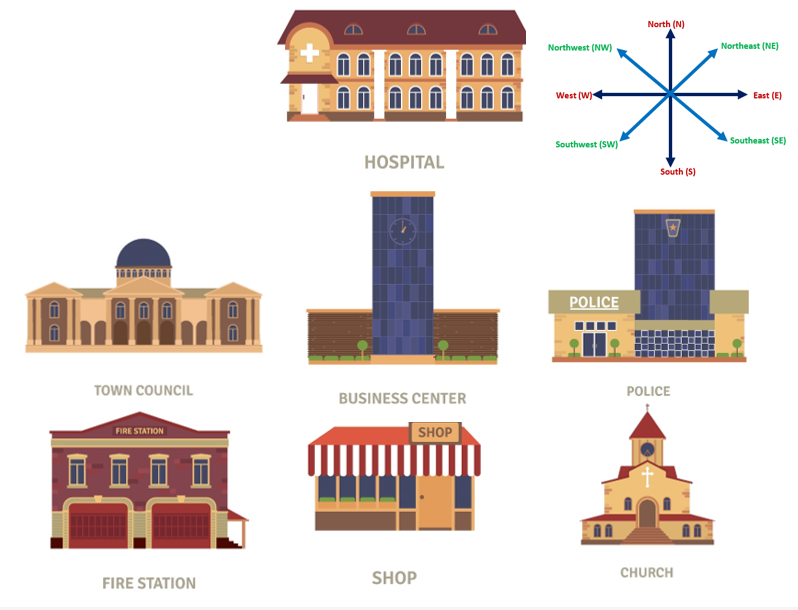
Questions:

1. Which is north of the business center?
2. Which is south of the police station?
3. Which is east of the town council?
4. Which is west of the church?
5. Which direction is the business center from the church?
6. Which direction is the police station from the shop?
7. Which direction is the fire station from the business center?
8. Which direction is the town council from the hospital?

Answer:

1. The hospital is north of the business center.
2. The church is south of the police station.
3. The business center is east of the town council.
4. The shop is west of the church.
5. The business center is northwest of the church.
6. The police station is northeast of the shop.
7. The fire station is southwest of the business center.
8. The town council is southwest of the hospital.

Example 6:

Points A, B, C and D form a rectangle. These are the coordinates of points B, C, and D. 

B (-3, -2) , C ( 3, -2 ), and D ( 3, 2 ). Find the position of point A.

Solution:

The image below shows the position of the four points that make up the triangle. Point A must be at ( -3, 2).

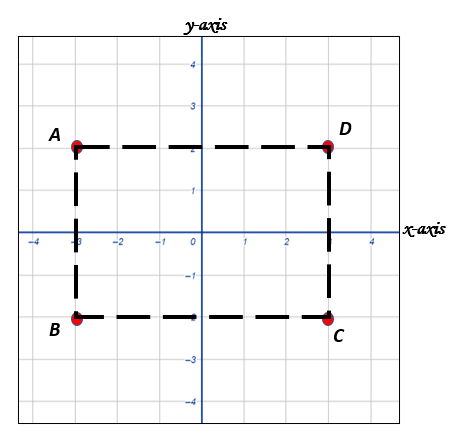
In answering this type of question, we must be mindful of the lengths of the sides of the rectangle. We must ensure that it has two pairs of parallel sides, and these sides must have equal lengths. In this example, side AB is parallel with side DC, and both sides measure 4 units. Side AD and side BC are parallel, and both measures 6 units.

Summary

Position

The placement of an object is its position. It is the ability to describe how one object relates to another.

Direction

A direction is an information that tells how or in what order to do something. It is the act of guiding or choosing a way to proceed.

Terms and phrases used to describe a person or an object’s position are known as positional words (or positional language). Some examples of positional words, “in”, “on”, “over”, “under”, “behind”, “next to”, “in front of”.

A number that denotes the position or order of something in relation to other numbers is known as an ordinal number. For example, first (1^st ), second (2^nd ), third (3^rd ), fourth (4^th ), and so on.

The arrows below show us which way is left and which is right.

Clockwise involves turning to the right as it moves in the same direction as the hands of a clock. 

Anti-clockwise requires turning to the left in opposition to the direction of a clock’s hands.

Turning a quarter makes 90 degrees, half makes 180 degrees, turning ¾ makes 270 degrees, and a full rotation makes 360 degrees.  

West, north, east, and south are the four cardinal directions.

The intermediate directions are northeast, northwest, southeast, and southwest.

A grid is a pattern of intersecting horizontal and vertical lines that forms a collection of squares.

The intersection of two number lines creates a two-dimensional plane known as a coordinate plane.

The origin ( 0, 0 ) is the point at which the x- and y-axes intersect.

Frequently Asked Questions (FAQs)

What is the difference between position and direction?

The placement of an object is its position. It is the ability to describe how one object relates to another, while direction is information that tells how or in what order to do something.

What are positional words?

Terms and phrases used to describe a person or an object’s position are known as positional words (or positional language). 

What are examples of positional words?

Some examples of positional words are, “in”, “on”, “over”, “under”, “behind”, “next to”, “in front of”, “below”, “above”, “over”, etc.

What are directions used for?

To understand where something is in relation to another, consider its direction. The term “direction” is more precise when used geographically. Direction can also refer to a specific location. Let us say, for example, how will you go to school from home. Direction can also represent movement.

What is the difference between clockwise and anti-clockwise?

Clockwise involves turning to the right as it moves in the same direction as the hands of a clock, whereas anti-clockwise requires turning to the left in opposition to the direction of a clock’s hands.

What are quarter turn and half turn?

A quarter turn makes 90 degrees; a half turn makes 180 degrees, a three-quarter turn makes 270 degrees, and a whole turn makes 360 degrees.

How many quarter turns makes a half turn?

Two quarter turns to make a half turn.

What is the difference between cardinal and intermediate directions?

These are the four cardinal directions: south, east, north, and west.

The intermediate directions are northeast, northwest, southeast, and southwest.

Why is it important to teach students position and direction?

Teaching position and direction is important for the students to understand places; positional words must be used. As a student develops his independence and ability to complete tasks, he becomes aware of how important information like object placement is. For instance, you can ask a student to move some stuff inside the room or get something from the faculty room. To complete the task correctly, they should be able to understand their position and follow directions.

Recommended Worksheets

Directions (National Aviation Day Themed) Math Worksheets
Describing Objects and its Relative Position Kindergarten Math Worksheets
Cartesian Coordinate Plane (Adventure Themed) Worksheets