Definition
Cartesian product is the product of any two sets, in an ordered form. This means that the resultant set of the Cartesian product of two sets contains all possible and ordered pairs such that the first element of the pair belongs to the first set and the second element belongs to the second set.
Let us recall what we mean by ordered pair.
An ordered pair consists of two objects or elements in a given fixed order. Let us understand it through an example. Suppose we have A and b as two sets. Then by ordered pair of elements we mean a pair ( a , b ) in that order, where a ∈ A and b ∈ B. it is important to note here that an ordered pair is not a set consisting of two elements. The ordering of the two elements in an ordered pair is important and the two elements need not be distinct. Now let us learn about the Cartesian product of sets.
How to Find Cartesian product
Let A and B be two non-empty sets. The set of all ordered pairs ( a , b ) such that a A and b B is called the Cartesian product of the sets A and B and is denoted by A x B. Thus,
A x B = { ( a , b ) : a ∈ A and b ∈ B }
Let us understand it through an example.
Suppose we have two sets, A = { 2 , 4 , 6 } and B = { 1 , 2 }, then what would be the value of A x B?
We will have,
A x B = { 2 , 4 , 6 } x { 1 , 2 } = { ( 2 , 1 ) , ( 2 , 2 ) , ( 4 , 1 ) , ( 4, 2 ) , ( 6 , 1 ) , ( 6 , 2 )
What would be the value of B X A?
B x A = { 1 , 2 } x ( 2 , 4 , 6 } = { ( 1 , 2 ) , ( 1 , 4 ) , ( 1 , 6 ) , ( 2 , 2 ) , ( 2 , 4 ) , ( 2 , 6 ) }
It can be seen from the above example that to write A x B we take an element from set a and form all ordered pairs with this element as the first element and elements of B as second elements. Next, we choose another element from A and corresponding to each element in B we form ordered pairs with this element as the first element and elements of B as the second element. This process is continued till all elements of A are exhausted.
Let us consider another example.
Example If A = { a , b } and B = { 1 , 2 , 3 }, find A x B, B x A, A x A, B x B and ( A x B ) ∩ ( B x A )
Solution We have been given the sets, A = { a , b } and B = { 1 , 2 , 3 }. We need to find A x B, B x A, A x A, B x B and ( A x B ) ∩ ( B x A ).
Let us find them one by one.
We have, A = { a , b } and B = { 1 , 2 , 3 }, therefore,
A x B = { a , b } x { 1 , 2 , 3 } = { ( a , 1 ) , ( a , 2 ) , ( a , 3 ) , ( b , 1 ) , ( b , 2 ) , ( b , 3 ) }
Hence, A x B = { ( a , 1 ) , ( a , 2 ) , ( a , 3 ) , ( b , 1 ) , ( b , 2 ) , ( b , 3 ) } . . . . . . . . . . ( 1 )
B x A = { 1 , 2 , 3 } x { a , b } = { ( 1 , a ) , ( 1 , b ) , ( 2 , a ) , ( 2 , b ) , ( 3 , a ) , ( 3 , b ) }
Hence, B x A = { ( 1 , a ) , ( 1 , b ) , ( 2 , a ) , ( 2 , b ) , ( 3 , a ) , ( 3 , b ) } . . . . . . . . ( 2 )
A x A = { a , b } x { a , b } = { ( a , a ) , ( a , b ) , ( b , a ) , ( b , b ) }
Hence, A x A = { ( a , a ) , ( a , b ) , ( b , a ) , ( b , b ) } . . . . . . . . . . . . . . . . . . . ( 3 )
B x B = { 1 , 2 , 3 } x { 1 , 2 , 3 } = { ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 2 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 1 ) , ( 3 , 2 ) , ( 3 , 3 ) }
Hence, B x B = { ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 2 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 1 ) , ( 3 , 2 ) , ( 3 , 3 ) } . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 4 )
Now, to find the value of ( A x B ) ∩ ( B x A ), from ( 1 ) and ( 2 ) we have,
A x B = { ( a , 1 ) , ( a , 2 ) , ( a , 3 ) , ( b , 1 ) , ( b , 2 ) , ( b , 3 ) } and
B x A = { ( 1 , a ) , ( 1 , b ) , ( 2 , a ) , ( 2 , b ) , ( 3 , a ) , ( 3 , b ) }
We can see above that A x B and B x A have no elements in common. Hence, ( A x B ) ∩ ( B x A ) = ∅
Properties of Cartesian product
The following are the properties of Cartesian product –
- Cartesian product does not satisfy commutative law, i.e. it is not commutative. This means that if we change the order of sets the result also changes. For instance, if A and B are two sets, then the Cartesian product of A and B, A × B ≠ B × A.
- Cartesian product does not satisfy associative law, i.e. is not associative. This means that if we regroup the sets in the Cartesian product, then it will change the result. For instance, if A, B and C are three sets, then ( A × B ) × C ≠ A × ( B × C )
- Distribution property of Cartesian product over the intersection of sets is given by A × (B ∩ C) = ( A × B ) ∩ ( A × C )
- Distribution property of Cartesian product over the union of sets is given by A × ( B ∪ C ) = ( A × B ) ∪ ( A × C )
- The result of the Cartesian product of sets is a set of all ordered pairs.
Cartesian product of more than two Sets
Let A, B and C be three sets. Then, A x B X C is the set of all ordered triplets having the first element of A, second element from B and third element from C. This can be stated as –
A x B x C = { ( a , b ,c ) : a ∈ A , b ∈ B , c C }
Let us understand it through an example.
Suppose we have three sets, A = { 1 , 2 } , B = { 3 , 4 } and C = { 4 , 5 , 6 } , then
A x B = { 1 , 2 } x { 3 , 4 } = { ( 1 , 3 ) , ( 1 , 4 ) , ( 2 , 3 ) , ( 2 , 4 )
Now,
A x B x C = ( A x B ) x C = { ( 1 , 3 ) , ( 1 , 4 ) , ( 2 , 3 ) , ( 2 , 4 ) x { 4 , 5 , 6 } This means that
A x B x C = { ( 1 , 3 , 4 ) , ( 1 , 3 , 5 ) , ( 1 , 3 , 6 ) , ( 1 , 4 , 4 ) , ( 1 , 4 , 5 ) ( 1 , 4 , 6 ) , ( 2 , 3 , 4 ) ( 2 , 3 , 5 ) , ( 2 , 3 , 6 ) , ( 2 , 4 , 4 ) ( 2 , 4 , 5 ) , ( 2 , 4 , 6 ) }
It is important to note here that A x B x C = ( A x B ) x C = A x ( B x C )
Number of elements in the Cartesian product of Sets
Can we determine the number of elements that should be present in the Cartesian product of two sets? If A and B are two finite sets then n ( A x B ) = n ( A ) x n ( B ). This means that if a set A has m elements while a set B has n elements then, the number of elements of A x B would be m n.
Graphical representation of Cartesian Product of Sets
Let A and B be two non-empty sets. To represent A x B graphically, we draw two mutually perpendicular lines, one horizontal and one vertical. On the horizontal line we represent the elements of set A while on the vertical line we represent the elements of set B. If a A and b B, we draw a vertical through a and a horizontal line through B. these two lines will meet in a point which will denote the ordered pair ( a , b ). In this manner we mark points corresponding to each ordered pair in A x B. let us understand it through an example.
Suppose we have two sets, A = ( a , b , c } and B = { 1 , 2 }
Then, A x B = { ( a , 1 ) , ( a , 2 ) , ( b , 1 ) , ( b , 2 ) , ( c , 1 ) , ( c , 2 ) }
The graphical representation of the above Cartesian product will be –
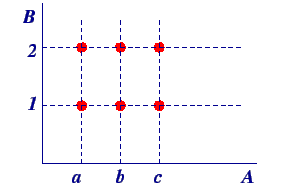
Diagrammatic Representation of Cartesian product of Two Sets
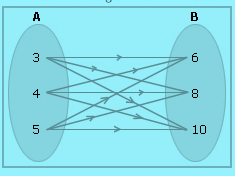
In order to represent A x B by an arrow diagram, we first draw Venn diagrams representing sets A and B one opposite to the other. Next, we draw line segments starting from each element of A and terminating to each element of set B.
Let us understand it through an example.
Suppose we, have two sets, A = { 3 , 4 , 5 } and B = { 6 , 8 , 10 }
Now, A x B = { ( 3 , 6 ) , ( 3 , 8 ) , ( 3 , 10 ) , ( 4 , 6 ) , ( 4 , 8 ) , ( 4 , 10 ) , ( 5 , 6 ) , ( 5 , 8 ) , ( 5 , 10 )
We can see that n ( A ) = 3 , n ( B ) = 3 and n ( A x B ) = 3 x 3 = 9
The above Cartesian product can be represented using the arrow diagram as shown below –
Key Facts and Summary
- Cartesian product is the product of any two sets, in an ordered form.
- An ordered pair consists of two objects or elements in a given fixed order.
- Let A and B be two non-empty sets. The set of all ordered pairs ( a , b ) such that a A and b B is called the Cartesian product of the sets A and B and is denoted by A x B. Thus, A x B = { ( a , b ) : a ∈ A and b ∈ B }
- Let A, B and C be three sets. Then, A x B X C is the set of all ordered triplets having the first element of A, the second element from B and the third element from C.
- The cartesian product does not satisfy commutative law, i.e. it is not commutative. This means that if we change the order of sets the result also changes. For instance, if A and B are two sets, then the Cartesian product of A and B, A × B ≠ B × A.
- The cartesian product does not satisfy associative law, i.e. is not associative. This means that if we regroup the sets in the Cartesian product, then it will change the result. For instance, if A, B and C are three sets, then ( A × B ) × C ≠ A × ( B × C )
- The distribution property of the Cartesian product over the intersection of sets is given by A × (B ∩ C) = ( A × B ) ∩ ( A × C )
- The distribution property of the Cartesian product over the union of sets is given by A × ( B ∪ C ) = ( A × B ) ∪ ( A × C )
- The result of the Cartesian product of sets is a set of all ordered pairs.
- If A and B are two finite sets then n ( A x B ) = n ( A ) x n ( B ). This means that if a set A has m elements while a set B has n elements then, the number of elements of A x B would be m n.
Recommended Worksheets
Cartesian Coordinate Plane (Adventure Themed) Worksheets
Number Lines and Coordinate Planes 6th Grade Math Worksheets
Graphing Points on the Coordinate Plane 5th Grade Math Worksheets









