Function Transformations

Introduction

The concept of function is of paramount importance in mathematics and among other disciplines as well. Functions form one of the most important building blocks of Mathematics. The word function has been derived from the Latin word meaning operation and the words mapping and map are synonymous with it. Functions play an important role in differential and integral calculus.

Let A and B be two non-empty sets. A relation f from A to B, i.e. a subset of A x B is called a function or a mapping or a map from A to B is,

1. For each a ∈ A there exists b ∈ B such that ( a, b ) ∈ f
2. ( a, b ) ∈ f and ( a, c ) ∈ f ⇒ b = c

Thus a non-void set f of A x B is a function from A to B if each element of A appears in some ordered pair in f and no two ordered pairs in f have the same first element.

If ( a, b ) ∈ f, then b is called the image of a under f.

Domain, Co-domain and Range of a Function

Let f : A → B. then the set A is known as the domain of f and the set B is known as the range co-domain of f. The set of all f-images of elements of A is known as the range of f or image set of A under f and is denoted by f ( A ).

Thus f ( A ) = { f (x)  : x ∈ A } = Range of f

Definition

What do we mean by the word “transform”? To transform means to change from one form to another. So, by that definition, transformation of a function means to change it from one from to another. Hence, transformations of functions mean transforming the function from one form to another.

We can thus say that function transformations are mathematical operations that cause change in the shape of a graph. When a graph of a function is changed in appearance or location, we call it a transformation.

Let us understand it by an example.

Graph

Look at the graph f ( x ) =  x² + 3. The graph of this function will be shown below –

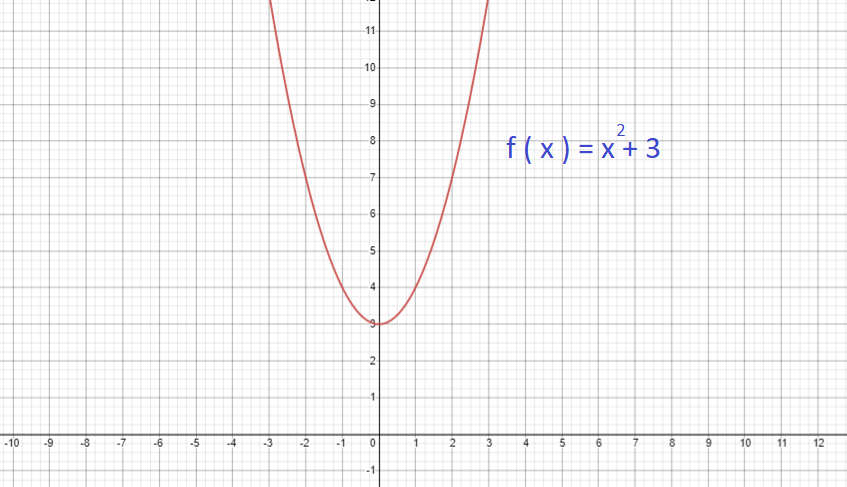
We can clearly see that the graph is 3 units above the quadratic equation f (  x ) =  x²

We can visualise the transformation by plotting both the graphs on the same plane.

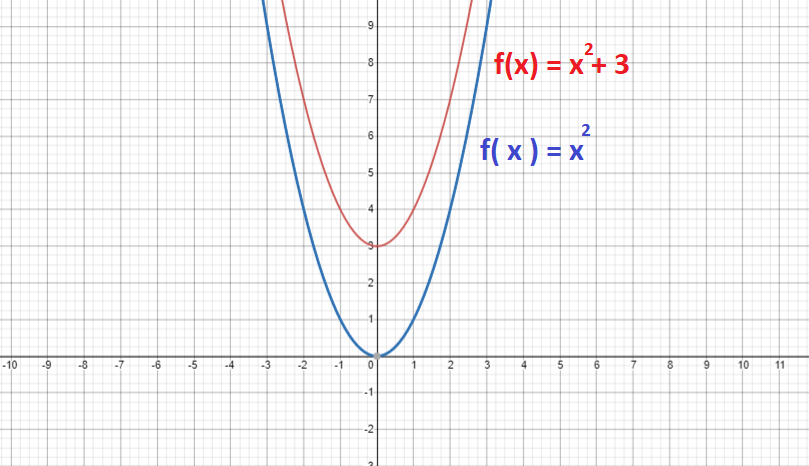
In how many can we transform the functions? Let us find out.

Types of Transformations

There are four major types of transformations of functions. they are – 

1. Translation
2. Rotation
3. Reflection
4. Dilation

Let us discuss them one by one.

Transformation of Functions using Translation

Translation transformation slides or moves the object in the space by keeping its size and orientation the same. It is important to note here that, a translation moves every point by a fixed distance in the same direction. The movement is caused by the addition or subtraction of a constant from a function. Translation transformation slides or moves the object in the space by keeping its size and orientation the same.  Let us understand it by an example.

Suppose we have a function, f ( x ) = x² – 1

The graph of this function will be – 

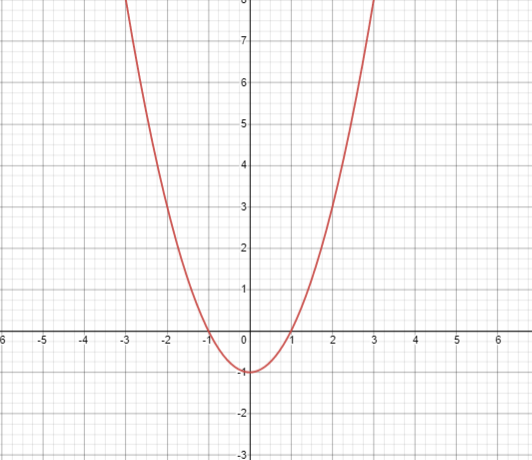
Now, if we want to translate this graph by f ( x ) = f ( x ) + 1, what will we do?

We will have,

f ( x ) = f ( x ) + 1

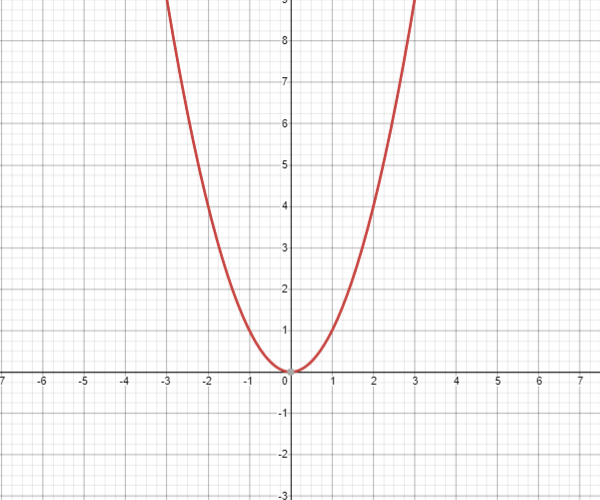
⇒ f ( x ) = x² – 1 + 1 

⇒ f ( x ) = x²

So, the graph of the function will now become,

Transformation of Functions using Rotation

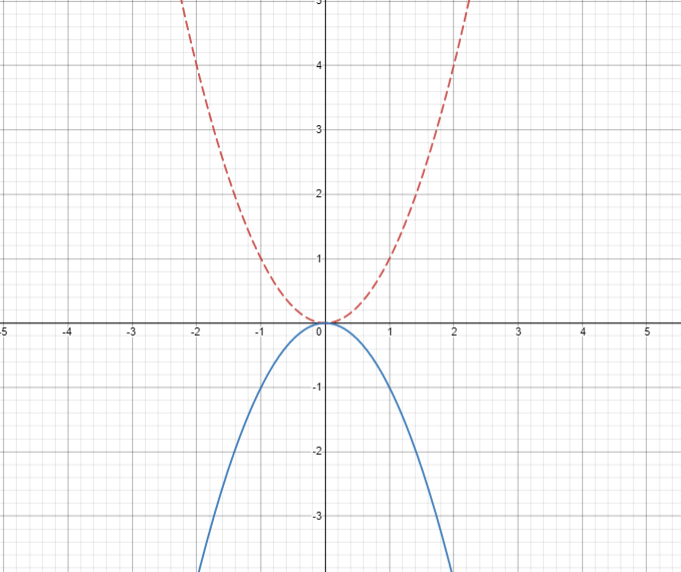
A rotation is a transformation that is performed by “spinning” the object around a fixed point known as the centre of rotation. In other words, Rotation Transformation rotates or turns the curve around an axis without changing the size and shape of an object. Let us understand it by an example.

Suppose we have a function f ( x ) = x ²

The graph of this function will be – 

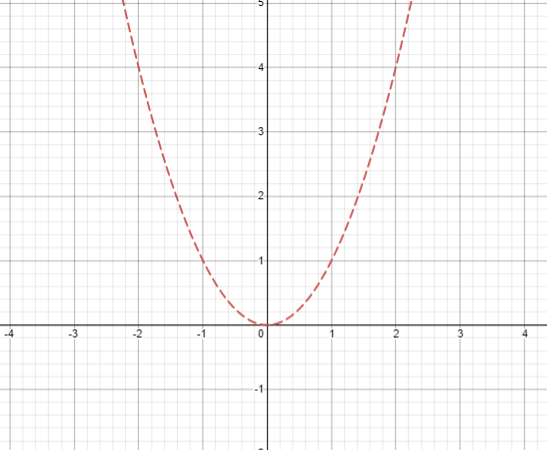
Now, suppose we rotate this function at an angle of 180o. What would be the function be like now? The following graph demonstrates the original function as well as the function obtained after rotation.

Transformation of Functions using Reflection

A reflection of a function causes the graph to appear as a mirror image of the original function. In other words, switching the sign of the input going into the function leads to the reflection of the function. This also means that Reflection Transformation flips the object across a line by keeping it size or shape constant. Let us understand it by an example.

Suppose we have a function f ( x ) = x ⁵

The graph of this function will be – 

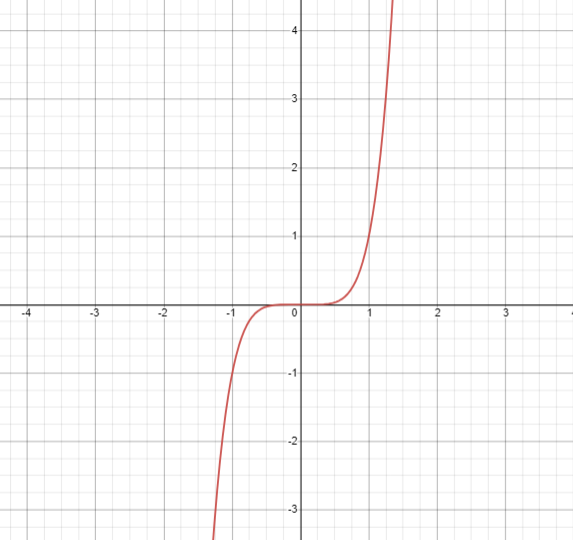
Now, if we were to fin the reflection of this function, it would be given by 

f ( x) =  – f ( x )

This means that the reflection of the function f ( x ) = x ⁵ will be f ( x ) = – x ⁵

The following graph demonstrates the original function as well as the function obtained after reflection

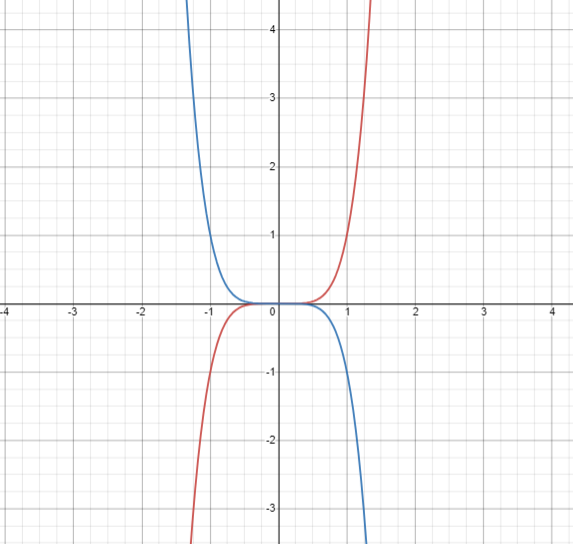
Transformation of Functions using Dilation

Dilation or scaling is a transformation that changes the size and/or the shape of the graph of the function. It is important to note here that this is the only manner in which we can change the size of the function. In none of the transformations we discussed could change the size and shape of a function. Dilation transformation enlarges or shortens the object by keeping its shape or orientation the same. This is known as resizing.

Let us understand it by an example.

Suppose we have a function f ( x ) = x ³

The graph of this function will be – 

Now, if we multiply the function by 2, we will have, 2 f ( x ) = 2 x ³

This means that every point on the graph of the original function gets multiplied by two. The demonstrates the original function as well as the function obtained after dilation –

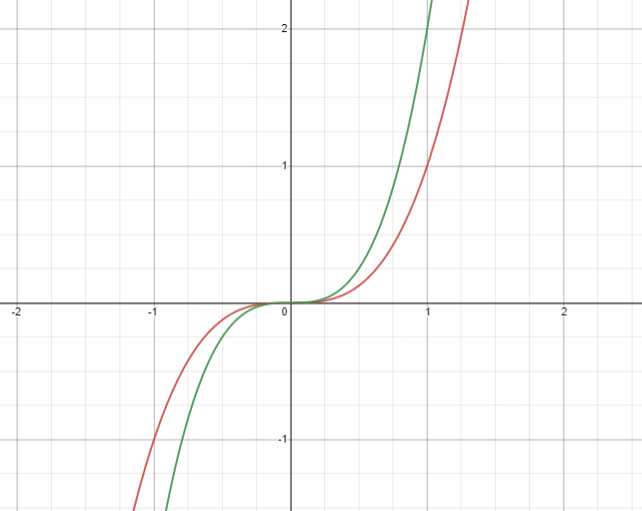
Rules

The following are the rules for function transformations – 

1. For transformation of f ( x ) to f ( x ) + a, f ( x) is shifted upwards by a units. For example, if we have a function, f ( x ) = x² + x and we want to move it 3 points up, the transformation of f ( x ) will be 

f ( x ) → f ( x ) + 3

⇒ f ( x ) =  x² + x + 3

So, if we have a point ( x , y ) on the function f ( x ), it will now be transformed to (x, y + 3 ).

2. For transformation of f ( x ) to f ( x ) – a, f ( x) is shifted downwards by a units. For example, if we have a function, f ( x ) = x² + x and we want to move it 3 points down, the transformation of f ( x ) will be 

f ( x ) → f ( x ) – 3

⇒ f ( x ) =  x² + x – 3

So, if we have a point ( x , y ) on the function f ( x ), it will now be transformed to (x, y – 3 ).

3. For transformation of f ( x ) to f ( x + a ) , f ( x) is shifted left by a units. For example, if we have a function, f ( x ) = x² + x and we want to move it 3 points left, the transformation of f ( x ) will be 

f ( x ) → f ( x + 3 ) 

⇒ f ( x ) =  ( x + 3 ) ² + ( x + 3 ) 

So, if we have a point ( x , y ) on the function f ( x ), it will now be transformed to (x – 3, y ).

4. For transformation of f ( x ) to f ( x – a ) , f ( x) is shifted right by a units. For example, if we have a function, f ( x ) = x² + x and we want to move it 3 points right, the transformation of f ( x ) will be 

f ( x ) → f ( x – 3 ) 

⇒ f ( x ) =  ( x – 3 ) ² + ( x – 3 ) 

So, if we have a point ( x , y ) on the function f ( x ), it will now be transformed to (x + 3, y ).

5. For transformation of f ( x ) to – f ( x ) , f ( x) is flipped upside down. This means that f ( x) is reflected about the x -axis. For example, if we have a function, f ( x ) = x² + x and we want reflect it over x-axis, the transformation of f ( x ) will be 

f ( x ) → – f ( x ) 

⇒ f ( x ) = –  ( x ) ² – x 

So, if we have a point ( x , y ) on the function f ( x ), it will now be transformed to (x , – y ).

6. For transformation of f ( x ) to  f (- x ) , f ( x) is the mirror of f ( – x ). This means that f ( x) is reflected about the y -axis. For example, if we have a function, f ( x ) = x² + x and we want reflect it over y-axis, the transformation of f ( x ) will be 

f ( x ) →  f ( – x ) 

⇒ f ( x ) =  ( – x ) ² + ( –  x ) 

So, if we have a point ( x , y ) on the function f ( x ), it will now be transformed to ( – x , y ).

Let us now learn about some basic parent functions

Absolute Value Parent Function

The absolute value function f ( x) is defined by

f ( x ) = | x | = {-x,  x<0   0,  x=0 x,  x>0

is called a absolute value function. It is also called a modulus function. We observe that the domain of the absolute function is the set R of all real numbers and the range is the set of all non-negative real numbers. This means that,

R⁺ = { x ∈ R : x ≥ 0 }

Graph of Absolute Value Function

The graph of the absolute value function is shown in the below figure.

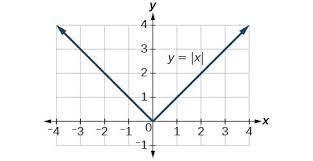
It is important to note here that for x > 0 the graph of the absolute value function coincides with the graph of the identity function, i.e. the line y =  x and for x < 0 it is coincident to the line y =  -x.

Linear Equation Parent Function

The parent function of a linear equation is f ( x ) = x. the graph of this function is given by  – 

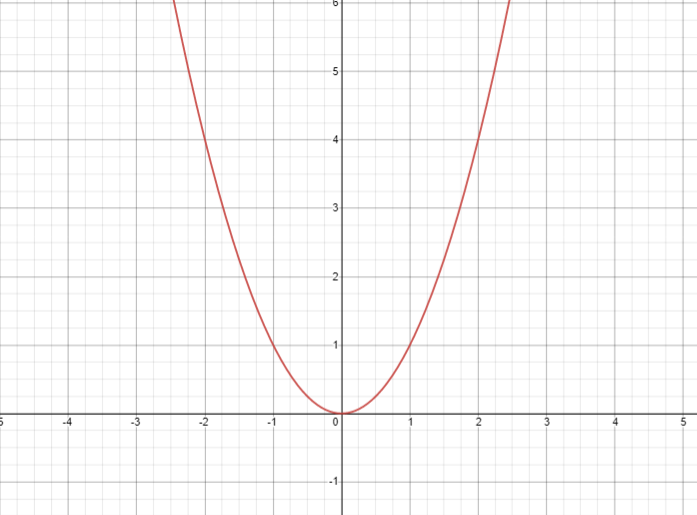
Quadratic Equation Parent Function

All quadratic functions have the highest exponent of 2, their graphs are all parabolas. The parent function of a quadratic equation is f ( x ) = x ². The graph of this function is given by  – 

Examples

Example 1 What Does the Transformation Given Below do to the Graph?

a) f ( x ) → f ( x ) – 2

b) f ( x ) → f ( x – 2 )

Solution a) f ( x ) → f ( x ) – 2

We can see that the y-coordinates of the function are being changed by 2 units. Let us recall that for transformation of f ( x ) to f ( x ) – a, f ( x) is shifted downwards by a units and if we have a point ( x , y ) on the function f ( x ), it will now be transformed to (x, y – a ). Therefore, we will have,

The transformation here is translation 2 units down.

b) f ( x ) → f ( x – 2 )

We can see that the x-coordinates of the function are being changed by 2 units. Let us recall that for transformation of f ( x ) to f ( x – a ) , f ( x) is shifted right by a units.

Hence, the transformation here is translation 2 units right.

Example 2 How is the Graph of y = ( x – 4 ) – 5 Related to the Graph of y =  f ( x ) ?

Solution When the graph of y =  f ( x ) is moved right by 4 units, we get y =  f ( x – 4 ). When the graph of y =  f ( x – 4 ) is moved down by 5 units, we get y= ( x – 4 )- 5 . Hence, the graph of y= ( x – 4 ) – 5 is located 4 units right, 5 units down of the graph of y = f ( x ) . Hence, the point ( x, y ) moves to ( x + 4, y – 5 ).

Key Facts and Summary

1. Transformations of functions mean transforming the function from one form to another.
2. There are four major types of transformations of functions – Translation, Rotation, Reflection and Dilation.
3. Translation transformation slides or moves the object in the space by keeping its size and orientation the same.
4. A rotation is a transformation that is performed by “spinning” the object around a fixed point known as the centre of rotation.
5. A reflection of a function causes the graph to appear as a mirror image of the original function.
6. Dilation or scaling is a transformation that changes the size and/or the shape of the graph of the function. It is the only manner in which we can change the size of the function.
7. For transformation of f ( x ) to f ( x ) + a, f ( x) is shifted upwards by a units.
8. For transformation of f ( x ) to f ( x ) – a, f ( x) is shifted downwards by a units.
9. For transformation of f ( x ) to f ( x + a ) , f ( x) is shifted left by a units.
10. For transformation of f ( x ) to f ( x – a ) , f ( x) is shifted right by a units.
11. For transformation of f ( x ) to – f ( x ) , f ( x) is flipped upside down.
12. For transformation of f ( x ) to  f (- x ) , f ( x) is the mirror of f ( – x ).