Union of Sets

Definition

Let A and B be two sets. The union of A and B is the set of all those elements which belong either to A or to b or to both A and B. The notation A U B, read as A union B, is used to denote the union of two sets A and B.

Thus A U B = { x : x ∈ A or x ∈ B }

Before we learn any further on this, let us recall what we mean by sets.

What is a set?

A set is a well-defined collection of objects. Here, by collection, we mean an aggregate of objects or things while aggregate itself means a class of things. Let a be an element of a set A. It is written as a belongs to A, which in symbolic form is written as a ∈ A. If a is any other element but does not belong to the set A, it is written as a does not belong to A, which in symbolical form is written as a ∉ A.

Let us understand it through an example.

Suppose wish to create a collection of the vowels of the English alphabet. We know that the vowels are a, e, i, o and u. Hence, the collection of vowels in the English alphabet will be a, e, i, o and u.

Some Standard Sets

In mathematics, we commonly refer to numbers as whole numbers, natural numbers etc. These numbers are standard sets of numbers based on their specific properties. Some of these standard sets are –

Natural Numbers – The set of natural numbers consists of numbers starting from 1, 2 , 3, ………. and so on. It is represented by N.

Whole Numbers – The set of whole numbers consists of numbers starting from 0, 1, 2 , 3, ……… and so on. It is represented by W.

Integers – The set of integers consists of numbers such as …….-3, -2, -1, 0, 1, 2 , 3……. and so on. It is represented by Z.

Rational Numbers – The set of rational numbers consists of numbers that can be represented in the form of $\frac{p}{q}$ where q ≠ 0. It is represented by Q.

Real Numbers – The set of integers consists of all real numbers such as …….-3, -2, -1, 0, 1, 2 , 3……. and so on. It is represented by R.

Types of sets

Let us now learn about different types of sets depending upon the elements they contain.

Empty set – A set is said to be an empty or null or void set if it has no element. Such a set is denoted by ∅. In roster form, ∅ is denoted as { }.

For example, if we wish to create a set consisting of all natural numbers less than 1. We know that there does not exist any such natural number which is less than 1. Hence, this set will be represented as A = { x : x ∈ N and x < 1 } = ∅ or { }

Finite Set – A set is called a finite set if it is either void or it has a fixed number of elements. For example, the set of the first five natural numbers which will be given by A = { 1, 2, 3, 4, 5 } is a finite set as it has 5 fixed elements.

Infinite Set – A set is called an infinite set if it does not have a fixed number of elements. For example, the set of natural numbers which will be given by A = { 1, 2, 3, ……….. } is infinite as it has an infinite number of elements.

Equal Sets – Two finite sets are said to be equal if they have the same elements. For example, the set A = { 1, 2 , 3, 4 } and the set B = { 1, 2 , 3, 4 } are equal.

Subsets – Let A and B be two sets. If every element of A is an element of B, then A is called the subset of B. If A is a subset of B, we write it as A ⊆ B. Thus, if A ⊆ B, iff

a ∈ A ⇒ a ∈ B

For example,

{ 1 } ⊂ { 1, 2, 3 } but { 1, 4 } ⊄ { 1 , 2, 3 }

Universal Set – In any discussion in set theory, there always happens to be a set that contains all sets under consideration, i.e. it is a superset of each of the given sets. Such a set is called the universal set and is denoted by U. thus a set that contains all sets in a given context is called the universal set.

Union of sets using Venn Diagram

Recall that Swiss mathematician, Euler, was the first to come up with a pictorial representation of sets. Later on British mathematician John Venn ( 1834 – 1883) brought this idea to practice. Named after these two mathematicians, we have Venn-Euler diagrams or simply Venn diagrams. Venn diagrams are the pictorial representation of the sets. In Venn diagrams, the universal set, U is represented by points within a rectangle. The subsets of the universal set are represented by points in circles within a rectangle.

Let us now learn how to represent the union of two sets through a Venn diagram. The shaded portion in yellow shown in the below Venn diagram represents the union of two sets A and B.

Let us understand it through an example.

Suppose we have two sets A = { 1, 2, 3, } and B = { 1, 3, 5, 7 }

What will be A U B ? Let us find out.

A U B will be given by the union of all elements belonging either to A or to B. hence,

A U B = { 1 , 2, 3, 5, 7 }

Another type of combination of sets that are important to learn along with the union of sets are the intersection of sets and complement of a set.

Intersection of Sets

Let A and B be two sets. The intersection of A and B is the set of all those elements which belong to both A and B. The notation A ∩ B, read as A intersection B, is used to denote the intersection of two sets A and B.

Thus A ∩ B = { x : x ∈ A and x ∈ B }

Let us now learn how to represent the intersection of two sets through a Venn diagram. The shaded portion in yellow shown in the below Venn diagram represents the intersection of two sets A and B.

Let us understand it through an example.

Suppose we have two sets A = { 1, 2, 3, } and B = { 1, 3, 5, 7 }

What will be A ∩ B ? Let us find out.

A ∩ B will be given by finding the common elements that belong both to A and B. Hence,

A ∩ B = { 3 }

Complement of a Set

Before we learn about the representation of complement of a set through the Venn diagram, let us learn what we mean by a complement of a set? Let U be the universal set and let A be a set such that A ⊂ U. then the complement of a with respect to U is denoted by A ‘ or A^c or U – A and is defined as the set of all those elements of U which are not in A.

Let us understand it through an example.

Suppose we have universal set U = { 1, 2, 3, 4, 5, 6, , 8, 9, 10 }

Let A be a subset of U such that A = { 1, 3, 5, 7, 9 }. Now the complement of A will be given by A ‘ = { 2, 4, 6, 8, 10 } which means all those elements that are present in the universals et but are not present in A.

Now, let us learn how to represent the complement of a set using a Venn diagram. The shaded portion in yellow shown in the below Venn diagram represents the complement of a set A.

Union of sets in intersecting circles

Let the universal set be the first 10 natural numbers.

Hence, let U = { 1, 2, 3, 4, 5, 6, , 8, 9, 10 }

Suppose we have two sets A and B where

A = { 1, 2, 3, 4, 5 } and B = { 1 , 3 , 5 , 7 , 9}

We can see that the two sets A and B have some elements in common. Therefore, they will be represented as intersecting circles. The common elements shall be placed in the common region of the two circles. Also, the elements that belong to the universal set but are not a part of any subset shall be listed separately.

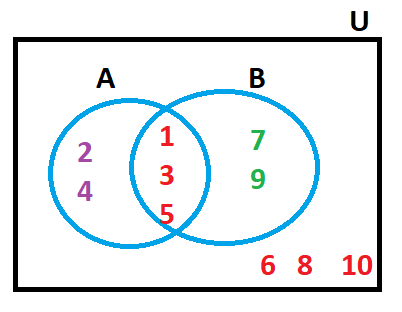
Now, what would be A U B?

We know that A U B will be given by the union of all elements belonging either to A or to B. hence,

A U B = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

Union of sets of disjoint circles

Again, let the universal set U = { 1, 2, 3, 4, 5, 6, , 8, 9, 10 }

Suppose we have two sets A and B where

A = { 1, 2, 3, 4, 5 } and B = { 6, 7, 8, 9, 10}

We can see that the two sets A and B have no element in common. Therefore, they will be represented as disjoint circles. The Venn diagram for this data will be represented as –

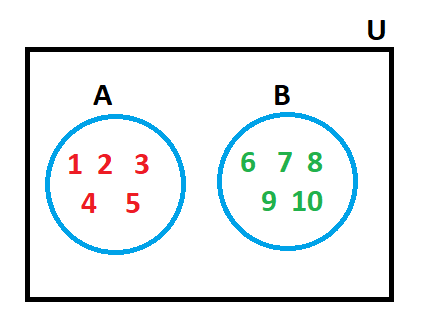
Now, what would be A U B?

We know that A B will be given by the union of all elements belonging either to A or to B. hence,

A U B = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

Therefore, we can see that it does not matter whether the two sets have any common elements or not. The union of two sets would always contain elements that belong either to A or to B or both A and B.

Solved Examples

Example 1 If A = { 1, 2, 3, 4, 5 }, B = { 4, 5, 6, 7, 8 }, C = { 7, 8, 9, 10, 11 }, find A U ( B ∩ C )

Solution We have been three sets where A = { 1, 2, 3, 4, 5 }, B = { 4, 5, 6, 7, 8 }, C = { 7, 8, 9, 10, 11 }. We have to find A U ( B ∩ C )

Let us first find the value of B ∩ C

Since, B = { 4, 5, 6, 7, 8 } and C = { 7, 8, 9, 10, 11 }

B ∩ C = { 7, 8 }

Since, A = { 1, 2, 3, 4, 5 } and from above, B ∩ C = { 7, 8 }, therefore,

A U ( B ∩ C ) = { 1, 2, 3, 4, 5, 7, 8 }

Example 2 Let A = { 3, 6, 12, 15, 18, 21 }, B = { 4, 8, 12, 16, 20 ], C = { 2, 4, 6, 8, 10, 12, 14, 16 }, find the value of A U ( B U C )

Solution We have been given that A = { 3, 6, 12, 15, 18, 21 }, B = { 4, 8, 12, 16, 20 ], C = { 2, 4, 6, 8, 10, 12, 14, 16 }. We need to find the value of A U ( B U C )

Let us first find the value of B U C

Since, B = { 4, 8, 12, 16, 20 ] and C = { 2, 4, 6, 8, 10, 12, 14, 16 }, therefore,

B U C = { 2, 4, 6, 8, 10, 12, 14, 16, 20 }

Since A = { 3, 6, 12, 15, 18, 21 } and from above, B U C = { 2, 4, 6, 8, 10, 12, 14, 16, 20 }, therefore,

A U ( B U C ) = { 2, 3, 4, 6, 8, 10, 12, 14, 15, 16, 18, 20, 21 }

Laws of Algebra of sets involving union of sets

Below we have some laws of algebra of sets that involve the union of sets –

For any set A, the intersection of a set A with itself results in the same set, i.e. A U A = A
For any set A, the union of a set A with empty set results in the same set, i.e. A U ∅ = A
For any two sets A and B, the union of two sets A and B satisfies the commutative property, i.e. A U B = B U A
For any three sets A, B and C, the union of three sets A, B and C satisfies the associative property, i.e. ( A U B ) U C = ( A U ( B U C )
For any three sets A, B and C, the intersection of three sets A, B and C satisfies the associative property, i.e. ( A ∩ B ) ∩ C = ( A ∩ ( B ∩ C )
For any three sets A, B and C, the union and intersection of three sets A, B and C satisfies the distributive property, i.e. ( A U ( B ∩ C ) = ( A U B ) ∩ ( A ∪ C )

Key Facts and Summary

Let A and B be two sets. The union of A and B is the set of all those elements which belong either to A or to b or to both A and B.
A set is a well-defined collection of objects.
The union of A and B is the set of all those elements which belong either to A or to b or to both A and B. The notation A U B, read as A union B, is used to denote the union of two sets A and B.
The intersection of A and B is the set of all those elements which belong to both A and B. The notation A ∩ B, read as A intersection B, is used to denote the intersection of two sets A and B.
Let U be the universal set and let A be a set such that A ⊂ U. then the complement of a with respect to U is denoted by A ‘ or A ^c or U – A and is defined as the set of all those elements of U which are not in A.
For any set A, the intersection of a set A with itself results in the same set, i.e. A U A = A
For any set A, the union of a set A with empty set results in the same set, i.e. A U ∅ = A
For any two sets A and B, the union of two sets A and B satisfies the commutative property, i.e. A U B = B U A
For any three sets A, B and C, the union of three sets A, B and C satisfies the associative property, i.e. ( A U B ) U C = ( A U ( B U C )
For any three sets A, B and C, the intersection of three sets A, B and C satisfies the associative property, i.e. ( A ∩ B ) ∩ C = ( A ∩ ( B ∩ C )
For any three sets A, B and C, the union and intersection of three sets A, B and C satisfies the distributive property, i.e. ( A U ( B ∩ C ) = ( A U B ) ∩ ( A ∪ C )

Recommended Worksheets

Whole Numbers (Rio Carnival Themed) Math Worksheets
Set and Set Notation (Supermarket Themed) Worksheets
Spatial Skill: Circles (New Year’s Eve Themed) Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!