Distance Between Two Points on a Number Line
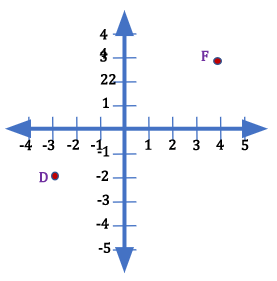
Getting the distance between two points is finding out how far apart these points are. Let us look at the illustration below and find out how the points D and F are far apart from each other.

The number line at the left shows that the points are 5 units apart. The number line on the right tells us that the points are 7 units apart. The difference in the numbers based on their locations gave us an idea of how far apart these points are. Such that,
3-(-2)=3+2=5 units and
4-(-3)=4+3=7 units
So, if we have points D and F on the number line with coordinates p and q respectively, then the distance between these points is given by,
d (DF) = | p-q | or d (DF) = | q-p |
Notice that p and q can be placed in the formula in any order. The use of absolute value and the computed distance is always positive. Remember that when we think absolute value, we are looking at the distance between a number and zero (0) on the number line.
Let us try these examples:
- Find the distance between 8 and -5.
d= | 8- (- 5) |d= 8| + 5 |d= |13 |d= 13
Thus, 8 and-5 are 13 units apart.
- Find the distance between these integers: -4 and -12.
d= |-12 – (-4) |d= -12| +4 |d= |-8 |d= 8
Hence, the distance between -4 and -12 is 8 units.
- What is the distance between points -8 and 8?
d= | 8 – (-8 ) | d= | 8 +8|d= |16| d= 16
Therefore, -8 and 8 are 16 units apart.
- What is the distance between points 10 and -18?
d= | 10- (-18 ) |d= | 10 +18|d= |28|d= 28
Thus, the distance between10 and -18 is 28 units.
What if these points are located like the illustration below? How do we then solve for the distance between these points?
Distance Formula
The distance formula is the formula we use to calculate the distance between points in terms of their coordinates.
d= $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
where;
( x1, y1 ) and ( x2, y2 ) are the coordinates of the two given points
Derivation of the Distance Formula
Let us say that the coordinates of points D and F are ( x1, y1 ) and ( x2, y2 ), respectively.
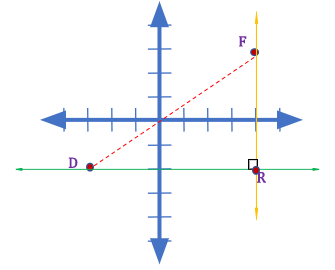
Now draw a line horizontal line that passes through point D. Draw also a vertical line that passes through point F. Let R be the intersection of these lines. As shown in the illustration, these lines form a right triangle with the hypotenuse line segment DF.
Hence, DR=( x2-x1 ) , FR=( y2-y1 ) and DF is the hypotenuse.
Thus, by Pythagorean Theorem, c2= a2 + b2, we
( DF )2= ( DR )2 + ( FR )2
( DF )2= ( x2-x1 )2+ ( y2-y1 )2
DF= $\sqrt{(x_2 – x_1)^2 + (y_2-y_1)^2}$
To denote the distance solved using the distance formula, we usually use the letter d.
The Distance Formula
d= $\sqrt{(x_2 – x_1)^2 + (y_2-y_1)^2}$
Steps in Getting the Distance Between Two Points
These are the steps in getting the distance between two points in a coordinate system if d is the distance between two points ( x1, y1 ) and ( x2, y2 ).
Steps in Getting the Distance Between two Points
Step 1: Label the given coordinates as ( x1, y1 ) and ( x2, y2 ).
Step 2: Solve the horizontal distance by getting the difference between x1 and x2.
Step 3: Solve the vertical distance by getting the difference between y1 and y2.
Step 4: Square the horizontal distance and the vertical distance separately.
Step 5: Get the sum of the squared values.
Step 6: Take the square root of the answer in Step 5 and simplify.
Applying the Distance Formula, we have:
Step 1: Label: ( x1, y1 ) and ( x2, y2 )
Step 2: Horizontal distance: ( x2-x1 )
Step 3: Vertical Distance: (y2-y1)
Step 4 : Square of the horizontal distance: (x2-x1)2
Square of the vertical distance: ( y2-y1 )2
Step 5: Sum of the squared values: ( x2-x1 )2+ ( y2-y1 )2
Step 6: Square root of the answer in Step 5: $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
Examples
Example 1: What is the distance between the points ( 1, 3 ) and 4, 7 ?
Solution: Let us follow the steps in getting the distance between two points.
Step 1: Label the given coordinates as ( x1, y1 ) and ( x2, y2 ).
x1=1 y1=3 x2=4 y2=7
Step 2: Solve the horizontal distance by getting the difference of x1 and x2.
Horizontal distance: 4-1=3
Step 3: Solve the vertical distance by getting the difference of y1 and y2.
Vertical distance: 7-3=4
Step 4: Square the horizontal distance and the vertical distance separately.
Square of the horizontal distance: 32= 9
Square of the vertical distance: 42= 16
Step 5: Get the sum of the squared values.
9 + 16=25
Step 6: Take the square root of the answer in Step 5.
√25= 5
Therefore, the distance between the points 1, 3 and ( 4, 7 ) is 5 units.
If we answer the problem straight to the distance formula, this is how it look like:
d= $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
d= $\sqrt{(4-1)^2 + (7-3)^2}$
d= $\sqrt{(3)^2 + (4)^2}$
d= $\sqrt{9 + 16}$
d= $\sqrt{25}$
d= 5
Is it correct to use the point 4, 7 as ( x1, y1 ) and the ( 1, 3 ) as ( x2, y2 ) instead?
Alternative solution: x1=4, y1=7, x2=1, y2=3
d= $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
d= $\sqrt{(1-4)^2 + (3-7)^2}$
d= $\sqrt{(-3)^2 + (-4)^2}$
d= $\sqrt{9 + 16}$
d= $\sqrt{25}$
d= 5
For as long as you properly label your coordinates and follow their correct placement in the distance formula, you will still get the correct answer.
Example 2: Find the distance between the points -2, -5 and ( 3, -4 ).
Solution:
Let us label the given coordinates. x1=-2, y1=-5 , x2=3, and y2=-4
Using distance formula, we have:
d= $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
d= $\sqrt{[3- (-2 )]^2 + [-4- (-5)]^2}$
d= $\sqrt{(3 + 2)^ 2+ (-4 + 5)^2}$
d= $\sqrt{5^2 +(1)^2}$
d= $\sqrt{25 + 1}$
d= $\sqrt{26}$
d≈ 5.10
Thus, the distance between the points -2, -5 and ( 3, -4 ) is 26 units.
Example 3: Find the distance between the points -8, -3 and ( -1, -9 ).
Solution:
Let us label the given coordinates. x1=-8, y1=-3 , x2=-1, and y2=-9.
Let us now get the distance between these points using the distance formula. The given coordinates are all negative integers so be careful when substituting these values in the formula.
d= $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
d= $\sqrt{[-1- (-8 )]^2 + [-9- (-3)]^2}$
d= $\sqrt{(-1+8)^2 + (-9+3)^2}$
d= $\sqrt{(7)^2+ (-6)^2}$
d= $\sqrt{49 + 36}$
d= $\sqrt{85}$
d≈ 9.22
Hence, the distance between the points -8, -3 and ( -1, -9 ) is 85 units.
Example 4: What is the distance between the points ( 4, 8 ) and ( -3, 8 )?
Solution: Using the distance formula,
d= $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
d= $\sqrt{(-3-4)^2+ (8-8)^2}$
d= $\sqrt{(-7)^2 + (0)^2}$
d= $\sqrt{49+0}$
d= $\sqrt{49}$
d= 7
If we plot these points, we can see that they are horizontally aligned as shown in the figure below.
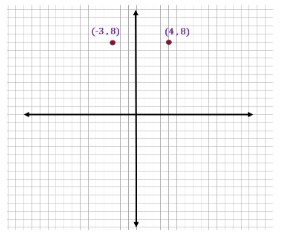
Thus, if the given points have the same y-coordinates, then these points are horizontally aligned. To get the distance between these points, we may simply get the absolute value of the horizontal distance.
Formula in getting the distance between two points horizontally aligned:
d = | x2-x1 | or d = | x1-x2 |
Using this formula instead we may have,
d = | -3-4 |
d = | 4- (-3) |
d = | -7 |
d = | 4+3 |
d= 7
Example 5: Determine the distance between the points ( 2, 7 ) and 2, -1 .
Solution: If we let x1=2, y1=7, x2=2 and y2=-1, we will have this solution:
d= $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
d= $\sqrt{(2-2)^2+ (-1-7)^2}$
d= $\sqrt{(0)^2 + (-8)^2}$
d= $\sqrt{0+64}$
d= $\sqrt{64}$
d = |8|
d= 8
The figure below shows the location of these points on the coordinate system.

Thus, if the given points have the same x-coordinates, then these points are vertically aligned. To get the distance between these points, we may simply get the absolute value of the vertical distance.
The formula in getting the distance between two points vertically aligned:
d=| y2-y1 | or d=| y1-y2 |
Using this formula instead we may have,
d = | -1-7 |
d = | 7- (-1) |
d = | -8 |
d = | 7+1 |
d = |8|
d =8
Therefore, the distance between the points ( 2, 7 ) and ( 2, -1 ) is 8 units.
Example 6: A subdivision, where Marivic and Erica live, uses a coordinate system mapping with the Club House at the origin. Marivic’s house is located at ( 5, -4 ) and Erica’s house is located at -7, 3 . How far is it from Marivic’s house to Erica’s house?
Solution: The figure below shows the location of the houses of Marivic and Erics on a coordinate system.
Let us say that (x1,y1) is the location of Marivic’s house and ( x2,y2 ) is the location of Erica’s house, using distance formula we have,
d= $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
d= $\sqrt{( -7-5 )^2+ [3- (-4 )]^2}$
d= $\sqrt{(-12)^2+ (7)^2}$
d= $\sqrt{144+49}$
d= $\sqrt{193}$
d≈13.89
Therefore, the distance between their houses is 13.89 units.
Example 7: The coordinates of two points are ( 1, y ) and ( 7, -2 ). Find the value of y such that the distance between two points is 10 units.
Solution: Let us use the distance formula to find the value of y.
x1=1 y1=y x2=7 y2=-2 d=10 units
$\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
=d $\sqrt{(7-1)^2 +(-2-y)^2}$
=10$\sqrt{(6)^2+( 4+4y+y^2 )}$
=10$\sqrt{36+4+4y+y^2}$
=10$(\sqrt{(40+4y+y^2)})^2$
=102(40+4y+y2)
=100-100+40+4y+y2
=0y2+4y-60
=0(y -6) (y+10)
=0
y-6= 0 y+10= 0 y= 6 y= -10
The y-values are 6 and -10. Hence, the point ( 7, -2 ) is 10 units away from the points ( 1 , 6 ) and ( 1, -10 ).
Example 8: The locations of four computers in a room are represented by lettered points in the coordinate system. These points are A( 0, 14 ), B( 4 ,2 ), C( 6, 16 ) and D( 10, 4 ). Show that the positions of these points form a rectangle.
Solution. The graph below shows the positions of computers A, B, C, and D on the coordinate system.

The two pairs of opposite sides are sides AB and CD , and sides AC and BD. We must get the distance of the sides AB, AC, BD, and CD using distance formula.
d (AB) = $\sqrt{( 4-0 )^2+ (2-14)^2}= \sqrt{4^2+ (-12)^2}= \sqrt{16+144}= \sqrt{160}= \sqrt{16⋅10}
d (AB) = 4\sqrt{10}$
d (AC) = $\sqrt{( 6-0 )^2+ (16-14)^2}= \sqrt{6^2+(2)^2}= \sqrt{36+4}= \sqrt{40}= \sqrt{4⋅10}
d (AC) = 2\sqrt{10}$
d (BD) = $\sqrt{( 10-4 )^2+ (4-2)^2}= \sqrt{6^2+ (2)^2}= \sqrt{36+4}= \sqrt{40}= \sqrt{4⋅10}
d (BD)=2\sqrt{10}$
d (CD) = $\sqrt{( 10-6 )^2+ (4-16)^2}= \sqrt{4^2+ (-12)^2}= \sqrt{16+144}= \sqrt{160}= \sqrt{16⋅10}$
d (CD) = $4\sqrt{10}$
Since d AC =d( BD ) and d AB =d( CD ), this confirms that the locations of the computers form a rectangle.
Example 9: If the endpoints of a line segment are ( x, y) and the origin, find a formula to get the distance between them.
Solution: Use the coordinates of the endpoints of the line segment as ( x,y ) and ( 0, 0 )
Using distance formula we have,
d= $\sqrt{(x -0)^2+ (y-0)^2}$
d= $\sqrt{x^2+y^2}$
Therefore, d=$\sqrt{x^2+y^2}$ is the formula for the distance between the origin and a point on a rectangular coordinate system.
Example 10: Find the perimeter of ∆YNA. The coordinates of the vertices are Y (-6, -2) , N( 0, 8 ) and A( 5 , -4 ).
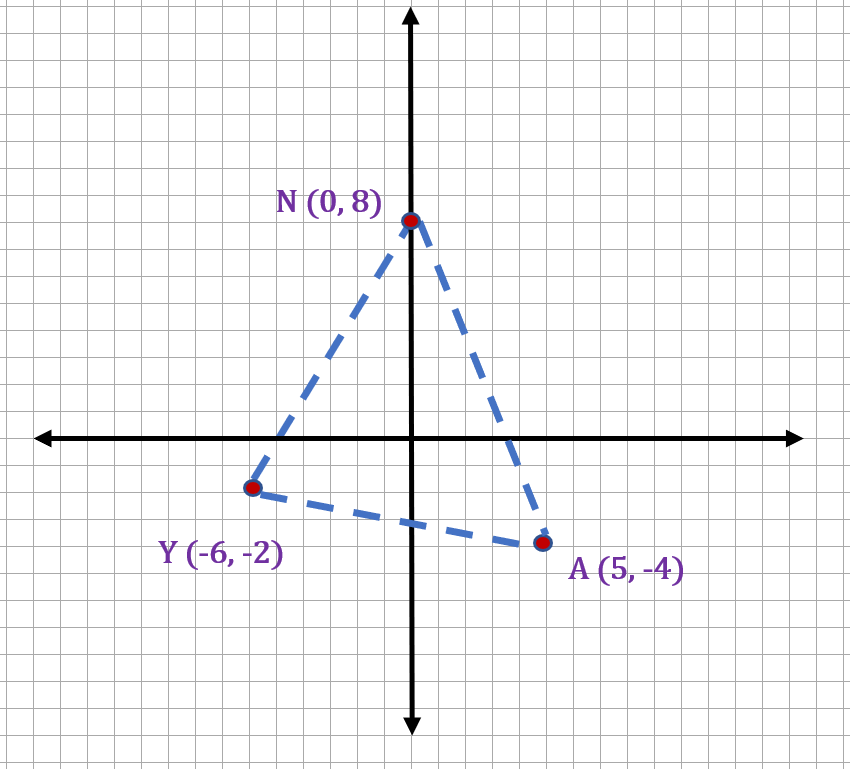
Solution: To get the perimeter of ∆YNA, we need to get the total of all the lengths of its sides. As such, let us use the distance formula to get the length of each side of the given triangle. We must compute the following distances: YN, AN, and AY.
d (YN) = $\sqrt{( -6-0 )^2+ (-2-8)^2}= \sqrt{( -6 )^2+ (-10)^2}= \sqrt{36+100}= \sqrt{136}= \sqrt{4⋅34} d (YN) =2\sqrt{34}$
d (AN) = $\sqrt{( 0-5 )^2+8-( -4 )^2}= \sqrt{25+144}= \sqrt{169}$ d (AN) =13
d (AY) = $\sqrt{( -6-5 )^2+ (-2-(-4) )^2}= \sqrt{(-11)^2+ (-2+4)^2}= \sqrt{(-11)^2+ (2)^2}= \sqrt{121+4}= \sqrt{125}= \sqrt{25⋅5} d (AY) = 5\sqrt{5}$
Therefore, the perimeter of ∆YNA is $13+2\sqrt{34}+5\sqrt{5}$ units or approximately 35.84 units.
Midpoint
Suppose we have drawn a line segment joining the points D and F.
To find the midpoint, we may get the distance between the points D and F and divide it by two ( 2 ). For example,
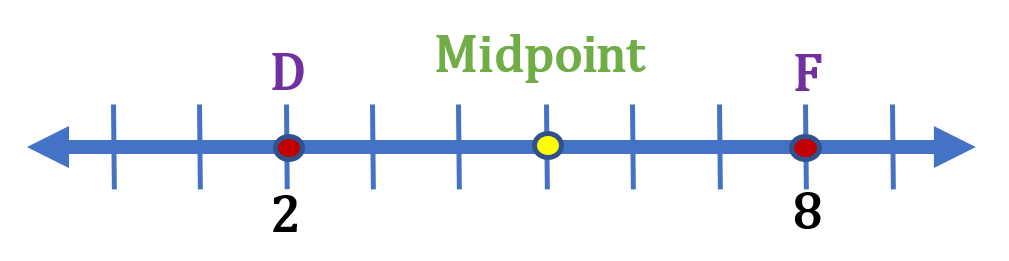
So, to get the midpoint of 2 and 8 we have, $\frac{2+8}{2}=\frac{10}{2}=5$. This is the same as getting the average of 2 and 8.
Midpoint Formula
Let us say that we have points D (x1, y1) and F(x2,y2), then we can calculate its midpoint by using this formula:
$\frac{x_1 + x_2 }{2}, \frac{y_1 + y_2}{2}$
Examples
Example 1: Using the midpoint formula, calculate the midpoint between the points A 2, 7 and B ( 4, 5 ).
Solution: Let x1=2 y1=7 x2=4 y2=5
Using the midpoint formula we have,
= $(\frac{2+4}{2}, \frac{5+7}{2}) = (\frac{6}{2} , \frac{12}{2}) = (3, 6)$
Therefore, the coordinates of the midpoint between the points A 2, 7 and B ( 4, 5 ) is 3, 6 .
Example 2: Find the midpoint between the points P (-1,-8) and Q ( -3, -5 ).
Solution: Let x1=-1 y1=-8 x2=-3 y2=-5
Using the midpoint formula we have,
= $(\frac{-1+( -3 )}{2} ,\frac{-8+ (-5)}{2}) = (\frac{-4}{2} ,\frac{-13}{2}) = (-2, -\frac{13}{2})$
Hence, the coordinates of the midpoint between the points P (-1,-8) and Q ( -3, -5 ).
is $(-2,-\frac{13}{2})$ .
Example 3: What is the midpoint of the line segment that connects S 10,-5 and T ( 6, 1 ).
Solution: Let x1=10 y1=-5 x2=6 y2=1
Using the midpoint formula we have,
= $(\frac{10 +6}{2} , \frac{-5 +1}{2}) = (\frac{16}{2} ,\frac{-4}{2})= (8, -2)$
Thus, the coordinates of the midpoint that connects the line segment S (10, -5) and T ( 6, 1 ).
is 8,-2 .
Example 4: The midpoint of DF is point M( 6, 2 ). Find the coordinates of point D if the coordinates of point F are 8, 6 .
Solution: Since we already know the midpoint and an endpoint of the segment, let us use the midpoint formula to find the other endpoint.
Let D (x1, y1 ) be the missing endpoint and F 8, 6 be x2, y2 .
Midpoint of DF= $\frac{x_1+x_2}{2} ,\frac{y_1+y_2}{2}$
To find the x-coordinate of point D:
6=$\frac{x_1+8}{2}$12=x1+812-8=x14=x1
To find the y-coordinate of point D:
2=$\frac{y_1+6}{2}$4=y1+64-6=y1-2=y1
Thus, the coordinates of D are (4, -2) .
Example 5: Find the radius of a circle with a diameter whose endpoints of a diameter are at ( 5, -5 ) and -7 , 4 .
Solution: Let us use the midpoint formula to find the center of the circle using the endpoint of the given diameter.
Center= $(\frac{5+(-7)}{2} , \frac{-5+4}{2}) = (\frac{-2}{2} , \frac{-1}{2})=(-1, -\frac{1}{2})$
Since the center of the circle is at (-1, -1/2) , we will solve for the radius by getting the distance of the center to either of the given endpoints of the diameter.
Thus,
radius= $\sqrt{(5- (-1))^2+(-5-(-\frac{1}{2}))^2}= \sqrt{(5+1)^2+ (-5 + \frac{1}{2})^2}= \sqrt{( 6 )^2+ (- \frac{9}{2})^2}= \sqrt{36 + \frac{81}{4}}= \sqrt{\frac{144+81}{4}}= \sqrt{\frac{225}{4}} =\frac{15}{2}$
Therefore, the radius of the given circle is $\frac{15}{2}$ units.
Let us try to solve this by getting the distance of the diameter of the circle. Since the endpoints are ( 5, -5 ) and -7 , 4 , we have,
d= $\sqrt{(5- (- 7))^2+ (- 5-4)^2} d= \sqrt{(5+7)^2+ (- 9 )^2} d= \sqrt{(12)^2+81} d= \sqrt{144 + 81} d= \sqrt{225} d= 15$
Thus, the radius of the given circle is $\frac{diameter}{2}=\frac{15}{2}$ units.
Summary
Distance Between Two Points on a Number Line
If we have points D and F on the number line with coordinates p and q respectively, then the distance between these points is given by
d (DF) = | p-q | or d(DF)= | q-p |
If when we think about absolute value, we are looking at the distance between a number and zero (0) on the number line. Therefore, we get the distance between two points, we do not get a negative answer, or the answer is always positive.
Steps in Getting the Distance Between two Points
Step 1: Label the given coordinates as ( x1 , y1 ) and ( x2 , y2 ).
Step 2: Solve the horizontal distance by getting the difference between x1 and x2.
Step 3: Solve the vertical distance by getting the difference between y1 and y2.
Step 4: Square the horizontal distance and the vertical distance separately.
Step 5: Get the sum of the squared values.
Step 6: Take the square root of the answer in Step 5.
Applying the Distance Formula, we have:
Step 1: Label: ( x1 , y1 ) and ( x2 , y2 ).
Step 2: Horizontal distance: (x2-x1)
Step 3: Vertical Distance: (y2-y1)
Step4 : Square of the horizontal distance: (x2-x1)2
Square of the vertical distance: (y2-y1)2
Step 5: Sum of the squared values: ( x2-x1)2+(y2-y1)2
Step 6: Square root of the answer in Step 5: $\sqrt{( x_2-x_1)^2+(y_2-y_1)^2}$
The Distance Formula
d = $\sqrt{( x_2-x_1)^2+(y_2-y_1)^2}$
The formula in getting the distance between two points vertically aligned:
d =| y2-y1 | or d=| y1-y2 |
The formula in getting the distance between two points horizontally aligned:
d =| x2-x1 | or d=| x1-x2 |
The formula in getting the distance between the origin ( 0, 0) and a point
d= $\sqrt{x^2+y^2}$
The Midpoint Formula
$\frac{x_1+x_2}{2} ,\frac{y_1+y_2}{2}$
Recommended Worksheets
Distance Formula of Two Points 6th Grade Math Worksheets
Number Line Estimation (Wimbledon Themed) Math Worksheets
Measure of Distance using Standard Units (Veterans Day Themed) Worksheets









