Geometry Formulas Triangles

Introduction

We frequently encounter triangles in the real world, which are two-dimensional (2D) shapes with three sides and three angles.

A triangle is a three-sided polygon in geometry that has three edges and three vertices. One of the most significant characteristics of triangles is the sum of their internal angles is equal to 180 degrees.

In this article, you will find more about triangles, their properties and different formulas for finding specific measurements.

What are triangles?

Definition

Triangles are polygons with three (3) sides and (3) interior angles. It is denoted by the symbol △. 

Parts of a Triangle

A triangle has three (3) vertices, three (3) sides, and three (3) angles. In the triangle below, we have the following:

The three vertices are L, M, and N.

The three sides are side LM, side MN, and side NL.

The three angles are ∠LMN, ∠MLN, and ∠NLM. 

Classification of Triangles

Triangles are classified by their sides and angles. Triangles can be categorized as scalene, isosceles, or equilateral based on the lengths of their sides. Triangles can be acute, obtuse, or right, depending on their angles. 

The table below illustrates how triangles are categorized based on their sides and angles.

Classification of Triangles by their Sides	Classification of Triangles by their Angles
Equilateral Triangle 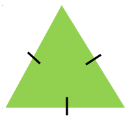An equilateral triangle has three equal-length sides.	Acute Triangle 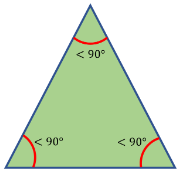Angles in an acute triangle are all less than 90 degrees.
Isosceles Triangle 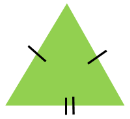Two of the sides of an isosceles triangle are of identical length.	Right Triangle 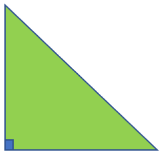One side of a right triangle is 90 degrees in angle.
Scalene Triangle 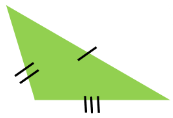A scalene triangle has no equal sides.	Obtuse Triangle An obtuse triangle has an angle that is higher than 90 degrees.

Sum of the Angles of a Triangle

A triangle’s internal angles are always added up to 180 degrees. 

Sum of the ∠s of a Triangle = ∠1 + ∠2 + ∠3 = 180°

Example

Find the measure of the missing angle x below.

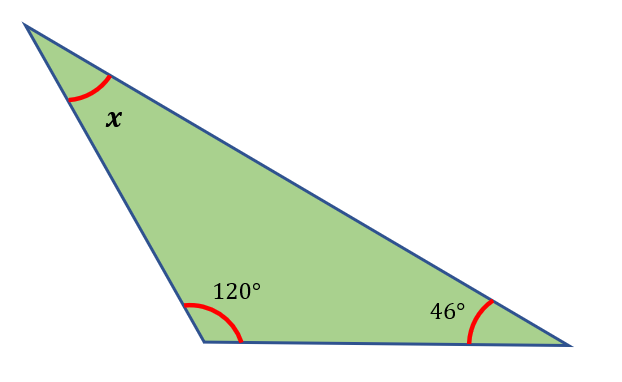
Solution

Since a triangle’s total angles equal 180 degrees, we obtain,

x + 120° + 46° = 180°
x + 166° = 180°
x = 180° – 166° 
x = 14°

Therefore, the missing angle x measures 14°.

The Perimeter of a Triangle

A triangle’s perimeter is equal to the sum of its sides. Let us say, for example, in the illustration below; the perimeter can be calculated using the formula,

Perimeter = x + y + z

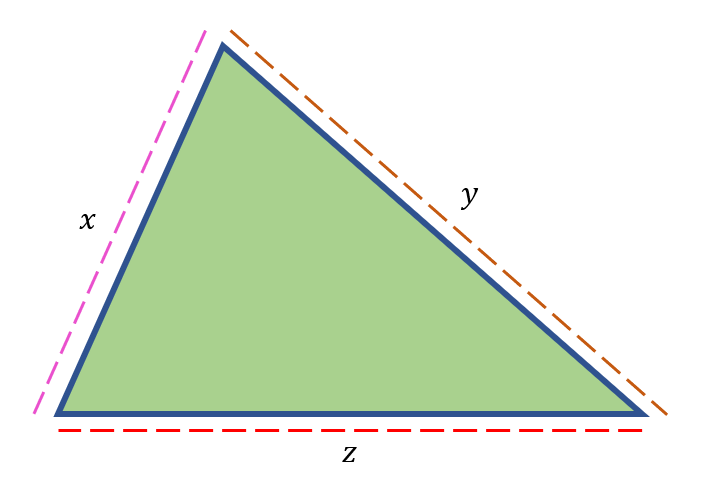
Example

Find the perimeter of the triangle shown below.

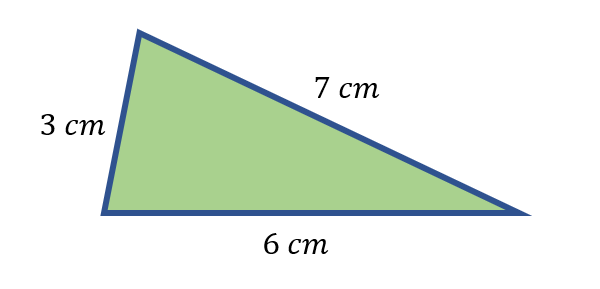
Solution

Since the perimeter of a △ is the sum of all three sides, we have,

Perimeter = 3 cm + 6 cm + 7 cm
Perimeter = 16 cm

Therefore, the perimeter of the triangle is 16 cm.

Area of a Triangle

The region bounded by a triangle’s perimeter, or its three sides, is known as the triangle’s area.

Base and height are known

It is determined by taking the product of the triangle’s base and height and dividing it by two. It is always measured in square units. 

Area of a Triangle = ½ × base × height

Let us say in the illustration below the base if NM while the height is LO. Thus, the area is the triangle is given by,

Area of ∆LMN = ½ × NM × LO

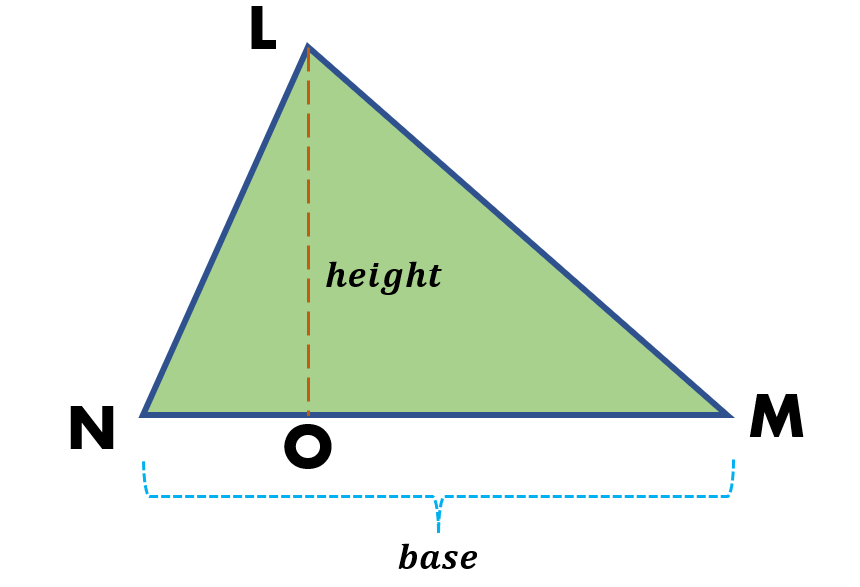
For example, we want to find the area of the triangle below,

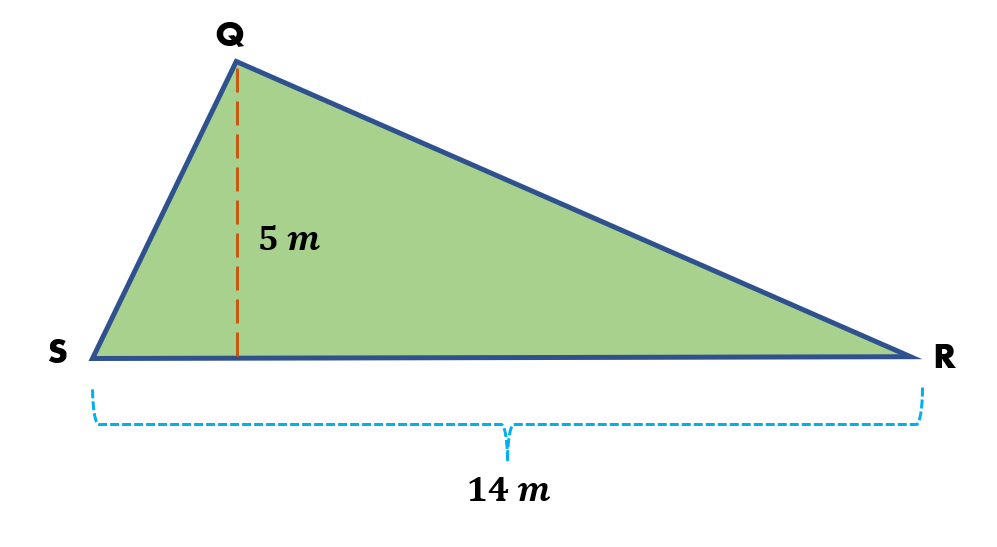
To calculate the area of ∆QRS, we have,

Area of ∆QRS = ½ × 14 m × 5 m 
Area of ∆QRS = ½ × 70 m²
Area of ∆QRS = 35 m²
Hence, the area of ∆QRS is 35 m².

Heron’s Formula

Given is Heron’s formula for calculating the area of a scalene triangle.

Area=$\sqrt{S (S – a)(S – b)(S – c)}$

where the variable S is the semi-perimeter, and the sides are a, b, and c.

The formula S=$\frac{a+b+c}{2}$ gives the semi-perimeter S.

For example, we want to solve the area of a scalene triangle with sides that are 81, 93, and 121 cm long.

Solution:

Let us find the semi-perimeter of the scalene triangle by using the formula S=$\frac{a+b+c}{2}$. Hence, we have,

S=$\frac{81+93+121}{2}$

S=$\frac{295}{2}$

S=147.50 cm.

Since we already know that the semi-perimeter of the given scalene triangle is 147.50 cm., let us now use Heron’s formula to find its area.

Area=$\sqrt{S (S-a)(S-b)(S-c)}$

Area=$\sqrt{147.50 (147.50-81)(147.50-93)(147.50-121)}$

Area=$\sqrt{147.50 ( 66.50)(54.50)(26.50)}$

Area=$\sqrt{14166287.19}$

Area≈3763.81 cm2

Therefore, the area of the given scalene triangle is 3763.81 square centimetres.

Pythagorean Theorem

The Pythagorean theorem, also known as Pythagoras’ theorem, states that at a right angle, the square on the hypotenuse (the side across from the right angle) equals the total of the squares on the two smaller sides. Hence, we use the formula,

a² + b² = c²

where side c is the length of the hypotenuse while a and b are the other two sides.

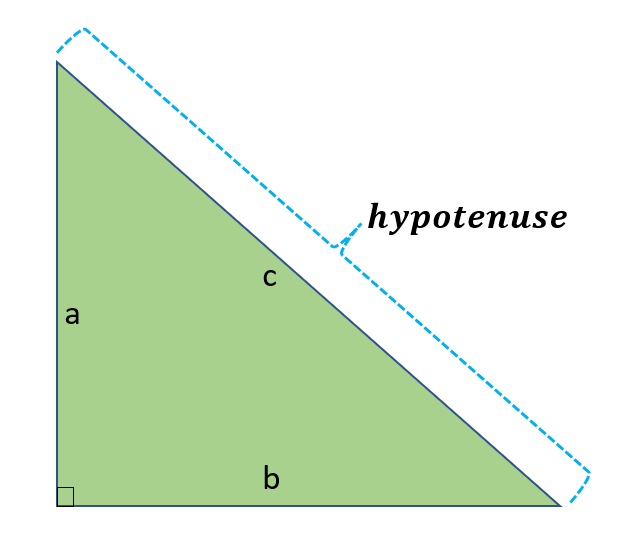
To further explain this, let us look at the image below,

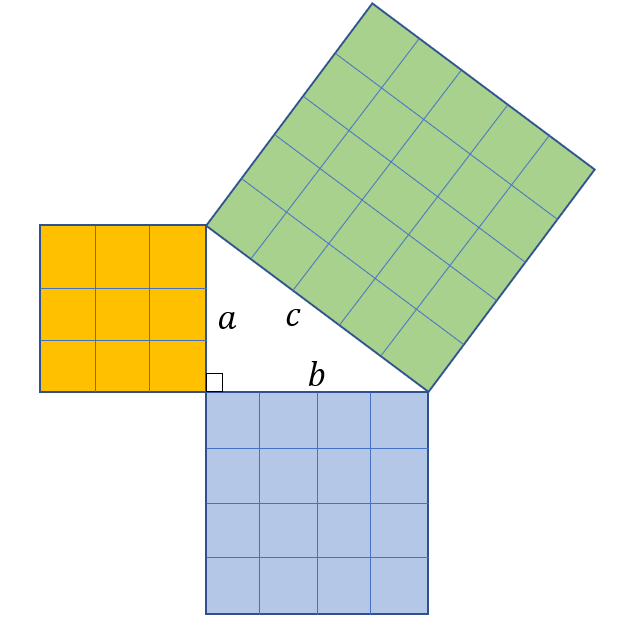
We can see that we have three squares with side lengths a, b, and c. Notice that we have a right triangle formed using these lengths. Let us say that side a has 3 units, and side b has 4 units. By Pythagorean Theorem, we can calculate side c.

c² = a² + b² 
c² = 3² + 4²
c² = 9 + 16
c² = 25
c = $\sqrt{25}$
c = 5

Consequently, the hypotenuse, or the longest side of the right triangle, is 5 units long. 

From the square tiles, it can be seen that the area of the yellow square ( 9 square units ) and the area of the blue square (16 square units ) is equal to the area of the green square ( 25 square units).

Here are the formulas when getting the lengths of the sides of a right triangle using the Pythagorean Theorem.

c=$\sqrt{a^2+b^2}$

a=$\sqrt{c^2-b^2}$

b=$\sqrt{c^2-a^2}$

Examples

Example 1

If the other two sides of a right triangle are 8 cm and 15 cm long, determine the hypotenuse length.

Solution

Let us say that side a = 8 am and side b = 15. Hence, to calculate the hypotenuse length, let us use the Pythagorean formula, c² = a² + b².

c² = a² + b² 
c² = 8² + 15²
c² = 64 + 225
c² = 289
c = 289
c = 17

Thus, the length of the hypotenuse is 17 cm.

Example 2

Find the length of the base of the right triangle below.

Solution

In the right triangle, we know that the hypotenuse length (the side opposite the right angle) is 10 cm, and the height is 8 cm. Let us say that a = 8 cm and c = 10 cm.

Therefore, by Pythagorean Theorem, to calculate the base of the right triangle, we have,

b² = c² – a²
b² = 10² – 8²
b² = 100 – 64 
b² = 36
b = 36
b = 6

As a result, the right triangle’s base measures 6 cm in length.

Basic Trigonometric Functions

The three basic trigonometric functions with right triangles are sine, cosine, and tangent.

Let us use the illustration below to become familiar with the parts and the basic trigonometric functions sine, cosine, and tangent.

∟ used to represent the right angle of the triangle

θ (theta) is used to represent one of the angles in the right triangle but not the right angle

o is used to represent the opposite side  of the angle θ

a is used to represent the adjacent side of the angle θ

h is used to represent the hypotenuse of the right triangle

For the three basic trigonometric functions, we use the mnemonic device: SOH CAH TOA, where S is for sine, C is for cosine, and T is for tangent. 

The formulas for the three basic trigonometric functions are given:

θ=$\frac{opposite}{hypotenuse}$	sin =$\frac{o}{h}$
cosine θ=$\frac{adjacent}{hypotenuse}$	cos θ=$\frac{a}{h}$
tangent θ=$\frac{opposite}{adjacent}$	tan θ=$\frac{o}{a}$

Examples

Example 1

Find the length of the opposite side of angle θ.

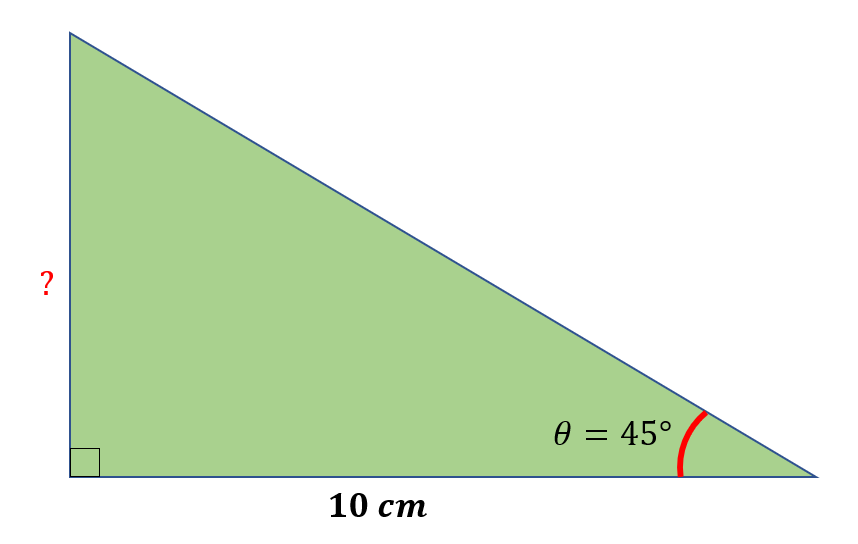
Solution

We know from the given data that θ=45° and the length of the adjacent side is 10 cm. Since the parts involved are the angle , the opposite side and the adjacent side, we will use the formula tan θ=$\frac{o}{a}$. Hence, we have,

tan θ=$\frac{opposite}{adjacent}$

tan 45°=$\frac{opposite}{10 cm}$

( 45° ) 10 cm =opposite

( 1 )( 10 cm )=opposite

10 cm=opposite

Example 2

Find the length of the hypotenuse.

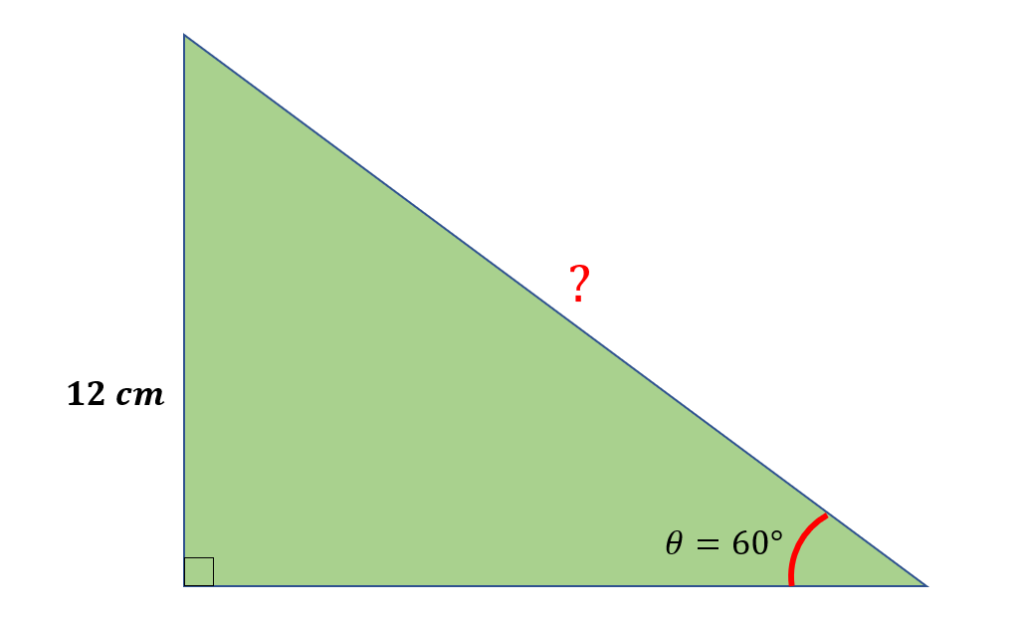
Solution

We know the angle = 60°, and the opposite side has a length of 12 cm. Since we must find the hypotenuse length, we will use the formula sin θ=$\frac{opposite}{hypotenuse}$.

Hence, we have,

sin θ=$\frac{opposite}{hypotenuse}$

sin 60°=$\frac{12 cm}{hypotenuse}$

hypotenuse=$\frac{12 cm}{sinsin 60^0}$

hypotenuse=$\frac{12 cm}{\frac{\sqrt{3}}{2}}$

hypotenuse=8$\sqrt{3}$ cm

Therefore, the length of the hypotenuse is 8$\sqrt{3}$ cm.

The Sine and Cosine Rules

Finding the lengths of a triangle’s sides and all of its angles is necessary to solve it. The sine and cosine rules may be used in solving any triangles. The sine rule is used when a side and its opposite angle are known. We apply the cosine rule when we have either two sides and the included angle or three sides of a triangle.

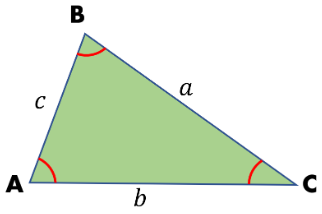side a is the opposite of ∠A side b is the opposite of ∠B side c is the opposite of ∠C

The Sine Rule

The sine rule may be used in solving any triangle, not just a right triangle. The sine rule is used when a side and its opposite angle are known.

$\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$ =$\frac{c}{sinsin C}$

$\frac{sinsin A}{a}$=$\frac{sinsin B}{b}$ = $\frac{sinsin C}{c}$

Note that we will only use two parts of the formula, not three parts.

Calculating Sides

In calculating the length of a side, the Sine Rule to use is where the side lengths are the numerators.

$\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$ =$\frac{c}{sinsin C}$

Example

Find the length of a in the figure below. 

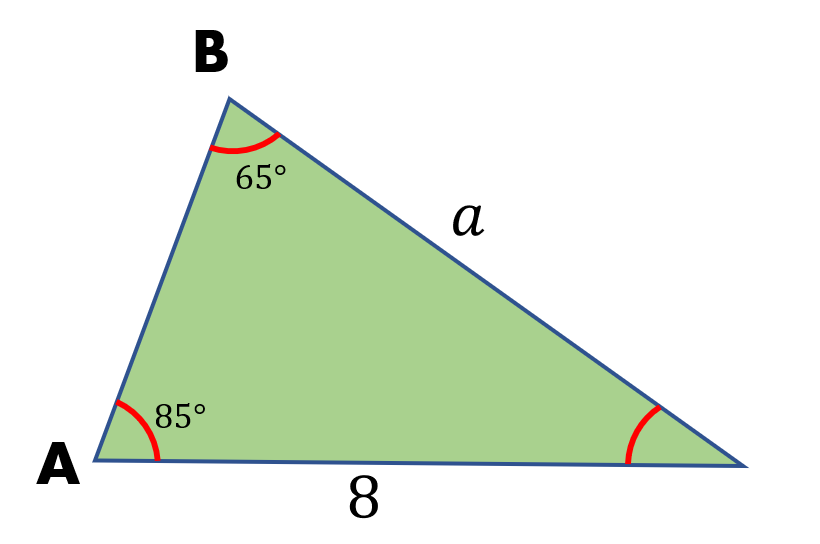
Solution

In the given figure, we know two angles, A and B, and a side, a. We will use the formula,

$\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$

Let us now substitute the known values and find the length of side a.

$\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$

$\frac{a}{sinsin 85^0}$ =$\frac{b}{sinsin 65^0}$

a=$\frac{8}{sin 65^0}$ x sin 85°

a≈8.79

Calculating Angles

In calculating the angle measures of a triangle, the Sine Rule to use is where the angle measures are the numerators.

$\frac{A}{sinsin a}$ =$\frac{B}{sinsin b}$ =$\frac{C}{sinsin c}$

Example

Find the missing angle in the figure below.

Solution

Since we know that ∠C = 70°, c = 11, and b = 9, we will use the sine rule,

$\frac{B}{sinsin b}$ =$\frac{C}{sinsin c}$

To find the missing ∠B, let us substitute the known values to the formula

$\frac{B}{sinsin b}$ =$\frac{C}{sinsin c}$

$\frac{B}{sinsin 9}$ =$\frac{70^0}{sinsin 11}$

sinsin B =$\frac{sinsin 70^0}{11}$ x 9

sin B=0.769   ( 3 decimal places)
Use the inverse function ( sin^-1 ) to find angle B.
∠B=0.769
∠B≈50.26° ( 2 decimal places )
Therefore, ∠B measures 50.26°.

The Cosine Rule

The cosine rule can be used in triangles where you try to relate all three sides to an angle. The following are the formulas to consider:

a²=b²+c² – 2bc coscos A

coscos A=$\frac{b^2+c^2-a^2}{2bc}$

where side a is the missing angle
sides b and c are the known angles
∠A is the angle opposite side a

Calculating Sides

Knowing the length of the other 2 sides and the measurement of the angle opposite the missing side are necessary to calculate the length of a triangle’s missing side. In this scenario, we will use the formula,

a²=b²+c² – 2bc coscos A

Remember that a is the missing side, b and c are the lengths of the other two sides, and ∠A is the angle opposite side a.

Example

Calculate the length of the missing side.

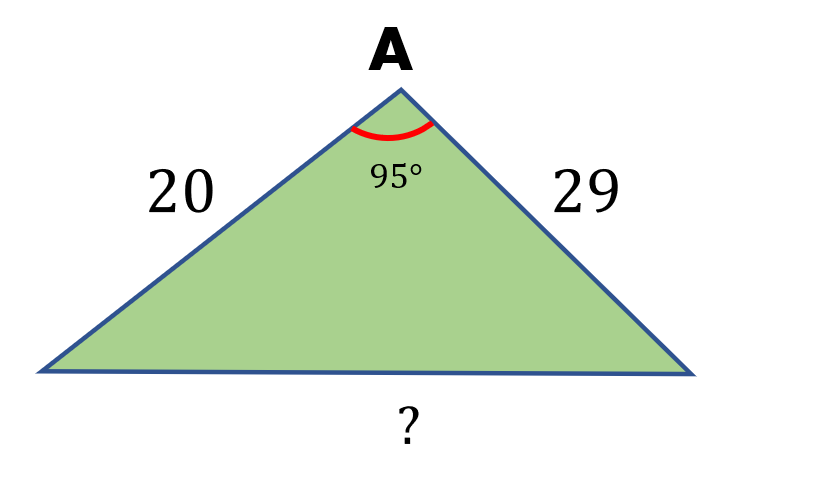
Solution

The given figure has the information: ∠A=95°, b=20, c=29. Let us now substitute the known values in the formula to find the missing side a.

a²=b²+c² – 2bc coscos A

a²=20²+29² – 2(20)(29)(coscos 95°)

a²=1342.100662
a=$\sqrt{1342.100662}$
a≈36.63

Therefore, the missing side-length measures 36.63 units.

Calculating Angles

To calculate the measure of an angle, we will use the formula,

cos A=$\frac{b^2+c^2-a^2}{2bc}$

Remember that ∠A is the missing angle, b and c are the lengths of the other two sides, and a is the side opposite ∠A.

Example

Calculate the measure of ∠A in the figure below.

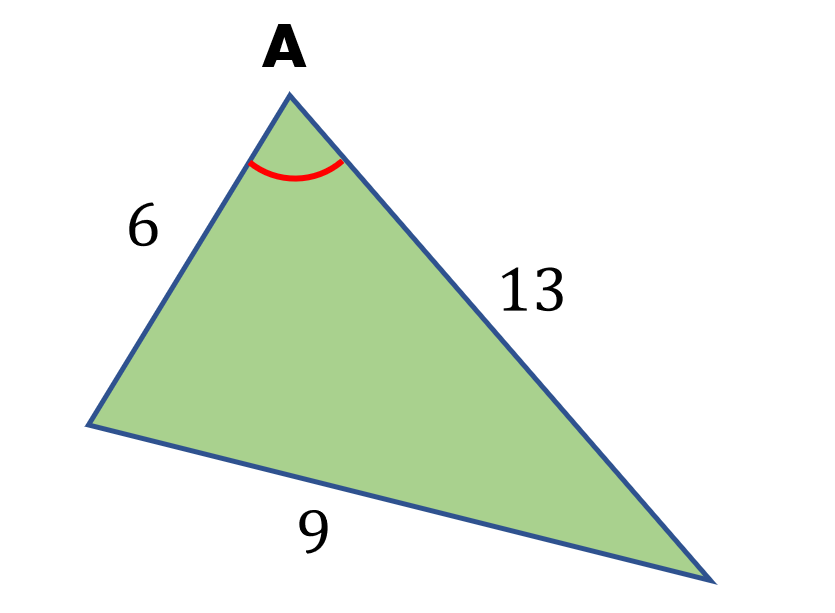
Solution

In the given figure, we are asked to find the measure of ∠A given the three sides of the triangle with measures 6, 9, and 13 units. The side opposite ∠A is the side with a measure of 9 units, so we must use it as side a. 

Let us use the formula below to calculate ∠A.

cos A=$\frac{b^2+c^2-a^2}{2bc}$

Substituting the known values to the formula, we have, 

cos A=$\frac{b^2+c^2-a^2}{2bc}$

cos A=$\frac{6^2+13^2-9^2}{2x6x13}$

cos A=$\frac{124}{156}$

cos A≈0.795 ( 3 decimal places )
Use the inverse function ( cos^-1 ) to find angle A.
∠A=0.795
∠A≈37.34° ( 2 decimal places )

Therefore, the missing angle A measures 37.34° using the cosine rule.

List of Geometry Formulas Triangles

Name	Definition	Formula
The Perimeter of a Triangle	A triangle’s perimeter is equal to the sum of its sides.	Perimeter = x + y + z
Area of a Triangle	The region bounded by a triangle’s perimeter, or its three sides, is known as the triangle’s area.	Area of a Triangle = ½ × base × height Heron’s Formula Area=$\sqrt{S (S-a)(S-b)(S-c)}$ The formula S = $\frac{a+b+c}{2}$ gives the semi-perimeter S.
Pythagorean Theorem	The Pythagorean theorem, also known as Pythagoras’ theorem, states that at a right angle, the square on the hypotenuse (the side across from the right angle) equals the total of the squares on the two smaller sides.	a2+b2=c2
Basic Trigonometric Functions	Solving problems based on the angles and sides of a right triangle requires using basic trigonometric functions like sine, cosine, and tangent.	Mnemonic Device: SOH CAH TOA sinsin θ=$\frac{opposite}{hypotenuse}$ coscos θ=$\frac{adjacent}{hypotenuse}$ tantan θ=$\frac{opposite}{adjacent}$
The Sine Rule	The sine rule may be used in solving any triangle, not just a right triangle. The sine rule is used when a side and its opposite angle are known.	$\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$ =$\frac{c}{sinsin C}$ $\frac{A}{sinsin a}$ =$\frac{B}{sinsin b}$ =$\frac{C}{sinsin c}$
The Cosine Rule	Any triangle whose three sides must be related to an angle is subject to the cosine rule.	a2=b2+c2-2bc coscos A coscos A=$\frac{b^2+c^2-a^2}{2bc}$ where side a is the missing angle sides b and c are the known angles∠A is the angle opposite side a

Summary

Triangles are polygons with three (3) sides and (3) interior angles. It is denoted by the symbol △. 

The list of fundamental formulas for working with triangles is displayed in the table below.

Geometry Formulas Triangles

The Perimeter of a Triangle

A triangle’s perimeter is equal to the sum of its sides.

Perimeter = x + y + z

Area of a Triangle

The region bounded by a triangle’s perimeter, or its three sides, is known as the triangle’s area.

Base and height are known

It is determined by taking the product of the triangle’s base and height and dividing it by two. It is always measured in square units. 

Area of a Triangle = ½ × base × height

Heron’s Formula

Given is Heron’s formula for calculating the area of a scalene triangle.

Area=$\sqrt{S (S-a)(S-b)(S-c)}$
where the variable S is the semi-perimeter.
The formula S = $\frac{a+b+c}{2}$ gives the semi-perimeter S.

Pythagorean Theorem

The Pythagorean theorem, also known as Pythagoras’ theorem, states that at a right angle, the square on the hypotenuse (the side across from the right angle) equals the total of the squares on the two smaller sides.

a²+b²=c²

where side c is the hypotenuse, and the other two legs of the right triangle are a and b.

Basic Trigonometric Functions

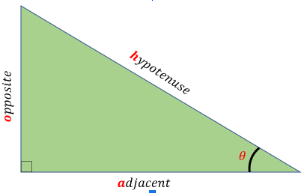
∟ used to represent the right angle of the triangle
θ (theta) is used to represent one of the angles in the right triangle but not the right angle
o is used to represent the opposite side  of the angle θ
a is used to represent the adjacent side of the angle θ
h is used to represent the hypotenuse of the right triangle
The mnemonic device for the three basic trigonometric functions is SOH CAH TOA.

sinsin θ=$\frac{opposite}{hypotenuse}$

coscos θ=$\frac{adjacent}{hypotenuse}$

tantan θ=$\frac{opposite}{adjacent}$

The Sine and Cosine Rules

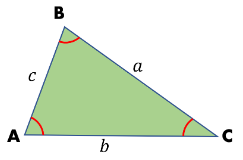
side a is the opposite of ∠A
side b is the opposite of ∠B
side c is the opposite of ∠C

Sine Rule $\frac{a}{sinsin A}$ =$\frac{b}{sinsin B}$ =$\frac{c}{sinsin C}$ $\frac{sinsin A}{a}$=$\frac{sinsin B}{b}$=$\frac{sinsin C}{c}$

Cosine Rule a2=b2+c2 – 2bc coscos A coscos A=$\frac{b^2+c^2-a^2}{2bc}$

Frequently Asked Questions on Geometry Formulas Triangles

What are the different types of triangles?

Triangles are classified by their sides and angles. Triangles can be categorized as scalene, isosceles, or equilateral based on the lengths of their sides. Triangles can be acute, obtuse, or right, depending on their angles. 

Types of Triangles by their Sides

Equilateral Triangle An equilateral triangle has three equal-length sides.

Isosceles Triangle Two of the sides of an isosceles triangle are of identical length.

Scalene Triangle A scalene triangle has no equal sides.

Types of Triangles by their Angles

Acute Triangle Angles in an acute triangle are all less than 90 degrees.

Right Triangle One side of a right triangle is 90 degrees in angle.

Obtuse Triangle An obtuse triangle has an angle that is higher than 90 degrees.

How do you calculate the area of a triangle?

The following formula is used to calculate a triangle’s area:

Area of a Triangle=1/2×base×height

What formula is used to determine the right triangle’s missing side?

The Pythagorean theorem, also known as Pythagoras’ theorem, states that at a right angle, the square on the hypotenuse (the side across from the right angle) equals the total of the squares on the two smaller sides. Hence, we use the formula,

a²+b²=c²

where side c is the hypotenuse, and the other two legs of the right triangle are a and b.

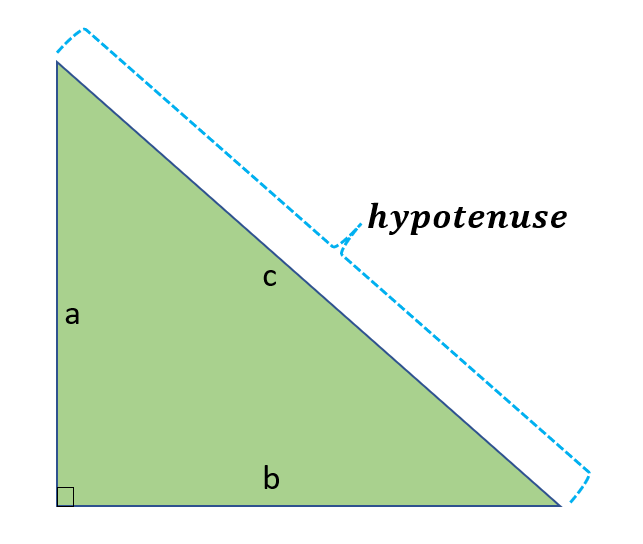
Using the Pythagorean Theorem, the right triangle’s side lengths (a, b, and c) can be calculated using the following formulas.

c=$\sqrt{a^2+b^2}$

a=$\sqrt{c^2-b^2}$

b=$\sqrt{c^2-a^2}$

Let us assume that the other two sides are 6 and 8 units in length and that we need to determine the length of the hypotenuse. The answer is:

c=$\sqrt{a^2+b^2}$

c=$\sqrt{6^2+8^2}$

c=$\sqrt{36+64}$

c=$\sqrt{100}$

c=10

What ae Pythagorean Triples?

Pythagorean triples, represented as ( a, b, c ), is a set of three positive integers that can be the sides of a right triangle. A Pythagorean triple satisfies the Pythagorean theorem equation a² + b² = c², 

Examples of Pythagorean Triples are as follows:

( 3, 4, 5 )	( 6, 8, 10 )	( 9, 12, 15 )	( 12, 16, 20 )	( 15, 20, 25 )
( 5, 12, 13 )	( 10, 24, 26 )	( 15, 36, 39 )	( 20, 48, 52 )	( 25, 60, 65 )
( 7, 24, 25 )	( 14, 48, 50 )	( 21, 72, 75 )	( 28, 96, 100 )	( 35, 120, 125 )
( 8, 15, 17 )	( 16, 225, 289)	( 24, 45, 51 )	( 32, 60, 68 )	( 40, 75, 85 )
( 9, 40, 41 )	( 18, 80, 82 )	( 27, 120, 123 )	( 36, 160, 164 )	(45, 200, 205 )

Recommended Worksheets

Triangles (Fashion Themed) Worksheets
Area of Triangles (Ice cream Themed) Worksheets
Spatial Skills: Triangles and Quadrilaterals (Winter Solstice Themed) Math Worksheets