Introduction
Imagine you’re holding a hula hoop. Take a string and tape its ends anywhere inside the hula hoop. That string represents a chord of the circle! The longest chord you could make would stretch from one side of the hula hoop to the other, passing through the center. That’s the diameter of the circle.
In this article, we will focus on
Grade Appropriateness
Depending on the school’s curriculum, the idea of a chord in a circle is typically introduced in either the 6th or 7th grade. At this point, students begin studying the chord and other parts of circles. It’s a fundamental idea that is a foundation for comprehending more complex geometric ideas.
Math Domain
The chord of a circle falls under the larger mathematical domain known as ‘Geometry‘. That deals with shapes, sizes, properties of space, and the relationships between different forms.
Applicable Common Core Standards
The study of the chord of a circle aligns with the following Common Core Standards:
7.G.B.4: Know the formulas for the area and circumference of a circle and use them to solve problems.
7.G.B.5: Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure.
Definition of the Topic
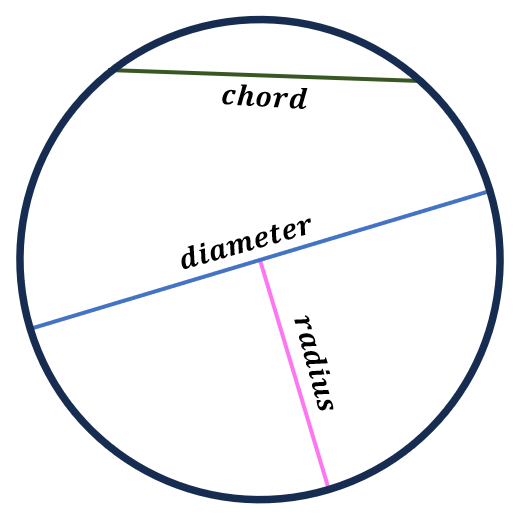
A chord of a circle is a line segment whose endpoints lie on the circle. It’s like a bridge across a river, but in this case, the river is the interior of the circle, and the endpoints of the bridge are on the circle.
Key Concepts
Here are some essential things to remember about chords:
The line segment joining any two points on the circle is a chord.
The longest possible chord of a circle is its diameter.
Perpendicular bisectors of a chord always pass through the center of the circle.
Chord Length formulas:
Chord Length=2×$\sqrt{r^2-d^2}$
Chord Length=2r×sinsin ($\frac{θ}{2}$)
Discussion with Illustrative Examples
The line segment joining any two points on a circle’s circumference is known as the chord of a circle.
The longest chord of a circle passes through the center of the circle. This chord is what we know as the diameter.
In the figure below, $\overline{PQ}$, $\overline{RS}$, and $\overline{TU}$ are chords of the circle. Chord RS is the diameter of the circle.
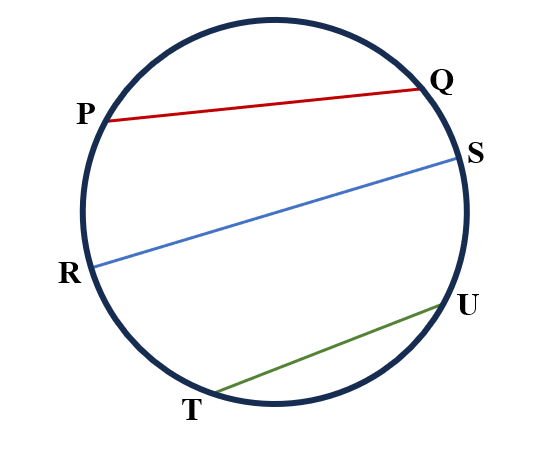
Properties of a Chord
| Properties of a Chord | Illustration |
| The chord is divided in half by a perpendicular drawn from the circle’s center. | 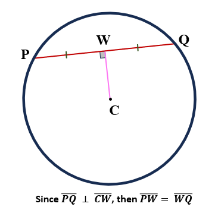 |
| The perpendicular bisector of a diameter is the radius of a circle. | 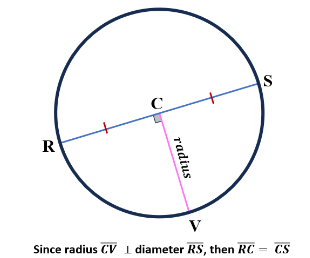 |
| A chord, when extended infinitely on both sides, becomes a secant. | 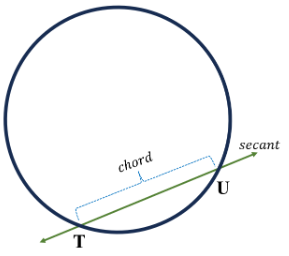 |
| As the perpendicular distance from the circle’s center to the chord decreases and vice versa, a chord’s length increases. | 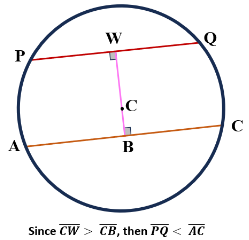 |
| A circle is split into two sections by its chord: the major portion and the minor segment. The circle is divided into two halves and is known as a semicircle if the chord is a diameter. | 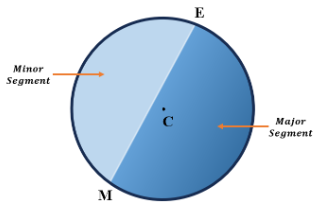 |
| An isosceles triangle is created by the radii connecting a chord’s ends to the circle’s center. | 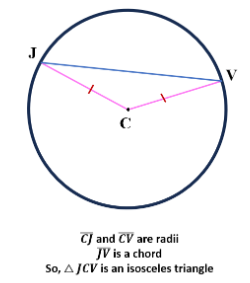 |
| If two chords have equal distances from the center of a circle | 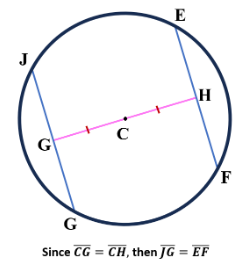 |
Chord of a Circle Theorems
The following are the theorems related to the chords of a circle.
| Theorem 1 A line perpendicular to a chord drawn from the center bisects the chord. |  |
| Theorem 2 Equal-in-length chords subtend equal angles at the center of the circle. |  |
| Theorem 3 If two chords are situated equally apart from the circle’s center, they have the same length. | 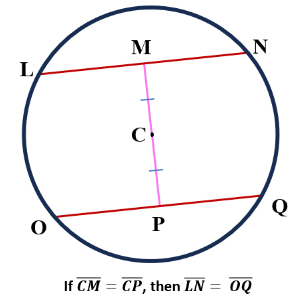 |
Finding the Length of a Chord
There are two ways to get the length of a chord of a circle. Which one to use? Well, you have to decide depending on what values you are given!
Chord Length Using the Perpendicular Distance from the Center
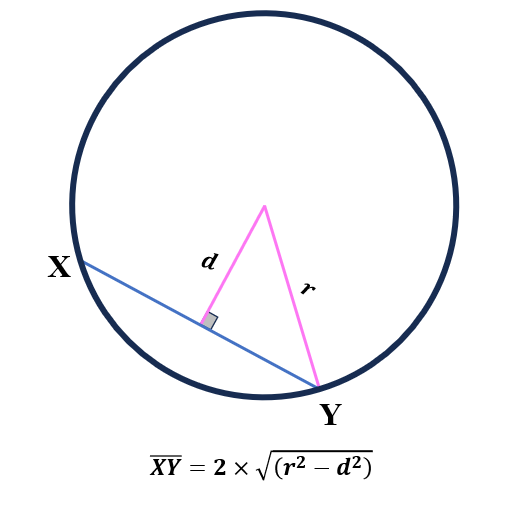
In finding the length of a chord when the radius and distance to the center of a circle are known, we use the formula,
Chord Length=2×$\sqrt{r^2-d^2}$
where d is the perpendicular distance from the center of a circle to the chord and r is the radius of the circle and
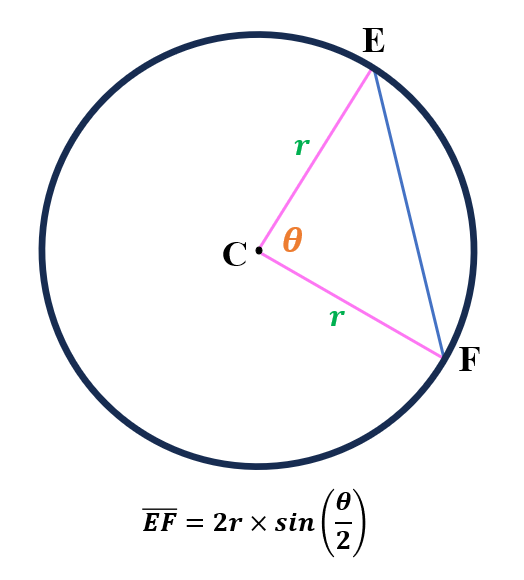
Chord Length Using Trigonometry
In finding the length of a chord given the radius and central angle, we use the formula,
Chord Length=2r×sinsin ($\frac{θ}{2}$)
where r is the radius, and is the angle subtended at the center by the chord.
Examples with Solution
Example 1
In the figure below, identify the chords in circle P.
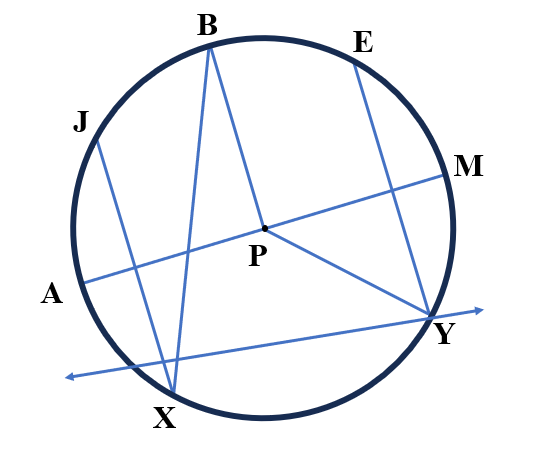
Solution
$\overline{JX}$, $\overline{BX}$, $\overline{EY}$, and $\overline{AM}$ are the chords in circle P.
Example 2
Find the chord length in each circle.
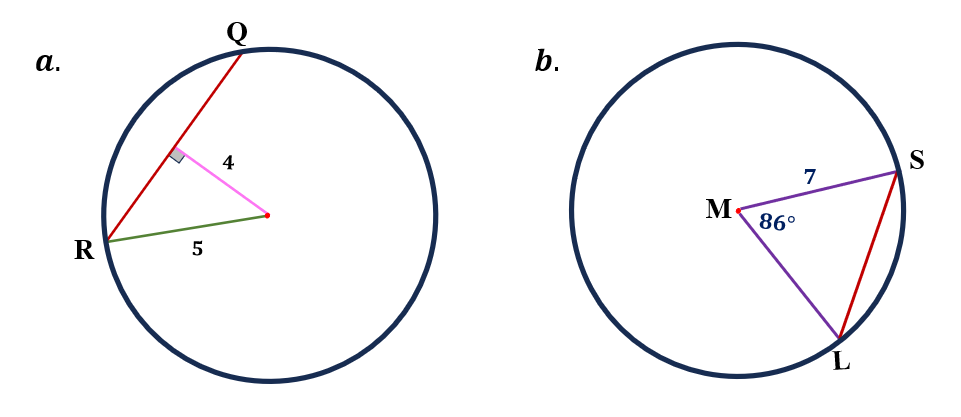
Solution
a. We must substitute the given r=5 and the perpendicular distance d=4 into the formula Chord Length=2×$\sqrt{r^2-d^2}$. So, we have,
QR=2×$\sqrt{5^2-4^2}$
QR=2×$\sqrt{25-16}$
QR=2×$\sqrt{9}$
QR=2×3
QR=6
Therefore, the length of chord $\overline{QR}$ is 6 units.
a. Substituting the given r=7 and central angle θ=86° into the formula Chord Length=2r×$\frac{sinsin θ}{2}$, we shall have,
$\overline{SL}$=2(7)sinsin ($\frac{86°}{2}$)
$\overline{SL}$=14×0.68
$\overline{SL}$=9.55
Hence, the length of chord $\overline{SL}$ is 9.55 units.
Example 3
The perpendicular distance of a chord from the center of the circle is 20 cm. Find the length of a chord if the circle’s diameter measures 58 cm.
Solution
The perpendicular distance d=20 cm while r=58 cm2=29 cm. Note that the radius of a circle is half the measure of its diameter.
Since we know that Chord Length=2×$\sqrt{r^2-d^2}$, we have,
Chord Length=2×$\sqrt{29^2-20^2}$
Chord Length=2×$\sqrt{(841-400)}$
Chord Length=2×21
Chord Length=42
Hence, the length of the given chord is 42 cm.
Example 4
The length of a chord is 48 inches, and its perpendicular distance from the center of the circle is 45 inches. Find the radius of the circle.
Solution
What we have is the perpendicular distance, d, which is 45 inches and the chord length of 48 inches. By the formula we have,
2×$\sqrt{r^2-45^2}$=48 (Substitution)
4(r2-2025)=2304 (Square both sides)
r2-2025=576 (Divide both sides by 4)
r2=576+2025 (Add 2025 on both sides)
$\sqrt{r^2}$=$\sqrt{2601}$
r2=2601 (Square root of both sides)
r=51
Therefore, the radius of the circle is 51 inch
Real-life Application with Solution
Problem 1
Suppose you are constructing a circular garden with a 10-meter diameter. You want to create a straight-across walkway, but you want it to be 2 meters from the center. What is the length of that walkway (chord)?
Solution
The radius of your garden is 5 meters (half of 10 meters), and the distance from the center to the walkway is 2 meters. Let us substitute r=5 and d=2 into the formula to find the length of the walkway.
Length of the Walkway Chord=2×$\sqrt{5^2-2^2}$
Length of the Walkway Chord=2×$\sqrt{25-4}$
Length of the Walkway Chord=2×$\sqrt{21}$
Length of the Walkway Chord≈9.17
Thus, the full length of the walkway is 2$\sqrt{21}$ meters or approximately 9.17 meters.
Practice Test
1. What is the longest chord a circle with a 6 cm radius may have?
2. A chord of a circle is 8 cm long and is 3 cm away from the center. What is the radius of the circle?
3. A circle has a diameter of 12 inches. If a chord is 5 inches away from the center, how long is the chord?
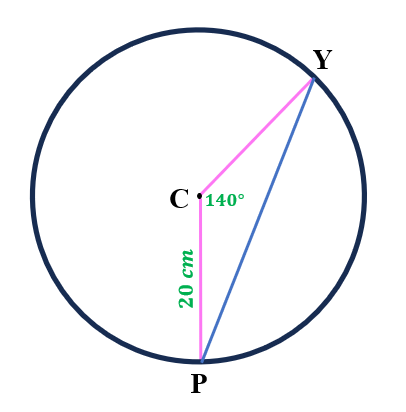
4. Calculate the length of chord PY.
Answers
1. The longest chord of a circle is its diameter, so if its radius is 6 cm, then its longest chord is 12 cm.
Diameter=2r
Diameter=2×6 cm
Diameter=12 cm
2. Chord Length=2×$\sqrt{r^2-d^2}$.
8=2×$\sqrt{r^2-3^2}$
8=2×$\sqrt{r^2-9}$
64=4$\sqrt{r^2-9}$
16=r2-9
16+9=r2
25=r2
5=r
The radius of the circle is 5 centimeters.
3. r=6; d=5
Chord Length=2×$\sqrt{r^2-d^2}$
Chord Length=2×$\sqrt{(6^2-5^2)}$
Chord Length=2×$\sqrt{36-25}$
Chord Length=2$\sqrt{11}$
Chord Length≈6.63 inches
4. By the formula, we have,
$\overline{PY}$=2(20)x sinsin $\frac{140°}{2}$
$\overline{PY}$=40×0.94
$\overline{PY}$=37.59
Hence, the length of chord PY is 37.59 cm.
Frequently Asked Questions (FAQs)
1. What’s the difference between a chord and a radius?
A radius is a line segment from the circle’s centre to any point on the circle, while a chord is a line segment whose endpoints lie on the circle. The diameter is a particular chord that passes through the circle’s centre.
2. Can the chord of a circle ever be outside the circle?
No. A chord is always within the circle, as its endpoints must be on the circle.
3. Is the diameter of a circle also a chord?
Yes, the diameter is a particular type of chord – it is the longest possible chord because it passes through the circle’s centre.
4. Is every line that passes through the center of a circle a diameter?
Every line segment whose endpoints are on the circle and that passes the circle’s center is a diameter.
5. How can the concept of a chord be useful in real life?
Understanding chords can be helpful in various fields, including engineering, architecture, and computer graphics. For instance, designing a round table with evenly spaced seats requires knowledge of chords.
6. What formulas are used for calculating the length of a chord of a circle?
In finding the length of a chord when the radius and distance to the center of a circle are known, we use the formula,
Chord Length=2×$\sqrt{r^2-d^2}$
In finding the length of a chord given the radius and central angle, we use the formula,
Chord Length=2r×sinsin $\frac{θ}{2}$
where r is the radius, and is the angle subtended at the center by the chord.
Recommended Worksheets
Chord (National Pizza Day Themed) Math Worksheets
Central Angle of a Circle (Fast Food Themed) Math Worksheets
Arcs of a Circle (National Donut Day Themed) Math Worksheets









