Introduction
The lateral area of a hemisphere is an essential mathematical concept that students learn to grasp and apply in various scenarios. This comprehensive article seeks to provide an in-depth understanding of the topic, its key concepts, and real-life applications. We will explore the topic’s grade appropriateness, related math domain, Common Core Standards, and practical examples to help students and educators.
Grade Appropriateness
The concept of the lateral area of a hemisphere is typically introduced in middle school, around the 7th or 8th grade, and extends into high school geometry and pre-calculus courses.
Math Domain
The lateral area of a hemisphere belongs to the domain of geometry, a branch of mathematics that deals with shapes, sizes, and properties of figures.
Applicable Common Core Standards
The relevant Common Core Standards for studying the lateral area of a hemisphere are:
7.G.B.4: Know the formulas for the area and circumference of a circle and use them to solve problems.
8.G.C.9: Know the formulas for the volumes of cones, cylinders, and spheres, and use them to solve real-world problems.
G.GMD.A.1: Give an informal argument for the formulas for the circumference of a circle, the area of a circle, the volume of a cylinder, a pyramid, and a cone.
Definition of the Topic
The lateral area of a hemisphere refers to the curved surface area of a hemisphere, which is half of a sphere. It does not include the flat circular base.
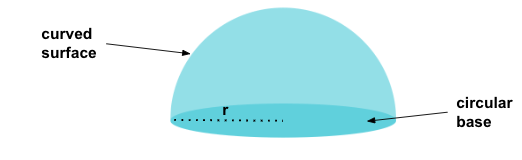
Key Concepts
Hemisphere
A hemisphere is half of a sphere divided along a great circle, usually referred to as the equator.
Lateral area
The lateral area is the curved surface area of a solid, excluding its bases.
Discussion with Illustrative Examples
Surface Area is the total area covering the surface or outside part of a three-dimensional object. The formula 4πr2 is used to determine the surface area of a sphere, so half of that is the curved surface area of a hemisphere.
The word hemisphere has the prefix hemi, which came from the Greek term hēmi meaning “half.” So, the hemisphere means half of a sphere.
To get the lateral area of a hemisphere (L), we simply use the formula:
L = 2πr2
where:
r is the radius of the hemisphere.
π (pi) is approximately equal to 3.14159.
Remember that the lateral surface area of a hemisphere does not include the area of the circular base. If we add the area of the base to the lateral surface area, we will get the total surface area.
Examples with Solution
Example 1
Calculate the lateral area of a hemisphere with a radius of 5 cm.
Solution
L = 2πr2
L =(2)(3.14159)(52)
L ≈ 157.08 cm2
Therefore, the lateral area of the hemisphere is 157.08 cm2.
Remember always to write the unit of measurement on your final answers! For surface areas, the answers should be in square units.
Example 2
Find the lateral surface area of a hemisphere with a radius of 7 cm.
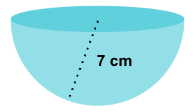
Solution
L= 2πr2
L=(2)(3.14159)(72)
L≈ 307.88 cm2
Therefore, the lateral surface area is 307.88 cm2.
Example 3
Determine the lateral surface area of a hemisphere whose diameter is 51 cm.
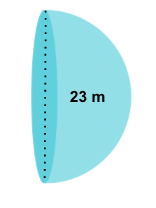
Solution
The radius of the hemisphere is 23÷2 = 11.5 m since the radius is equal to half of the diameter.
L = 2πr2
L =(2)(3.14159)(11.52)
L ≈ 850.95 m2
Therefore, the lateral surface area is 850.95 m2.
Real-life Application with Solution
Example 1
A hemispherical dome with a radius of 10 meters needs to be painted. Work out how many square meters of paint will be required to cover the curved surface area.
Solution
L = 2πr2
L =(2)(3.14159)(102)
L ≈ 628.32 m2
The painter will require 628.32 square meters of paint to cover the curved surface area of the dome.
Example 2
What is the lateral surface area of the coconut cut into a hemisphere with a diameter of 6 inches used by a stall selling coconut juice?

Solution
Since the diameter of the coconut is 6 inches, its radius is 3 inches. Calculating the lateral surface of its hemisphere, we have,
L = 2πr2
L =(2)(3.14159)(32)
L ≈ 56.55 in2
The lateral surface of the coconut cut into a hemisphere is 56.55 square inches.
Practice Test
A. Complete the table below. Round off your answers to the nearest hundredths.

B. Answer the following problem.
1. Calculate the lateral area of a hemisphere with a radius of 7 cm.
2. Find the lateral area of a hemisphere with a diameter of 12 meters.
3. A hemispherical container has a radius of 4 meters. How much material is needed to create a cover for the curved surface area?
4. What is the lateral area of a hemisphere with a circumference of 18.85 cm?
5. A hemisphere has a lateral area of 100 cm2. Find the radius of the hemisphere.
Frequently Asked Questions (FAQs)
What is the formula for a hemisphere’s lateral area?
The formula for a hemisphere’s lateral area is Lateral Area = 2πr2, where r is the radius of the hemisphere.
How does the lateral area of a hemisphere differ from the total surface area?
The lateral area of a hemisphere refers only to the curved surface area, whereas the total surface area includes both the curved surface and the flat circular base.
Can the lateral area of a hemisphere be equal to the total surface area?
No, the lateral area of a hemisphere cannot be equal to the total surface area, as the total surface area includes the curved surface and the flat circular base, making it larger than the lateral area.
How does a hemisphere’s lateral area compare to a sphere’s surface area?
The lateral area of a hemisphere is exactly half the surface area of a sphere with the same radius since a hemisphere is half of a sphere.
Is there a relationship between a hemisphere’s volume and lateral area?
There is no direct relationship between a hemisphere’s volume and lateral area. However, both can be calculated using the hemisphere’s radius. The volume formula is $\frac{2}{3}$r3, and the lateral area formula is 2πr2.
Recommended Worksheets
Lateral Area of a Hemisphere (Rio Carnival Themed) Math Worksheets
Surface Area of a Hemisphere (Halloween themed) Math Worksheets
Lateral Surface Area of a Sphere (Commonwealth Day Themed) Math Worksheets









