Introduction
In Algebra, an inequality is a mathematical expression that uses the inequality symbol to indicate the relationship between two statements. Both sides of an inequality sign have different expressions. It signifies that the left-hand side expression should be more than or less than the right hand side expression, or vice versa. Literal inequalities are when the relationship between these two algebraic expressions is defined using inequality symbols.”An inequality exists when two real numbers or algebraic expressions are connected by the symbols “>”, “”, .> “, For instance, x>3 (x should be greater than 3)
If there is only one variable in the inequality, it is called an open sentence or one variable inequality. One variable inequality may be a linear or higher order. Precisely for further discussion, we discuss one variable linear inequality or one variable quadratic inequality. So, first we define these one variable inequalities and then their solution method.
One variable linear inequality
Definition:
A linear inequality is a mathematical expression that compares two linear expressions and declares one to be bigger or less than the other. The linear equations in one variable are equations that are written as ax + b = 0, where a, and b are two integers and x is a variable, and there is only one solution. 8x + 3 = 8, for particular, is a linear equation with only one variable. As a result, there is only one solution to this equation, which is x = 97/2.Here are a few good examples of linear inequalities that are all addressed throughout this section:
Examples:-
- 3x > 6
- 8x + 6 < 4x
- 145x + 9>16 − 2x + 1
- 5x ≥ 1
- X < 6
These are one variable linear inequality with variable x. The power of x is one that’s why it is called linear inequality and due to one variable, they are linear one variable inequality.
Counter Examples
The counter examples of linear one variable inequality are as follows.
- 2x^4+5 < 3 it is one variable but not linear
- Y + 5X = 78
- X^2 – z = 7
- 2x + 14y > 234 and
- 3y + 4x + 3xy these are called inequalities two variables because here we used two variables x and y. so, it is also include in the counter example of linear one variable inequality.
Solution:
When a real number is replaced for the variable in a linear inequality, the result is a true assertion. Linear inequalities can have an unbounded number of solutions or none at all. If there are infinitely many possibilities, graph the set on a line segment and/or use interval notation to illustrate the answer.
To calculate a one-variable inequality, convert it to an expression (a mathematical phrase with a “=” sign) and solve it. On a number line, write the solution, often known as a “boundary point.” The number line is divided into two parts at this point. For circumstances involving or, the boundary point is included in the solution; for instances involving strictly > or, it is excluded. Boundary points that are included in the solutions are indicated on the number line as a solid filled-in circle, whereas excluded solutions are shown as an open circle. After then, pick a number from each zone split by the border point and see if it is true or untrue in the initial inequality. If this is the case, then any integer in that area is a solution to the inequality. If it’s false, then there’s no number within this region that can solve the inequality.
We have to follow some rules while solving one variable linear inequality.
Rules:-
Solving inequalities follows a similar set of criteria as solving mathematical equation. When multiplying or dividing by a negative number, there is one exception.
To eliminate an inequity, we can:
- To both sides, add the same number.
- Reduce the same amount from both sides of the equation.
- Both sides should be multiplied by the same positive value.
- Subtract the same positive value from both sides.
- Change the sign and multiply both sides by the same negative value.
- Change the sign and divide both sides by the same negative number.
For example
If we have
X + 5 > -2
If we multiply this inequality by -2 then we have
-2x – 10 < 4
Compare these, multiply by -2 changed the sign of inequality.
Now see some examples for solving one variable linear inequality
Hence, Inequalities can also be solved by dividing or multiplication both sides by a variable. To solve the inequality 5x > 3, for example, multiply both sides by 5 to get x > 35. When we multiply or divide by a negative integer, though, something unusual happens. For example, we know that 5 is greater than 3. However, if both sides of the inequality 5>3 are multiplied by -2, we get 10>6. We know this isn’t true because -10 is smaller than -6.
When we multiply or divide an inequality by a negative number, this occurs, and we must reverse the sign to make the inequality true. To multiply 2 > 4 by -3, for example, we multiply the 2 and 4 by -3 each, then alter the sign to a < sign, resulting in 6 < 12.
Examples:-
Example 1
Solve this equation: 6x – (x + 10) <0
We need separate the variable on one side of the inequality sign to resolve an inequality. We employ the same fundamental approaches used to solve the equation to isolate the factor. Most inequalities can be solved by adding or removing a constant from one side of the equation.
Convert the problem to an equation and solve it.
6x – x – 10 = 0
5 x – 10 = 0
5x = 10 this implies x = 10/5 so, x = 2
Hence we split the real line into two intervals
(-∞, 2 ) (2 , ∞)
Now we will pick one test point in each test interval and check the sign of inequality then decide solution includes which interval.
| Test interval | test point | sign of the inequality 5x – 10 |
| ( – ∞,2) | 5 | -25-10 <0 |
| ( 2,∞ ) | 5 | 25 – 10 > 0 |
Hence interval (-∞, 2) satisfies the solution region. So, this is the required solution.
On the number line, write the solution (boundary point).
Solution -2 -1 0 1 2
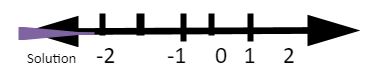
We use a filled-in dot since x = 2 is also a solution to the inequality (< ). In the initial inequality, test a number on either side of the boundary point. The section containing the data that make the inequality true should be highlighted.
Example 2
4x > 24 was the original problem.
Divide both sides by 4
4x / 4 > 24 / 4
x > 6
x > 6 is a simplified version of this inequality.
Example 3
The building of one house stands four storey’s higher than the another building. Find the number of stories in each building if the total number of stories in both buildings is 24.
Method
We know that x = number of stories of one building which is is higher than another and x + 8 = other building height.
(x + 8) + x = 24
2x + 8 = 24
2x = 24 – 8
2x = 16
x = 16/2
x = 8 hence, one building contains 8+8 is 16 stories and other is 8.
Hence, in one variable, most linear equations have precisely one solution. In at least one example , a linear equation may have an unlimited number of solutions, but in that case, every real integer is a solution. The “simple” inequality we’re looking at, x <2, has an endless number of solutions, but not every real integer is one of them. 3 is not a solution, for example: 3< 2 is false.
Quadratic inequality of one variable
Definition
The exponent of the highest power to which the variable is raised in an equation is the degree of that equation in one variable. Inside one variable, the second degree equation is one in which the variable is increased to the power of two. A QUADRATIC EQUATION is a term that describes a second-degree equation. The word quadratic comes from the Latin similar assets, which means literally “square.” The squared term is the highest degree term in a quadratic equation. For instance, consider quadratic equations the form of the quadratic equation ax^2+bc+c > 0 or ax^2 +bx + c <0
The terms with a lower degree than the second may or may not exist. The first-degree term and the constant term are lower-degree terms in a quadratic equation than the squared term. In the formula
Solution methods
We can solve the inequality algebraically as well as graphically
When solving a quadratic inequality, we must first determine the set of alternatives, or intervals, whereby the inequality holds. This is much more complicated than the linear example and may include more than one unique period. The steps outlined below can be used to solve quadratic inequalities.
Solving a Quadratic Inequality:
A Step-by-Step Guide Algebraically
Reorganize the inequality so that most of the expression’s parts, expressed as f ( x ), are on one side, with just an inequality connecting them to zero. For instance, f ( x ) 0 r f (x ) > 0. To determine the solutions to the equation, solve f ( x ) = 0 via factoring or otherwise. Choose test points for every interval such that values just under, between, and greater than the equation’s solutions are represented. A sign chart can also be used to determine whether the intervals will be positively or negatively. Determine which intervals meet the inequality.
Summary of steps:
We can also summarize these steps in to the following
- Use this action to solve a quadratic inequality:
- As though it were an equation, solve the inequality.
- The genuine solutions to the equation serve as boundary points for the inequality’s formulation.
- If the original inequality contains equality, make the border points solid circles; otherwise, make them open circles.
- Choose points from each of the boundary point-created zones. In the initial inequality, replace these “test points” with these “test points.”
- When a test point meets the original inequality, the region in which it is located is part of the solution.
- Show the solution graphically and in the form of a solution set.
Example
Solve the problem (x – 3)(x + 2) > 0
Write its inequality in the form of equation
(x – 3)(x + 2) = 0 (x – 3)(x + 2) = 0 (x – 3)(x + As a result of the zero product property, equation
Make the line of demarcation. So because original inequality did not involve equality, the dividing line points are open circles.
Choose points from the several regions that have been developed equation.
Examine the test points to see if they satisfy the initial inequality.
(x – 3)(x + 2) = 0
This implies (x – 3) = 0 or (x + 2 ) = 0
X = 3 or x = -2
The testes intervals are
(-∞,-2) and -2 , 3 , ( 3 , ∞)
Now, we check the signs in each tested interval of the inequality
| Tested intervals | Test point | (x – 3)(x + 2) sign |
| ( -∞,-2) | -5 | ( – 5 – 3)(-5 +2) >0Positive |
| (-2 , 3) | 0 | (0 – 3)(0 + 2) <0 Negative sign |
| (3, ∞) | 5 | (5 -3)(5 +2)>0Positive |
Hence the nested intervals (-∞, -2) and (3,∞) satisfy the inequality condition. So, their union is the required solution set of the inequality.
We were able to follow the technique for solving a quadratic inequality perfectly in the first example by first resolving the quadratic and then utilizing a symbol chart, but this is not always desirable or necessary. We’ll look at a quadratic inequality that can’t be factored in the next example.
Example
To solve the inequality x^2+121 0, find all possible solutions. Write your response as a series of intervals.
There would be no need to rearrange this inequality because it was supplied to us with all terms on one side of the equation. Normally, we would try to solve f(x)= 0.where f(x)=x^2+121 to start looking for solutions. However, there are no solutions to this problem because x will always be bigger than zero for any real value of x. To put it another way, x^2+121>0 , As a result, the inequality’s left-hand side is always strictly bigger than zero, implying that x+1210 is never true.
This can be demonstrated graphically by noting that the graph of f(x)=x^2+121 don’t ever crosses the x-axis, as illustrated below. The solution is the empty set written as an interval.
As a result our answer for this inequality is empty set.
We solved quadratic inequalities with the right side of the inequality equal to zero in the previous two examples. While both sides of an inequality have nonzero expressions, the inequality must first be simplified to the point where first side becomes zero.
Hence we conclude
An interval or a union of intervals is the solution to a quadratic inequality. We could use set difference terminology to write it as the complement of one interval when it is a union of two intervals.
The steps of solving a quadratic inequality algebraically are as follows: f(x) > 0
Rearrange the inequality so that all of the expression’s terms are on one side, for example, using an inequality connecting this to zero. F(x) = 0
Factor the inequality by determining the expression’s roots. F(x)
Using test points in each interval or a sign chart, find the intervals that meet the inequality. A graph of the function can also be drawn.
Follow the instructions below to solve a quadratic inequality graphically.
Rearrange the inequality so that all of the expression’s terms are on one side, and an inequality connects them to zero; for example.
To find the expression’s roots, factor the inequality by setting.
Using the equation’s roots, draw the graph of the equation and determine the direction of the parabola curve. If you’ve altered the initial inequality to change the sign of the x value, be especially cautious: Instead of using the original inequality, use the x coefficient in the rearranged form of the inequality to determine the curve’s shape.
Determine which intervals satisfy the inequality.
Key points
Hence, in general
- A one-variable linear inequality has an infinite number of solutions. As a result, the answers are usually represented by a graph on a number line.
- A typical graph of a linear inequality is half of a number line, with all points to the left or right of the border value, and the shaded region showing inequality solutions.
- In the event of a strict inequality (or >), the border value is indicated by an open circle (), while in the case of a non-strict inequality (or), the border value is indicated by a solid circle (•).
- The test value method or the standard form approach can be used to determine which side of the border value to shade.









