Parabola

Introduction

A conic section as the name implies is a section cut off from a circular ( not necessarily a right circular ) cone by a plane in various ways. The shape of the section depends upon the position of the cutting plane. In other words conic section or conic is the locus of a point P which moves in such a way that its distance from a fixed point S always bears a constant ratio to its distance from a fixed line, all being in the same plane. 

One such important conic is the parabola. Let us learn more about it.

Definition 

Parabola is the locus of a point that moves in a plane such that its distance from a fixed point in the plane is always equal to its distance from the fixed straight line in the same plane. The fixed point is called the focus of the parabola, and the fixed line is called the directrix of the parabola. The key features of a parabola are its vertex, axis of symmetry, focus, directrix, and focal diameter. When given a standard equation for a parabola centred at the origin, we can easily identify the key features to graph the parabola.

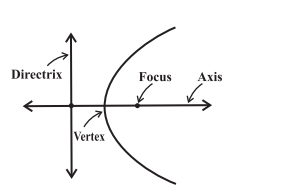
Here are some important terms that are integral to parabola – 

Focus – The fixed point is called the focus of the parabola. In general every parabola has four foci, where two of them are real while the other two are imaginary. Due to the presence of these two real foci, every parabola has two directrices that correspond to each real focus.

Directrix – The fixed straight line is called the directrix of the parabola.

Eccentricity – The constant ratio is called the electricity of the parabola and is denoted by e

Axis – The straight line passing through the focus and perpendicular to the directrix is called the axis of the parabola.

Vertex – The points of intersection of the parabola and the axes are called vertices of the conic section.

Centre – The point which bisects every chord of the parabola passing through it is called the centre of the conic.

Latus-Rectum – The latus-rectum of a parabola is a chord passing through the focus and perpendicular to the axis.

Equation of a Parabola in its Standard Form

The equation of the parabola is the simplest when the vertex of a parabola is at the ‘origin’ and the axis of symmetry is along the x or y-axis. Let us derive the equation of a parabola in its standard form.

Let S be the focus and Z, Z’ be the directrix of a parabola. Raw SK perpendicular from S on the directrix and bisect SK at A.  

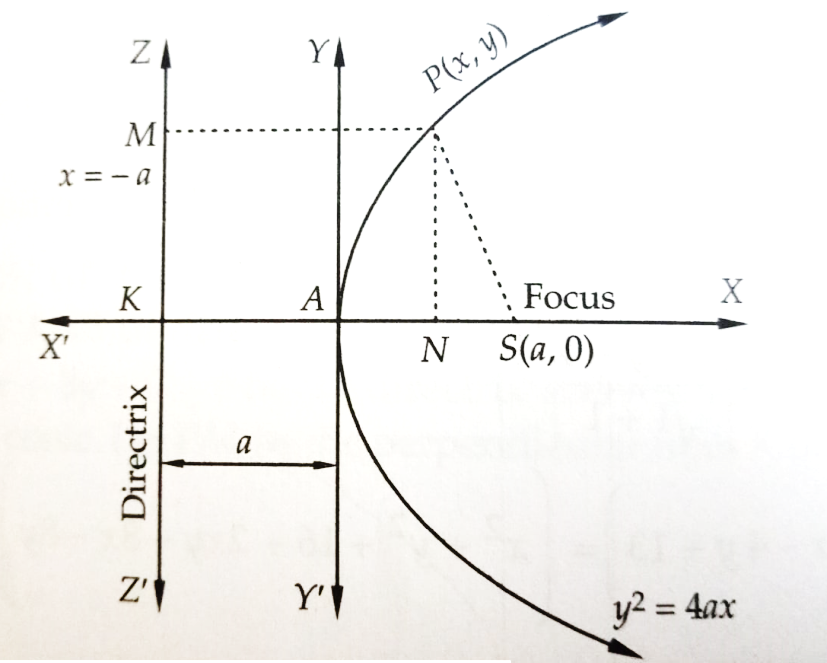
We then have,

AS = AK

⇒ Distance of A from the focus = Distance of A from the directrix.

⇒ A lies on the parabola

Let S  = 2a. Then, AS = AK = a

Let us choose A as the origin, AS as the x-axis and AY a perpendicular to A as y-axis. Then the coordinates of S are ( a, 0 ) and the equation of the directrix ZZ’ is x = – a.

Let P (x, y ) be any point on the parabola.. Join SP and draw PM and PN perpendiculars on the directrix ZZ’ and X-axis. Then we have,

PM =  NK = AN + AK = x + a

Since P lies on the parabola, therefore,

SP = PM

⇒ SP² = PM²

⇒ ( x + a )² + ( y – 0 )² = ( x + a )²

 ⇒ y² = 4ax 

Hence, the equation of a parabola in its standard form is y² = 4ax

Other Standard Forms of a Parabola

It is important to note that other than the above standard form, there exist three other standard forms of a parabola. These three forms are – 

y² = – 4ax

x² = 4ay

x² = – 4ay

The forms depend on the choice of axis.  It is important to note that the four standard forms are based on the axis and the orientation of the parabola. The transverse axis and the conjugate axis of each of these parabolas are different. 

Important Points pertaining to the Standard Forms of a Parabola

1. The parabola is symmetric with respect to its axis. This means that the axis of symmetry of a parabola is along the x-axis if the equation has the term with y ^2. On the other hand an equation of a parabola has the axis of symmetry along the y-axis if the equation has the term with x ².
2. The parabola opens to the right if the coefficient of the x is positive and the axis of symmetry is along the x-axis. However, if the coefficient of x is negative the parabola opens to the left.
3. The parabola opens upwards if the axis of symmetry is along the y axis and the coefficient of wire is positive. On the other hand if the coefficient of Y is negative the parabola will open downwards. 

The following table shows different values of the four standard forms of a parabola – 

	y2 = 4ax	y2 = – 4ax	x2 = 4ay	x2 = – 4ay
Coordinates of Vertex	( 0, 0 )	( 0, 0 )	( 0, 0 )	( 0, 0 )
Coordinates of Focus	( a, 0 )	( – a, 0 )	( 0, a )	( 0, – a )
Equation of the Directrix	x = – a	x =  a	y = – a	y = a
Equation of the axis	y = 0	y = 0	x = 0	x = 0
Length of the Latus Rectum	4 a	4 a	4 a	4 a
Focal Distance	a + x	a – x	a + y	a – y

Graph of a Parabola

The given equation of a parabola can be written as y = ± 2 $\sqrt{ax}$. The following points can be observed clearly – 

For every positive value of x, there are two equal and opposite values of y.

For every negative value of x, the value of y is imaginary. Therefore, no part of the curve lies to the left of the y-axis.

The curve passes through the origin and the tangent at the origin is x = 0, i.e. y-axis.

The curve meets the coordinate axis only at the origin.

As x → ∞ , y → ∞. Therefore, the curve extends to infinity to the right of the axis of y. 

Based on the above points, the general graph of the four forms of parabola is as below – 

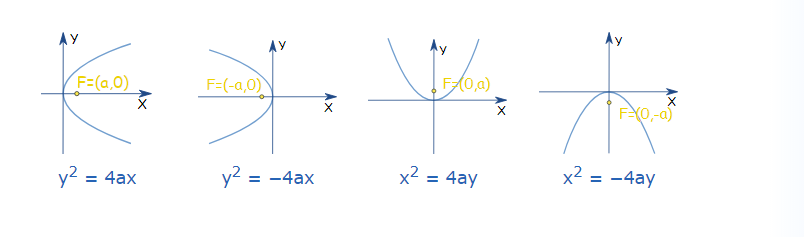
Examples

Example 1 Find the vertex, axis, focus, directrix, latus rectum of the parabola; also draw a graph of the parabola 4y² + 12x – 20y + 67 = 0

Solution We have been given the parabola 4y² + 12x – 20y + 67 = 0 and we need to find its vertex, axis, focus, directrix and latus rectum. Let us find them one by one.

The given equation is

4 y² + 12 x – 20 y + 67 = 0

⇒ y² + 3 x – 5 y + $\frac{67}{4}$ = 0

⇒ y²  – 5 y  = – 3 x –  $\frac{67}{4}$

⇒ y²  – 5 y + ( $\frac{5}{2}$)2 = – 3 x –  $\frac{67}{4}$ + ( $\frac{5}{2}$)²

⇒ ( y –  $\frac{5}{2}$)² = – 3 x –  $\frac{42}{4}$

⇒ ( y –  $\frac{5}{2}$)² = – 3 ( x + $\frac{7}{2}$ ) …………………….. ( 1 )

Shifting the origin to the point ( -$\frac{7}{2}$, $\frac{5}{2}$ ) without rotating the axis and denoting the new coordinates with respect to these axis by X and Y we have,

x = X – $\frac{7}{2}$ and y = Y + $\frac{5}{2}$ …………………….. ( 2 )

Substituting these values in the equation ( 1 ) we have,

Y² = – 3 X     ……………………….. ( 3 )

This is of the form Y² = – 4 a X

On comparing we have, 4 a = 3 ⇒ a = $\frac{3}{4}$

Now, that we have the value of a, let us find out the vertex, axis, focus, directrix and latus rectum of the parabola.

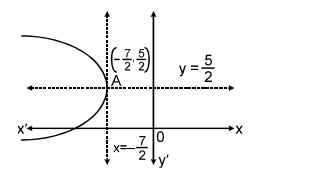
Vertex – The coordinates with respect to the new axis are ( X = 0, Y = 0 ). 

We shall now substitute X = 0 and Y = 0 in equation ( 2 ). 

So, the coordinates of the vertex with respect to the old axis are ( -$\frac{7}{2}$, $\frac{5}{2}$ )

Hence, the vertex of the parabola is ( -$\frac{7}{2}$, $\frac{5}{2}$ )

Axis – The equation of the axis of the parabola with respect to the new axis is Y = 0. 

We shall now substitute Y = 0 in equation ( 2 )

So, the equation of the axis with respect to the old axis is y = $\frac{5}{2}$

Hence, the axis of the parabola is y = $\frac{5}{2}$

Focus – The coordinates of the focus with respect to the new axis are  ( X = – a , Y = 0 ) i.e. ( X = – $\frac{3}{4}$ , Y = 0 ). 

We shall now substitute X = – $\frac{3}{4}$ and Y = 0 in equation ( 2 )

So, the coordinates of the focus with respect to the old axis are (  – $\frac{17}{4}$,  $\frac{5}{2}$)

Hence, the focus of the parabola is (  – $\frac{17}{4}$,  $\frac{5}{2}$)

Latus Rectum –  The length of the latus rectum of the given parabola is 4 a = 3

The graph of the parabola will be – 

Example 2 Find the equation of the parabola with vertex ( 2, – 3 ) and focus ( 0, 5 ).

Solution In order to find the equation of a parabola we need to know the coordinates of its focus and the equation of the directrix. We are given the coordinates of its focus and the vertex. So we need to find the equation of the directrix.

Let Z ( x₁, y₁ ) be the point of intersection of axis and the directrix. The vertex A is the midpoint of the line segment joining the focus S and the point Z that of intersection of the axis and the directrix. Therefore ( 2, – 3 ) is the midpoint of the line segment joining S ( 0 , 5 )  and Z ( x₁, y₁ ).

Therefore, we have,

$\frac{x_{1}+0}{2} = 2$ and $\frac{y_{1}+5}{2} = – 3$

x₁ = 4 and y₁ = – 11

Thus we can now say that the directrix meets the axis at Z ( 4,  – 11 )

Now, let m₁ be the slope of the AS. Then we have,

m₁ = $\frac{5+3}{0-2}$ = – 4

Now, let m₂ be the slope of the directrix. Since, directrix is perpendicular to AS, therefore, we have,

m₁ m₂ = – 1

m₂  = – $\frac{1}{m_1} = \frac{1}{4}$

This the directrix passes through the point Z (4, – 11 ) and has slope $\frac{1}{4}$. Therefore, the equation of the directrix will be –

$y + 11 = \frac{1}{4} ( x – 4 ) or x – 4 y – 48 = 0$

Let  P ( x , y ) be any mid point on the required parabola and let PM be the length of the perpendicular from P on the directrix. Then,

SP = PM

SP² = PM²

$(x -a )^2 + ( y – 5 )^2 = \left |\frac{x-4\:y-48}{\sqrt{1^2-(-4)^2}} \right |^2$

17 x ²  + 17 y ² – 170 y + 425 = x ² + 16 y ² + 2304 – 8  x y – 96 x + 384 y

16 x ²  + y ² + 8 x  y  + 96 x  – 554 y – 1879 = 0 which is the required equation of the parabola.

Example 3 Find the equation of the parabola whose co-ordinates of vertex and focus are ( – 2, 3 ) and ( 1, 3 ) respectively.

Solution We have been given that co-ordinates of vertex and focus of a parabola are are ( – 2, 3 ) and ( 1, 3 ) respectively. This implies that since the ordinates of vertex and focus are equal hence, the axis of the required parabola is parallel to x-axis. Therefore, we have 

a =  abscissa of focus – abscissa of vertex

⇒ a = 1 – ( – 2 ) = 1 + 2 = 3

Therefore, the equation of the required parabola is

  ( y – β ) ² = 4 a (x – α)                 

⇒ ( y – 3 ) ² = 4 x 3 ( x + 2 )

⇒ y ² – 6 y + 9 = 12 x + 24

      ⇒ y ² – 6 y – 12 x = 15

Hence, the equation of the parabola whose co-ordinates of vertex and focus are ( – 2, 3 ) and ( 1, 3 ) respectively i y ² – 6 y – 12 x = 15

Key Facts and Summary

1. A conic section or conic is the locus of a point P which moves in such a way that its distance from a fixed point S always bears a constant ratio to its distance from a fixed line, all being in the same plane.
2. The fixed point is called the focus of the parabola. In general every parabola has four foci, where two of them are real while the other two are imaginary. Due to the presence of these two real foci, every parabola has two directrices that correspond to each real focus.
3. The fixed straight line is called the directrix of the parabola.
4. The constant ratio is called the electricity of the parabola and is denoted by e
5. The straight line passing through the focus and perpendicular to the directrix is called the axis of the parabola.
6. The points of intersection of the parabola and the axes are called vertices of the conic section.
7. The point which bisects every chord of the parabola passing through it is called the centre of the conic.
8. The latus-rectum of a parabola is a chord passing through the focus and perpendicular to the axis.
9. Parabola is the locus of a point which moves in a plane such that its distance from a fixed point in the plane is always equal to its distance from the fix straight line in the same plane.
10. The equation of a parabola in its standard form is y² = 4ax
11. The parabola is symmetric with respect to its axis. This means that the axis of symmetry of a parabola is along the x-axis if the equation has the term with y ^2. On the other hand an equation of a parabola has the axis of symmetry along the y-axis if the equation has the term with x ².
12. The parabola opens to the right if the coefficient of the x is positive and the axis of symmetry is along the x-axis. However, if the coefficient of x is negative the parabola opens to the left.
13. The parabola opens upwards if the axis of symmetry is along the y axis and the coefficient of wire is positive. On the other hand if the coefficient of Y is negative the parabola will open downwards.