Simultaneous equations are two equations, each with the same two unknowns and are “simultaneous” because they are solved together.
Worksheets
Click below for the Simultaneous Equations Worksheet Generator which provides limitless questions for practice.
In simple terms, the solution to a pair of simultaneous equations is the x and y values of the coordinates of the point at which the graphs cross or intersect. The example below shows this.
Solving Graphically
For each equation, find coordinates for two points on the graph. An easy way of doing this is finding corresponding values when x = 0 and when y = 0. (Note: this will give 2 sets of coordinates which, since the equation is linear, is enough although it is a god idea to check at least one more point on the line.)
For 4x – 2y = 10 this gives (2.5, 0) and (0,-5) which we plot and then extend a straight line through.
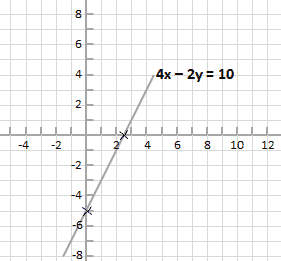
For x + y = 4 this gives (0,4) and (4,0) which we plot and then extend a straight line through.

Notice that the all the coordinates through which the lines pass are solutions to each equation. And the coordinates of the point at which they cross, (3,1)is the solution to the pair of simultaneous equations.
Solving Algebraically
We can find solutions to simultaneous equations algebraically too. There are two common methods. Which one you choose might depend on the values involved or it might just be the method you like the most. We will use the same pair of equations as above.
Elimination Method
| 4x – 2y = 10 x + y = 4 |
Multiply x + y = 4 by 2 to give 2x + 2y = 8 |
| 4x – 2y = 10 2x + 2y = 8 6x = 18 x = 3 |
We then add the two equations which “eliminates” the 2y (since -2y + 2y = 0) and leaves 6x = 18 which, after dividing both sides by 6 leaves x = 3 |
| 3 + y = 4 y = 1 |
We can then replace x in one of the equations with the value 3. (in this example, doing this in x + y =4 is simpler than in 4x – 2y = 10) |
| 4x – 2y = 10 (4 x 3) – (2 x 1) = 10 12 – 2 = 10 |
It is always a good idea to check the values for x and y in the other equation.
Substitution Method
| 4x – 2y = 10 x + y = 4 |
Rearrange one equation to get make either x or y subject of the equation. In this case it will be simpler to rearrange x + y = 4 which we can rearrange to y = 4 -x by subtracting x from each side |
| 4x – 2y = 10 4x – 2(4 – x) = 10 4x – 8 + 2x = 10 6x – 8 (+8) = 10 (+8) 6x = 18 x = 3 |
We then substitute 4 – x for y in the other equation. |
| 3 + y = 4 y = 1 |
As with the elimination method we then replace x in one of the equations with the value 3. (in this example, doing this in x + y =4 is simpler than in 4x – 2y = 10) |
| 4x – 2y = 10 (4 x 3) – (2 x 1) = 10 12 – 2 = 10 |
And, as a check, try the values for x and y in the other equation.
More Examples Using Algebraic Methods
There is one example of each the elimination and substitution methods for solving simultaneous equations shown below.
Elimination Method
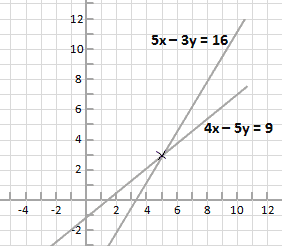
Substitution Method
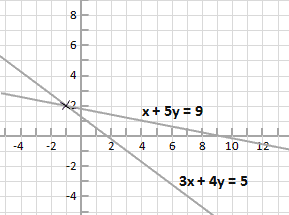
Simultaneous Equations in Real-life
Sam and Jack have $50 between them and Sam has $5 more than Jack. How much money does each have?
s + j = 50
s – j = 5
s = 27.50 , j = 22.50
This example is quite simple – you might be able to work it out by trial-and-error – but you can use any of the methods above to solve it.
And finally,…
Remember to practice with questions from the Simultaneous Equations Worksheet Generator.









