WHAT IS INEQUALITY?
Inequality is a relationship between two numbers or algebraic expression which is not equal. Inequalities can sometimes be presented as either question which can be solved or a statement of fact in the form of theorems. There are four inequality terms we can use to compare two quantities namely, greater than, greater than or equal to, less than, and less than or equal to.
HISTORY OF INEQUALITY SYMBOLS
Inequality as a mathematical concept is not a foreign concept to ancient mathematicians (Bagni, 2005) as they already knew the triangle inequality as a geometric fact and the arithmetic-geometric mean inequality (Fink, 2000). However, in 1631, the symbols for greater than and less than in the book “Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas” or The Analytical Arts Applied to Solving Algebraic Equations by Thomas Harriot was first introduced. Harriot, a British mathematician died in 1621 and his book was published 10 years after his death. Pierre Bouguer, a French mathematician put a line under the inequality symbols to represent greater than or equal to and less than or equal to. The symbols < and > was then introduced in 1734.
GREATER THAN
Greater than is one of the inequalities used when a quantity is larger or bigger than the other quantity or quantities. The figure below shows the symbol used to denote greater than.
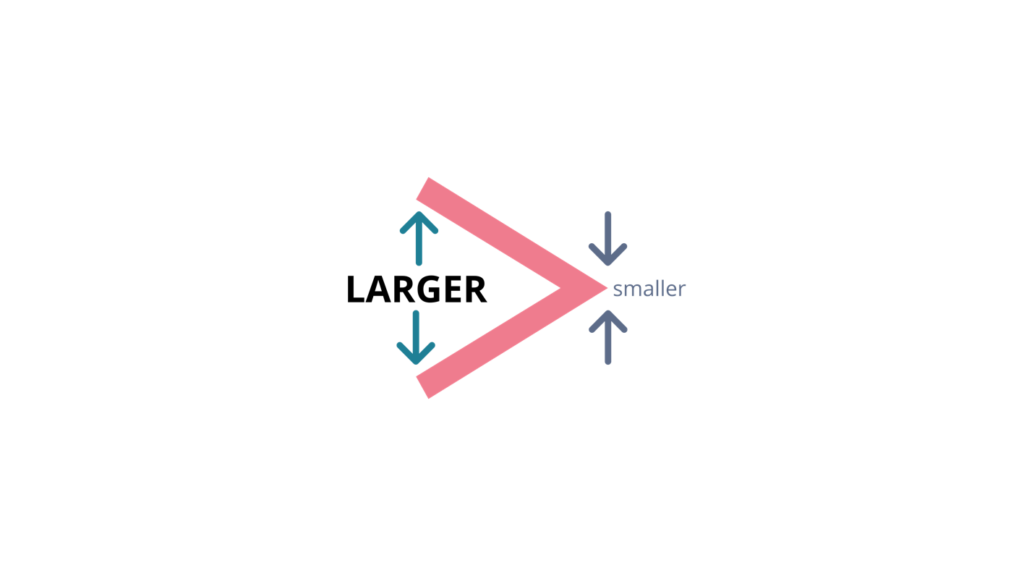
The notation a > b means a is larger than b. For example, 2 > 1.
Observe the given figure below. Just by looking, it can easily be noted that the left side have flowers than the right side. Therefore, we can say that 7 flowers is greater than 4 flowers.

Another example is comparing the value of money.

In the left side, we have a total value of $110 while on the right side we have a total value of $70. Therefore, we can say that $110 > $70.
GREATER THAN OR EQUAL TO
Greater than or equal to is a term that is used to show relationship in linear inequalities. Greater than or equal assumes that the value of a variable can be equal to or greater than a certain number. Using the terms at least can also mean greater than or equal to. As shown in the figure below, the difference between the “greater than” and “greater than or equal to” symbol is the additional line below the greater than symbol.
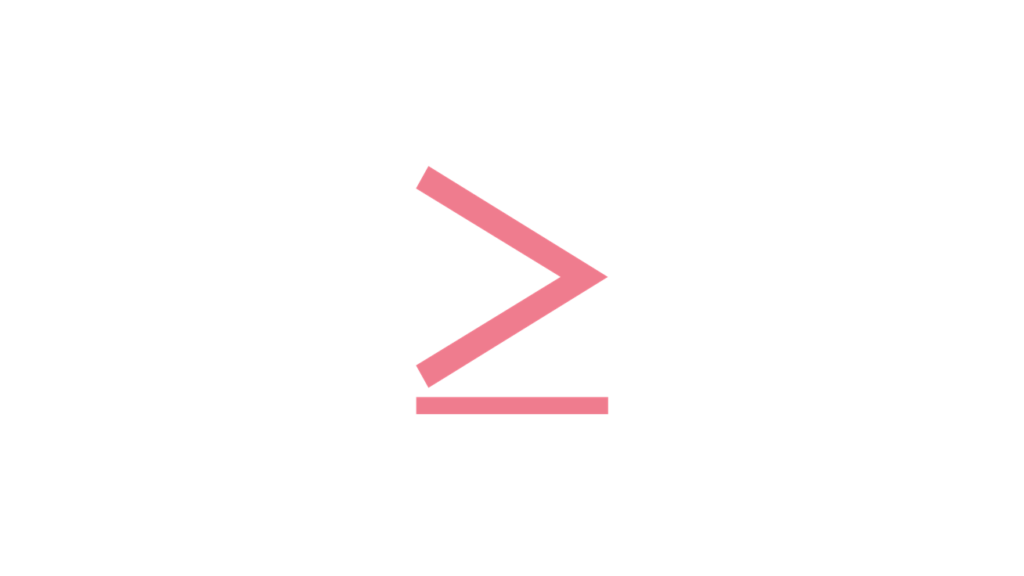
The table below shows how we can use the symbol greater than or equal to and how we will define it.
| EXAMPLE | MEANING |
| $x\geq 7$ | The inequality means that the value of x can be equal to 7 or any number greater than 7 such as 8, 20, etc. |
| $-1\geq x\geq3$ | For this example, it means that the value of can be equal to 3 or -1, or any number between -1 and 3 such as 0 and 1. Therefore, we can say that the value of x is inclusive between -1 and 3. |
LESS THAN
When the first value stated is smaller than the second value, we use the term less than. Less than is used to show the relationship between a smaller and larger value. The symbol used to represent less than is shown in the figure below.
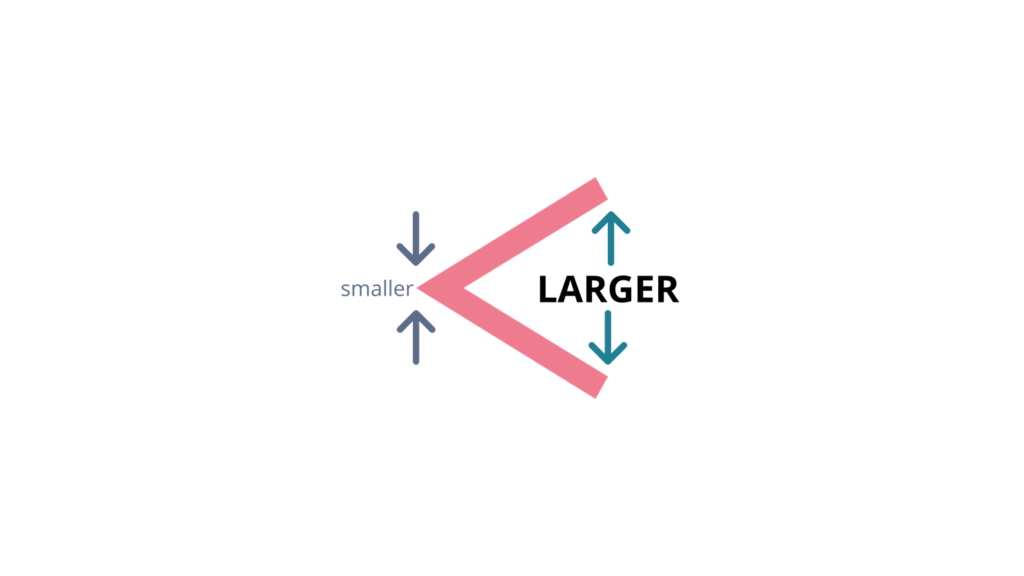
The notation a < b means a is smaller than b. For example, 1 < 2.
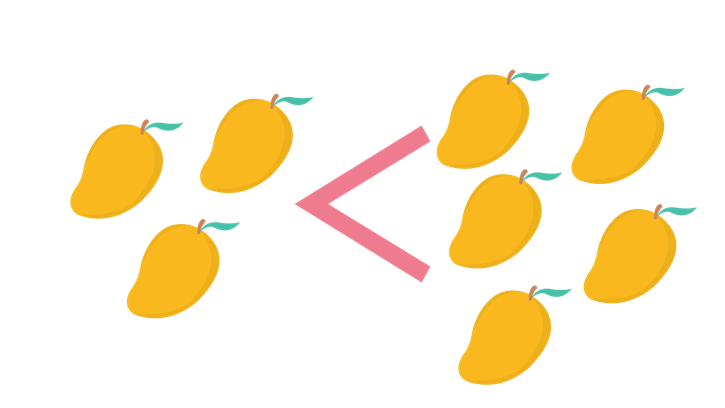
Take another example below. We can clearly see that the left side have less mangoes than of those in the right. So, we can say that 3 mangoes is less than 5 mangoes.
LESS THAN OR EQUAL TO
As the name suggests, less than or equal to means that a variable is either less than or equal to the other number, expression, or term. Using the terms “at most”, “no more than”, “maximum of”, and “not exceeding” also means less than or equal to. Shown in the figure below is the symbol used to express less than or equal to. You can notice the line below the “less than” symbol that makes it different from each other.
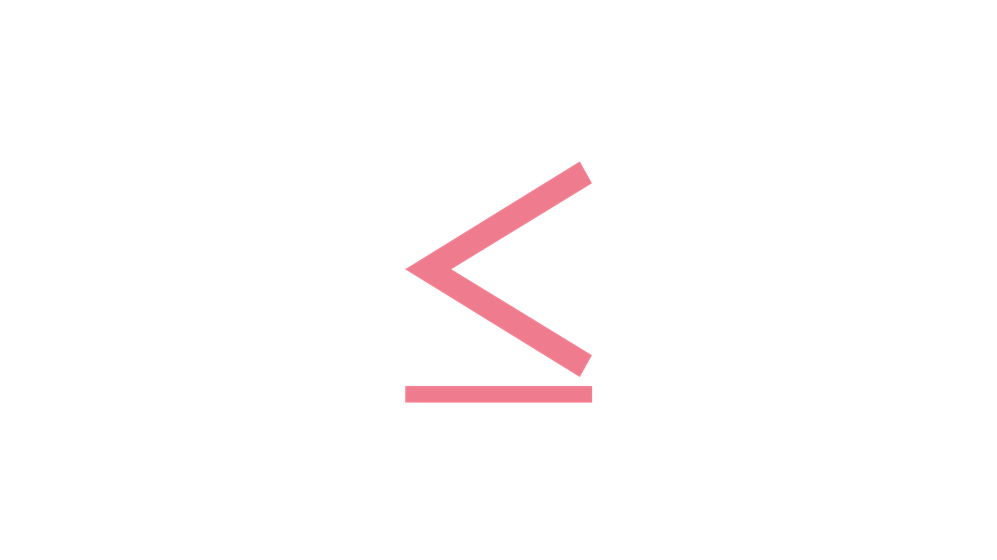
The table below shows how we can use the symbol greater than or equal to and how we will define it.
| EXAMPLE | MEANING |
| $x\leq 1$ | The value of x can be equal to 1 or any number less than 1 such as 0, -1, -5, etc. This inequality also means that the largest possible number for x is 1. |
| $-4\leq x\leq 4$ | This inequality means the value of x should lie between -4 and 4 such as -2, 0, and 1, inclusive of -4 and 4. |
USING INEQUALITY IN COMPARING NUMBERS
When comparing numbers, we use the symbols > and < to show their relationships with each other. Always take note that the wider mouth points to the larger number.
EXAMPLE #1
What inequality symbol will show the relationship between 35__21?
Since 35 is larger than 21, we will use >. Therefore, 35 > 21.
EXAMPLE #2
Observe the figure below and determine the appropriate inequality symbol.

Looking at the photo, we can say that the right-hand side has more ice cream than the left-hand side. Therefore, we will use < since 2 ice creams is less than 4 ice creams.
PROPERTIES OF INEQUALITY
LAW OF TRICHOTOMY
The law of trichotomy for real lines states that for any real numbers a and b, only one of 𝑎 < 𝑏, 𝑎 = 𝑏, and 𝑎 > 𝑏 is true.
Suppose we have the statements, 8 < 9, 8 = 9, 8 > 9, only of it is true. Since we know that 9 is larger than 8, then we can say that the only true statement is 8 < 9.
CONVERSE PROPERTY
Converse property of inequality states that < and >, ≤ and ≥ are each other’s converse. Which means, for any real numbers a and b, 𝑎 < 𝑏 and 𝑏 > 𝑎 and 𝑎 ≤ 𝑏 and 𝑏 ≥ 𝑎 are equivalent, or we can simply say that:
𝑎 < 𝑏 ↔ 𝑏 > 𝑎
𝑎 ≤ 𝑏 ↔ 𝑏 ≥ 𝑎
Say for example we have 3 < 7. By converse property of inequality, 3 < 7 is the same as 7 > 3.
TRANSITIVE PROPERTY
For any real numbers a, b, and c,
- If 𝑎 < 𝑏 and 𝑏 < 𝑐, then 𝑎 < 𝑐.
- If 𝑎 > 𝑏 and 𝑏 > 𝑐, then 𝑎 > 𝑐.
Suppose 21 > 19 and 19 > 8, then by transitive property of inequality, 21 > 8.
ADDITION PROPERTY
In addition property of inequality, if a common constant term c is added to both sides of inequality then, for any real number a, b, and c:
- if 𝑎 < 𝑏, then 𝑎 + 𝑐 < 𝑏 + 𝑐.
- if 𝑎 ≤ 𝑏, then 𝑎 + 𝑐 ≤ 𝑏 + 𝑐.
For example,
If we add 19 in the inequality 13 > 9, using the addition property of inequality, it follows that:
13 + 19 > 9 + 19
32 > 28
SUBTRACTION PROPERTY
Subtraction property of inequality states that if a common constant term c is subtracted to both sides of inequality, then, for any real number a, b, and c:
- if 𝑎 < 𝑏, then 𝑎 − 𝑐 < 𝑏 − 𝑐
- if 𝑎 ≤ 𝑏, then 𝑎 − 𝑐 ≤ 𝑏 – 𝑐
For example, if we deduct 3 in the inequality 6 < 12, then by subtraction property of inequality, it follows that:
6 – 3 < 12 – 3
3 < 9
MULTIPLICATION PROPERTY
For any real numbers a, b, and $c\neq 0$,
- if 𝑎 < 𝑏 and 𝑐 > 0, then 𝑎𝑐 < 𝑏𝑐
- if 𝑎 < 𝑏 and 𝑐 < 0, then 𝑎𝑐 > 𝑏𝑐
- if 𝑎 ≤ 𝑏 and 𝑐 > 0, then 𝑎𝑐 ≤ 𝑏𝑐.
- If 𝑎 ≤ 𝑏 and 𝑐 < 0, then 𝑎𝑐 ≥ 𝑏𝑐.
Suppose the inequality 4 < 7 and 𝑐 = 9. By multiplication property of inequality,
4 × 9 < 7 × 9
36 < 63
Another example is when 1 < 3 and 𝑐 = −1. If we multiply -1 to the inequality 1 < 3, it follows that:
1 × -1 < 3 × -1
-1 > -3
Take note that every time you multiply an inequality with negative number, you must reverse the inequality symbol.
DIVISION PROPERTY
For any real numbers a, b, and $c\neq 0$,
- if 𝑎 < 𝑏 and 𝑐 > 0, then $\frac{a}{c}< \frac{b}{c}$
- if 𝑎 < 𝑏 and 𝑐 < 0, then $\frac{a}{c}> \frac{b}{c}$
Suppose 21 < 51 and 𝑐 = 3, then by division property of inequality,
$\frac{21}{3}< \frac{51}{3}$
$7 < 17$
Take another example, if we have an inequality 20 > 10 and 𝑐 = −5, then applying division property of inequality will result to:
$\frac{20}{-5}> \frac{10}{-5}$
$-4 < -2$
Remember, every time you divide a negative number to an inequality, the inequality symbol will reverse.
ADDITIVE INVERSE PROPERTY
The additive inverse property of inequality states that for any real numbers a and b,
if 𝑎 < 𝑏, then −𝑎 > −𝑏.
if 𝑎 ≤ 𝑏, then −𝑎 ≥ −𝑏.
MULTIPLICATIVE INVERSE PROPERTY
The multiplicative inverse property of inequality states that if for any real numbers a and b that are both positive or both negative,
- if a < b, then $\frac{1}{a}> \frac{1}{b}$.
- if a > b, then $\frac{a}{c}< \frac{b}{c}$.
INEQUALITY IN NUMBER LINE
GRAPHING GREATER THAN IN A NUMBER LINE
To graph the inequality greater than, use an open circle to mark the starting value and point the arrow towards the positive infinity. The figure below shows how you can easily spot an inequality that denotes greater than.

EXAMPLE
Graph x > 3.
SOLUTION
The graph below shows the when represented in a number line. You can see the open circle that is located above 3 as it extends to positive infinity.

To denote the solution set of the given inequality above, we use the symbols ( and ) to indicate that the endpoint of the line is not included. This symbol is used when you see a graph that is an open circle. Hence, we can denote the solution set of $x>3$ as $(3, +\infty )$.
GRAPHING GREATER THAN OR EQUAL TO IN A NUMBER LINE
To graph the inequality greater than or equal to, use a closed circle to mark the starting value and point the arrow towards the positive infinity or right side. The figure below shows how you can easily spot an inequality that denotes greater than or equal to.

EXAMPLE
Graph $x\geq 3$.
SOLUTION
To represent the graph of in a number line, start by putting a close circle on top of number 3 then extend the line towards the positive infinity. The figure below shows the graph for $x\geq 3$.

To write the solution set of $x\geq 3$ , use the symbols [ and ] to indicate that the endpoint/s of the line is/are also included. This symbol is used when you see a graph with endpoint/s that is/are a close circle. Thus, we can denote the solution set of $x\geq 3$ as [$ 3, +\infty $).
GRAPHING LESS THAN IN A NUMBER LINE
To graph less than inequality, use an open circle to mark the starting value and point the arrow towards the negative infinity or left side. The figure below shows how you can easily determine an inequality that denotes less than.

EXAMPLE
Graph $x<3$.
SOLUTION
To draw the graph for in a number line, use the open circle to denote the starting point which is 3. Then, extend the line towards negative infinity. The graph below represents the inequality $x<3$.

Representing the solution set of $x<3$ , will give us $(-\infty,3)$. Remember that when denoting the solution set, you must always start with the smallest possible value. Since the graph shows an open circle, we use the symbol ( and ) to represent its solution set.
GRAPHING LESS THAN OR EQUAL TO IN A NUMBER LINE
To graph less than or equal to inequality, use close circle to mark the starting value and point the arrow towards the negative infinity or left side. The figure below shows how you can easily determine an inequality that denotes less than or equal to.

EXAMPLE
Graph $x\leq 3$.
SOLUTION
To represent the graph of in a number line, draw a close circle to which the line will start. In this case, the value given is 3. Then, extend the line from 3 to negative infinity. The figure below shows the graph for $x\leq 3$.

To write the solution set of $x\leq 3$, we use the symbols [ and ] to indicate that the value of 3 is included. Thus, the solution set of $x\leq 3$ is ($-\infty,3$].
CHAINED NOTATION
When we see notations such as a ≤ b ≤ c or a ≤ b < c, it means we have a chained notation. If we break down the chained notation a ≤ b ≤ c, it means a ≤ b and b ≤ c. This notation describes a double inequality that have a lower and upper limit of the number b. By transitive property of inequality, it also follows that a ≤ c .
EXAMPLE #1
What is the solution set given -1 < x < 10?
SOLUTION
To denote the solution set of -1 < x < 10, we will start by determining the lowest and largest possible value x can have. In this inequality, -1 will be the lower limit and 10 being the upper limit. Since the inequality shows both notations using <, then we will use ( and ). Therefore, the solution set is (-1, 10).
EXAMPLE #2
What is the solution set given -4 < x ≤ 5 ?
SOLUTION
If we break down the chained notation, it will give us inequalities −4 < 𝑥 and 𝑥 ≤ 5. By converse property of inequality, −4 < 𝑥 is equivalent to 𝑥 > −4. Hence, we have 𝑥 > −4 and 𝑥 ≤ 5. Then, we can say that -4 is the lower limit and 5 is the upper limit. Since we have , it means only 5 is included in the solution set. Therefore, the solution set is defined by (−4,5].
TRANSLATING MATHEMATICAL STATEMENTS INTO INEQUALITY
Translating mathematical statements into inequality can sometimes be confusing and difficult. However, these are the techniques that one must remember to avoid confusion.
- Sometimes the synonyms of greater than and less than can confuse you.
Say for example you see the statements “x is greater than 7” and “x more than 7”. While they may have the same meaning, “x is greater than 7” refers to the value of x being greater than 7. Hence, translating it to symbols will result to x > 7. However, the statement “x more than 7” refers to adding 7 to the value of x. Thus, if we translate it into algebraic expressions, this will become x + 7. - Don’t get confused with the statements “at most” and “at least”. The statement “at most” simply means the value of the variable is less than or equal to and “at least” means the value of the variable is greater than or equal to.
EXAMPLE #1
Translate 7 is greater than 5.
SOLUTION
If we translate 7 is greater than 5 into algebraic expression, it will be 7 > 5.
EXAMPLE #2
Translate the statement “the value of x is at least 10”.
SOLUTION
The key term in this statement is “at most”. “At most” when translated into algebraic terms is “less than or equal to”. Therefore, x ≤ 10.
EXAMPLE #3
James is younger than Ryan. How can you translate this statement into algebraic expression?
SOLUTION
Given that James is older than Ryan, we can say that James’ age is smaller than of Ryan’s. Thus, if we represent the age of James as x and Ryan’s age as y, we will have an inequality x < y.
EXAMPLE #4
Alyssa needs to have a minimum grade of 83 in the next quarter to pass her Math subject. How do you translate it into algebraic expression?
SOLUTION
To translate the given statement, check for the key term which is “a minimum grade of”. A minimum grade of 83 means the lowest possible grade that she should get is 83. Moreover, we must take note that the highest possible grade is 100. Therefore, translating this statement will give us the expression 83 ≤ x ≤ 100.
Recommended Worksheets
Solving Word Problems Involving Linear Equations and Linear Inequalities 7th Grade Math Worksheets
One-variable Inequalities (Time Themed) Worksheets
Understanding and Solving One-Variable Inequalities 6th Grade Math Worksheets









