Introduction
One-variable equations are fundamental to studying mathematics, as they introduce students to solving for an unknown value. This article will cover grade appropriateness, math domain, applicable Common Core Standards, definition, key concepts, examples, real-life applications, practice tests, and frequently asked questions.
Grade Appropriateness
One-variable equations are typically introduced in middle school, around 6th or 7th grade. Students continue to build upon and refine their understanding of these equations as they progress through higher-level mathematics courses.
Math Domain
Algebra is a field of mathematics dealing with symbols and the rules for manipulating them, and it is under this scope that one-variable equations are studied. Algebra is a unifying thread of almost all mathematics and includes everything from solving elementary equations to learning abstractions such as groups, rings, and fields.
Applicable Common Core Standards
One-variable equations are addressed in the following Common Core State Standards for Mathematics:
6.EE.B.5: Understand solving an equation or inequality as a process of answering a question: which values from a specified set, if any, make the equation or inequality true? Use substitution to determine whether a given number in a specified set makes an equation or inequality true.
6.EE.B.6: Use variables to represent numbers and write expressions when solving a real-world or mathematical problem; understand that a variable can represent an unknown number or, depending on the purpose at hand, any number in a specified set.
7.EE.B.4: Use variables to represent quantities in a real-world or mathematical problem and construct simple equations and inequalities to solve problems by reasoning about the quantities.
8.EE.C.7: Solve linear equations in one variable
These standards emphasize understanding, solving, and applying one-variable equations in various contexts.
Definition of the Topic
A one-variable equation is an algebraic expression that contains one unknown value, represented by a letter (usually x), and can be written in the form Ax + B = C, where A, B, and C are known numbers.
| Examples of One-Variable Equations | Non-examples of One-Variable Equations |
| 2x = 4 -m = 2 ½ r -13 = 5 5(w – 7) = 26 | 2x – 3r 11c – 5 25m – 4n + 7 100 |
Key Concepts
Coefficient: The coefficient is the numerical factor of a term with a variable.
Variable: A symbol used to represent an unknown value.
Constant: A value that does not change.
Solution: An equation’s solution is the set of variable values that makes the equation true.
Inverse operations: Operations that reverse the effects of another operation (e.g., addition and subtraction, multiplication, and division).
Solving One-Variable Equation
Take note of the following when solving the one-variable equation:
- Simplify both sides of the equation.
- Use the addition property of equality to arrange the terms that have variables on one side of the equation and constant terms on the other.
- Apply the multiplication property of the equality to set the coefficient of the variable term to 1.
- Verify your answer by substituting your solution into the original equation.
Here are the commonly used properties of equality when solving one-variable equations. If the variables a, b, and c are real numbers, then…

Discussion with Illustrative Examples
Example 1
Solve the equation x-5=8.
Solution
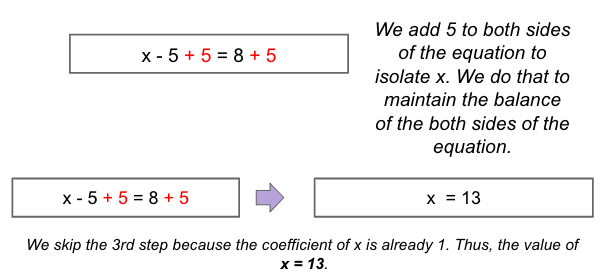

The collection of values used to replace the unknowns in an equation to make it true is known as the solution.
Example 2
Solve the equation 3x – 5 = 10.
Solution
Step 1: Add 5 to both sides of the equation.
3x – 5 + 5 = 10 + 5
Step 2: Simplify.
3x = 15
Step 3: Divide both sides by 3.
$\frac{3x}{3}$=$\frac{15}{3}$
Solution: x = 5
Example 3
The sum of two consecutive numbers is 55. Find the numbers. Use your understanding of one-variable equations to solve the problem.
Solution
Let x be a number, and x + 1 is its consecutive. Hence, the mathematical equation to show the sum is x+(x+1)=55.
Calculating the value of the numbers we have,
x+ (x+1) =55
2x+1=55
2x=55-1
2x=54
$\frac{2x}{2}$=$\frac{54}{2}$
x=27
Therefore, the two numbers are 27 and 28.
Real-life Application with Solution
Example 1
A pizza delivery service charges a flat fee of $5 per order plus $1.50 per pizza. How many pizzas must be purchased to spend $20?
Solution
Let x represent the number of pizzas ordered.
5 + 1.50x = 20
Step 1: Subtract 5 from both sides.
5 + 1.50x -5 = 20 – 5
1.50x = 15
Step 2: Divide by 1.50.
$\frac{1.50x}{1.50}$=$\frac{15}{1.50}$
Solution: 10 pizzas need to be purchased.
Example 2
Chris has x dollars. After spending $ 38 on his many school works and supplies, he will have $43 in his purse. What is the value of x?

Example 3
Clark earns $17 per day. How many days did Clark work if he received a salary of $ 204?
Solution
Let x be the number of days Clark worked. So we have,
17x=204
$\frac{17x}{17}$=$\frac{204}{17}$
x=12
Therefore, Clark worked for 12 days to earn $204.
Practice Test
A. Solve for the unknown variable. Show your complete solution.
1. 4x – 7 = 21
2. 5x + 8 = 33
3. 2m – 9 = 15
4. 7x + 5 = 40
5. 3r – 12 = 6
6. 9 – 2p = 3
7. 5x – 3 = 2x + 12
B. Answer the following questions correctly.
| 1. Is 3 a solution of 5x – 15 = 0? Prove your answer. |
| 2. Will – 4 make 2x + 13 = 5x + 20 true? Show your solution. |
| 3. Is ½ the solution of 10x – 15 = 8x + 40? |
| 4. Will x = 12 a solution to 35x – 2(x + 3) = 10x + 60? |
C. Solve the following word problems.
1. Derek works on cars. He charges $28 for each car plus $5 per hour. Write an equation representing this scenario if his customer’s car bill was $68.
2. A number is three more than twice the other number. The sum of these numbers is 30. What are the two numbers?
Frequently Asked Questions (FAQs)
What is a one-variable equation?
A one-variable equation is an algebraic expression containing one unknown value, represented by a letter, usually x.
When are one-variable equations introduced in school?
One-variable equations are typically introduced in middle school, around 6th or 7th grade.
In which branch of mathematics are one-variable equations studied?
One-variable equations are studied under the domain of algebra, which deals with symbols and the rules for manipulating these symbols.
What is the purpose of inverse operations when solving one-variable equations?
Inverse operations reverse the effects of another operation, allowing us to isolate the variable and find its value that makes the equation true.
Can one-variable equations have more than one solution?
One-variable linear equations have either one unique solution, no solution (when the equation represents parallel lines), or infinitely many solutions (when the equation represents the same line). However, other types of one-variable equations, such as quadratic equations, can have multiple distinct solutions.
Recommended Worksheets
One-Variable Equations (Employment Themed) Worksheets
One-variable Inequalities (Time Themed) Worksheets
Understanding and Solving One-Variable Equations 6th Grade Math Worksheets









