Algebraic Thinking

Definition

Algebraic thinking includes the ability to recognize patterns, represent relationships, make generalizations, and analyze how things change. Algebraic Thinking is important for developing a deep understanding of arithmetic and helps students make connections between many components of their early math studies.

Various Components of Algebraic Thinking

There are different components of algebraic thinking, some of which are – 

1. Equivalence, expressions, equations and inequalities
2. Generalizing and reasoning with arithmetic relationships
3. Functional thinking
4. Proportional Reasoning

Let us discuss about them one by one.

Equivalence, expressions, equations and inequalities

Equivalence, expressions, equations and inequalities include the development of the equal sign to express a relationship between different quantities. It also includes reasoning with expressions that are not equal and hence form an inequality.  Let us discuss these in detail.

Linear Equations

An equation in which the highest power of the variables involved is 1 is called a linear equation. In other words, a linear equation is a mathematical equation that defines a line. While each linear equation corresponds to exactly one line, each line corresponds to infinitely many equations. These equations will have a variable whose highest power is 1.

The sign of equality divides an equation into two sides, namely the left-hand side and the right-hand side, written as L.H.S and R.H.S respectively.

Linear Equations Based on the Number of Variables

We have different linear equations based on the number of variables they have. For example,

Equation with one Variable

 An equation may have only one variable such as – 

12x – 10 = 0

18x = 12

Equation with two Variables

An equation may have two variables, such as 

12x +10y – 10 = 0

12x +23y = 20

Equation with three Variables

An equation may have three variables such as

12x +10y -3z – 10 = 0

12x +23y – 12z = 20

Similarly, there can be equations that have any number of variables.  There are different methods to solve linear equations depending on the number of variables they have.

Inequalities

Inequality is a term derived from the word unequal. This means that inequality between two equations or expressions refers to the condition when they are not equal to each other. Inequality can therefore be defined as  – A statement involving variable ( s ) and the sign of inequality i.e. < , > , , or is called an inequation or an inequality. In other words, If two real numbers or algebraic expressions are related by the symbols “>”, “<”, “≥”, “≤”, then the relation is called an inequality.

An inequality may contain one or more variables. Also, it may be linear or quadratic or cubic inequation or an inequality. The less than symbol ( < ) and the greater than symbol ( > ) are the two symbols that represent strict inequality. These symbols mean that a number is strictly less than or greater than another number. Let us understand this by some examples.

We know that 2 < 5 . This means that the number 2 is strictly less than the number 5. Similarly, 9 > 3 means that the number 9 is strictly greater than the number 3.

Algebraic Expressions

An expression is a sentence with a minimum of two numbers and at least one math operation. An algebraic expression (or) a variable expression is a combination of terms by the operations such as addition, subtraction, multiplication, division, etc. an extension to the algebraic expressions are the polynomials. Also, an algebraic expression, in which variable(s) does (do) not occur in the denominator, exponents of variable(s) are whole numbers and numerical coefficients of various terms are real numbers, is called a polynomial.

Generalizing and reasoning with arithmetic relationships

Generalizing and reasoning with arithmetic relationships includes reasoning about the structure of arithmetic expressions and relationships including core properties of number and Operations.

Solving arithmetic expressions in order

In simplifying mathematical expressions consisting of the same type of operation, we perform one operation at a time generally starting from the left towards the right. If an expression has more than one fundamental operation, you cannot perform operations in the order they appear. Some operations have to be performed before than others.  This is each operation has its own precedence. Generally, the order in which we perform operations sequentially from left to right is division, multiplication, addition, subtraction. But when the expressions make use of brackets as well, we have a set of rules that defines the precedence of the operations.

Simple expressions which involve one or more than one operator can be solved using BODMAS. What is BODMAS and how it is used to solve simple expressions? Let us find out.

Order of operation can be defined as a standard procedure that guides you on which calculations to begin within an expression with several arithmetic operations. Without consistent order of operation, one can make big mistakes during computation. There are a number of rules that define the order of operations, depending upon the involvement of the operators, brackets exponents and other mathematical symbols for operations. This rule is known as BODMAS, where B stands for Brackets, O stands for Of, D stands for Division ( ÷ ), M stands for Multiplication ( x ), A stands for Addition ( + ), S stands for subtraction  ( – ).

Understanding BODAMS is integral to the understanding of the use of grouping symbols in expressions. This is because it is the BODMAS rule that defines the order in which the operations are to be performed in the case of mathematical expressions. In other words, it defines the order in which operations on numbers are to be performed when there are situations where we have two more than two operations in an expression. 

Core properties of Operations

We know that the fundamental four operations of mathematics are addition, subtraction, multiplication and division. There are some core properties that are satisfied by some of all of these four operations. These properties are – 

Closure Property – The closure property states that when an operation is performed on two numbers, the resultant would also be of the same type as the numbers on whom the operation has been performed. 

Commutative Property – Commutative Property states that when an operation is performed on two numbers, the order in which the numbers are placed does not matter. 

Associative Property – Associative Property states that when an operation is performed on more than two numbers, the order in which the numbers are placed does not matter.

Other than the above properties, there are some properties such as identity property, inverse, etc. that are defined for some of the operations only. 

Multiplicative Identity

A number is said to be an identity for multiplication, if, a number when multiplied by this identity number results in the number itself. Here, 1 is the identity element for multiplication.

Distributive Property of Multiplication over Addition / Subtraction

When two whole numbers are added or subtracted and the result is multiplied by another number, they can be multiplied separately. Therefore, for any three whole numbers, a, b and c, the distributive property of multiplication over addition states that a x ( b + c) = (a x b) + (a x c)

Functional Thinking

Functional thinking Includes representation of and reasoning with generalized relationships between co-varying quantities using verbal, symbolic, graphical, and tabular (using tables) representations.

Functions in Mathematics

The concept of function is of paramount importance in mathematics and among other disciplines as well. Functions form one of the most important building blocks of Mathematics. The word function has been derived from the Latin word meaning operation and the words mapping and map are synonymous with it. Functions play an important role in differential and integral calculus.

Let A and B be two non-empty sets. A relation f from A to B, i.e. a subset of A x B is called a function or a mapping or a map from A to B is,

1. For each a ∈ A there exists b B such that ( a, b ) ∈ f
2. ( a, b ) ∈ f and ( a, c ) ∈ f ⇒ b = c

Thus a non-void set f of A x B is a function from A to B if each element of A appears in some ordered pair in f and no two ordered pairs in f have the same first element.

If ( a, b ) ∈ f, then b is called the image of a under f.

Real Functions

Some functions have domain and co-domain both as subsets of the set R of all real numbers. Such functions are called real functions or real valued functions of the real variable. In other words, a function f : A → B is called a real valued function, if B is a subset of R, where R is the set of all real numbers.

Graphical representation of Operations on Functions

Let us discuss the graphical representation of two operations on functions, namely addition and subtraction.

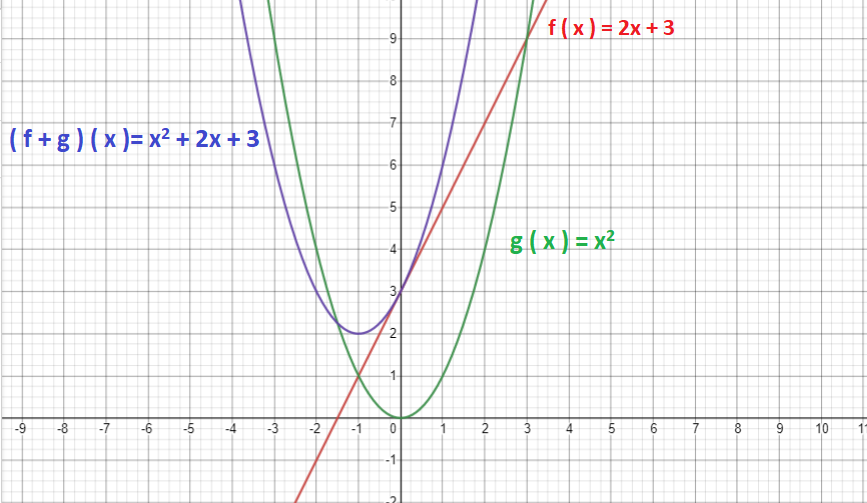
Graphical Representation of Addition of Functions 

Let f ( x ) = 2x + 3 and g ( x ) = x²

f ( x ) + g ( x ) = 2x + 3 + x²

( f + g ) ( x )= x² + 2x + 3

The graphs of these two functions and their addition will be represented as 

Graphical Representation of Subtraction of Functions 

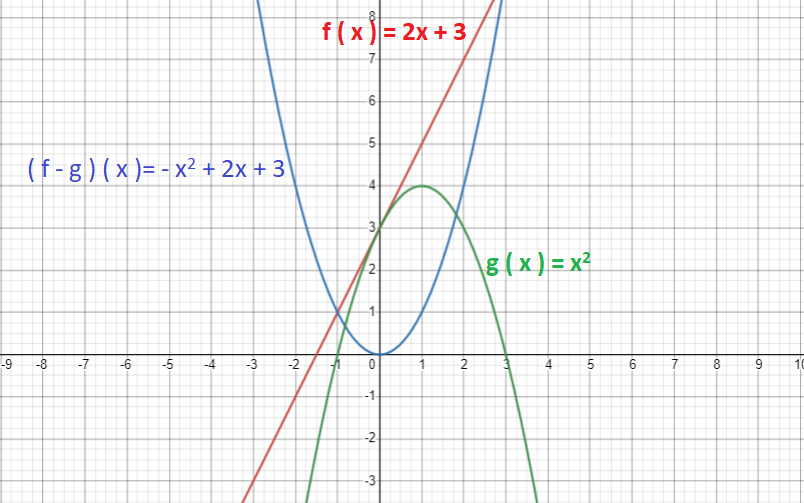
Let f ( x ) = 2x + 3 and g ( x ) = x²

f ( x ) – g ( x ) = 2x + 3 – x²

( f – g ) ( x )= – x² + 2x + 3

The graphs of these two functions and their subtraction will be represented as 

Proportional Reasoning

Proportional reasoning includes reasoning abstractly about the relationship between two generalized quantities. This introduces us to the concept of ratio and proportion.

Ratio

The ratio of two quantities of the same kind and in the same units is a fraction that shows how many times a quantity is of another quantity of the same kind. The ratio of two numbers “ a “ and “ b “ where b ≠ 0, is a ÷ b or $\frac{a}{b}$ and is denoted by a : b

In the ratio, a : b, the quantities or numbers a and b are called the terms of the ratio. The former “ a” is called the first term or antecedent and the latter term “ b” is called the second term or consequent.

Let us understand the ratio with the help of an example.

Suppose we have two brothers, Sam and Peter having their weights as 50 kg and d40 kg respectively. Now, if we compare the weight of Sam with the weight of Peter, we will get

$\frac{Weight\: of\: Sam}{Weight\: of\: Peter} = \frac{50}{40} = \frac{5}{4}$ = 5 : 4 

Hence, we can say that the ratio of the weight of Sam to the weight of Peter is 5 : 4.

Proportion

Proportion is an equality of two ratios. For example, consider two ratios, 6 : 18 and 8 : 24. We can see that

6 : 18 = 1 : 3 and 8 : 24 = 1 : 3

Therefore, 6 : 18 = 8 : 24

Thus the ratios 6 : 18 and 8 : 24 are in proportion.

Therefore, we can say that four numbers a, b, c and d are said to be in proportion if the ratio of the first two is equal to the ratio of the last two. This means, four numbers a, b, c and d are said to be in proportion, if a : b =  c : d

If four numbers a, b, c and d are said to be in proportion, then we write

a : b : : c : d

which is read as “ a is to b as c is to d” or “ a to b as c to d”. Here a, b, c and are the first second, third and fourth terms of the proportion. The first and the fourth terms of the proportion are called extreme terms or extremes. The second and the third terms are called the middle terms or means.

Let us understand this by an example.

Consider four terms 40, 70, 200 and 350. We find that 40 : 70 = 200 : 350. So, the given numbers are in proportion. Clearly, 40 and 350 are extreme terms and 70 and 200 are middle terms. We find that,

Product of extreme terms  = 40 x 350 = 14000

Similarly, product of middle terms = 70 x 20 = 14000

Therefore,

Product of extreme terms = Product of middle terms

Thus, we can say that if four numbers are in proportion then the product of the extreme terms is equal to the product of the middle terms.

Continued Proportion 

Three numbers a b c are said to be in continued proportion if a, b, b, c are in proportion.

Thus, if a, b and c are in proportion, then we have a : b : : b : c

Product of extreme terms = Product of middle terms

⇒ a x c = b  x b

⇒ a c  = b ²

⇒ b ² = a c

Mean Proportion

If a, b and c are in continued proportion then b is called the mean proportional between a and c. This means that if b is the mean proportional between a and c then b ² is equal to  a c.

Key Facts and Summary

1. Algebraic thinking includes the ability to recognize patterns, represent relationships, make generalizations, and analyze how things change. 
2. Equivalence, expressions, equations and inequalities includes the development of the equal sign to express a relationship between different quantities. It also includes reasoning with expressions that are not equal and hence form an inequality.  
3. An equation in which the highest power of the variables involved is 1 is called a linear equation.
4. Inequality is a term derived from the word unequal. This means that inequality between two equations or expressions refers to the condition when they are not equal to each other.
5. Generalizing and reasoning with arithmetic relationships includes reasoning about the structure of arithmetic expressions and relationships including core properties of number and Operations.
6. In simplifying mathematical expressions consisting of the same type of operation, we perform one operation at a time generally starring from the left towards the right.
7. The closure property states that when an operation is performed on two numbers, the resultant would also be of the same type as the numbers on whom the operation has been performed. 
8. Commutative Property states that when an operation is performed on two numbers, the order in which the numbers are placed does not matter. 
9. Associative Property states that when an operation is performed on more than two numbers, the order in which the numbers are placed does not matter.
10. Functional thinking Includes representation of and reasoning with generalized relationships between co-varying quantities using verbal, symbolic, graphical, and tabular (using tables) representations.
11. The ratio of two quantities of the same kind and in the same units is a fraction that shows how many times a quantity is of another quantity of the same kind. The ratio of two numbers “ a “ and “ b “ where b ≠ 0, is a ÷ b or $\frac{a}{b}$ and is denoted by a : b
12. Four numbers a, b, c and d are said to be in proportion if the ratio of the first two is equal to the ratio of the last two. This means, four numbers a, b, c and d are said to be in proportion, if a : b =  c : d

Recommended Worksheets

Algebraic Expressions (International Yoga Day Themed) Worksheets
Addition of Rational Algebraic Expressions with Same Denominators (School Themed) Worksheets
Division of Rational Algebraic Expressions with Same Denominators (Festa Junina Themed) Worksheets