Equation

DEFINITION OF EQUATION

A mathematical equation is a statement of equality between two mathematical expressions which is connected by an equal sign. The two mathematical expressions are connected by an equal sign to assert that they have the same value.

PARTS OF AN EQUATION

The mathematical expressions on the two sides of the equal sign are called “left-hand side” and “right-hand side” of the equation, respectively.

Let’s say we have 7x+5 on the left-hand side and19 on the right-hand side, we can name its parts as:

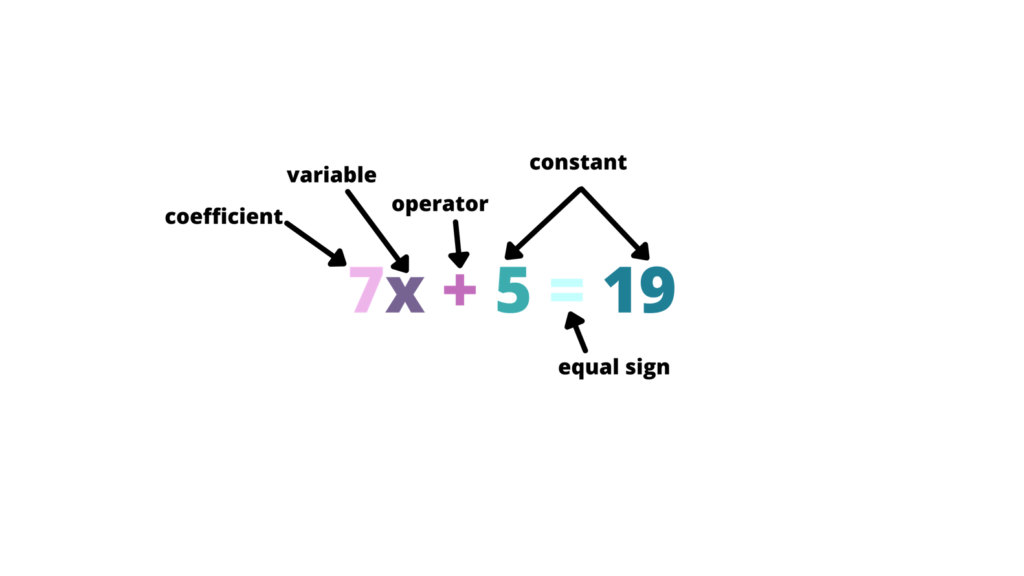
• A coefficient refers to a number that is being multiplied by the variable.
• A variable is a symbol or any letter that works as a placeholder for a quantity that may assume any given value.
• An operator is a symbol that indicates an operation to be performed, such as addition, subtraction, multiplication, etc.
• A constant term is a value or quantity that does not change. It is the fixed value in a mathematical statement.
• An equal sign is a mathematical symbol that indicates the equality of two values.

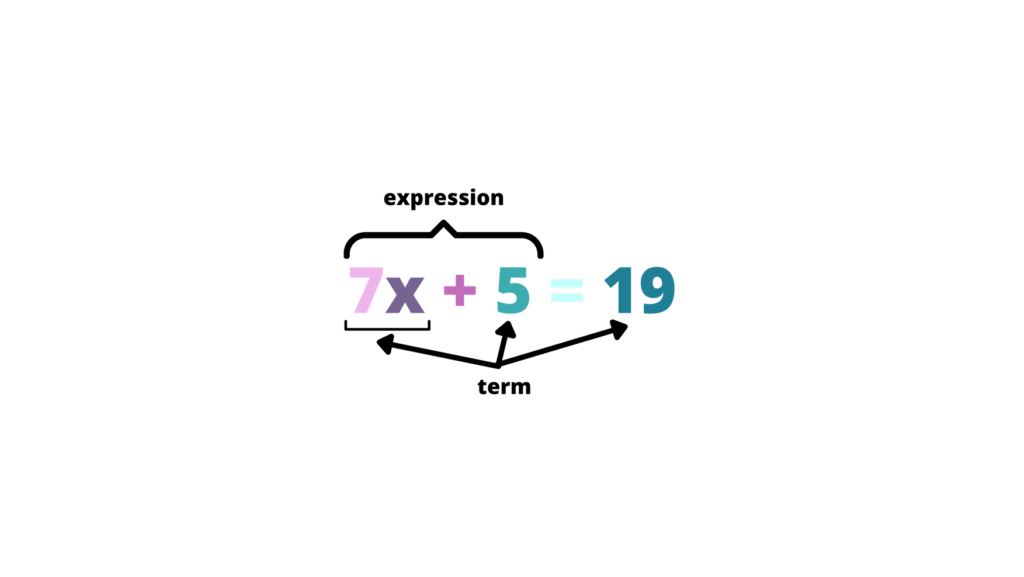
• A term can be a constant number, a variable, or a combination of constant and variable/s.
• An expression is made up of terms and at least one operator.

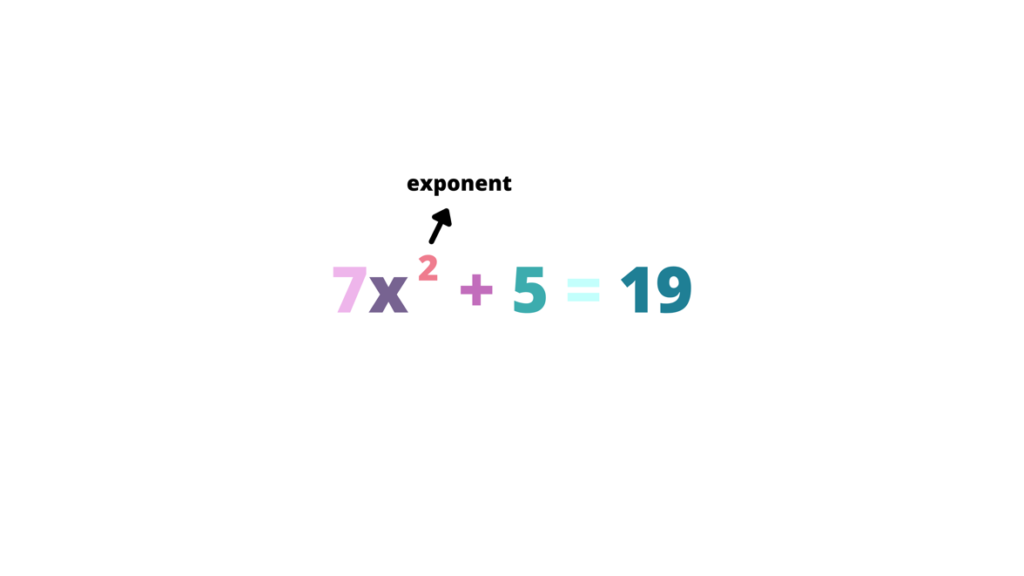
• An exponent indicates the number of a times a number is multiplied by itself.

PROPERTIES OF EQUALITY

The list below shows the properties of equality for all real numbers. These properties will help you solve equations.

REFLEXIVE PROPERTY

Reflexive property states that a number is equal to itself. Hence, for all real numbers x,

x=x

SYMMETRIC PROPERTY

In symmetric property, the order of equality does not matter. Thus, for all real numbers x and y,

if x=y, then y=x

TRANSITIVE PROPERTY

Transitive property states that if two numbers are equal to the same number, then they are also equal. Thus, for all real numbers x, y, and z,

if x=y and y=z, then x=z

ADDITION PROPERTY

For all real numbers x, y, and z,

if x=y, then x+z=y+z

SUBTRACTION PROPERTY

For all real numbers x, y, and z,

if x=y, then x-z=x-z

MULTIPLICATION PROPERTY

For all real numbers x, y, and z,

if x=y, then xz=yz

DIVISION PROPERTY

For all real numbers x, y, and z,

if x=y and $z\neq 0$, then $\frac{x}{z}=\frac{y}{z}$.

DISTRIBUTIVE PROPERTY

For all real numbers x, y, and z,

x(y+z)=xy+yz

LINEAR EQUATION

DEFINITION OF LINEAR EQUATION

Linear equations are equations of degree one. It is an equation used to define the lines in a coordinate system.

LINEAR EQUATION	NON-LINEAR EQUATION
3x – 7 = 20	6xy=24
5y = 4x + 15	$y^{2}+7y=8$
7x +2y + z = 14	$3x+xy+y^{2}=21$

FORMS OF LINEAR EQUATION

Linear equations can be written in various ways.

STANDARD FORM

The standard form of linear equation is

ax+by+c=0

where a, b and c are real numbers and x and y are variables.

SLOPE-INTERCEPT FORM

The slope-intercept form is the most common form of linear equation. It is represented as:

y=mx+b

where,

m is the slope of the line

b is the y-intercept

For example, y=2x+6. We can easily define the slope of the line and the y-intercept.

Hence, m=2 and b=7.

POINT-SLOPE FORM

The form point-slope for linear equations emphasizes the slope of the line and a point on the line (that is not the y-intercept). It is represented as:

$y-y_{1}=m(x-x_{1})$

where,

 $(x_{1},y_{1})$ are the coordinates of the point

 m is the slope of the line

For example, y-10=3(x-8). The coordinates of the point is (8,10) and the slope of the line is 3.

INTERCEPT FORM

Intercept form emphasizes the x and y intercept of the line. The x-intercept is the shortest distance of the point on the x-axis from the origin, wherein the y-intercept is the shortest distance of the point on the y-axis from the origin. It is represented as:

$\frac{x}{a}+\frac{y}{b}=1$

where,

a is the x-intercept

b is the y-intercept

For example, $\frac{x}{9}-\frac{y}{11}=1$. The x -intercept in the given equation is 9 and y -intercept is 11.

TWO-POINT FORM
A two-point form is used for finding the equation of a line if two points are given.

$y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$

where,

$(x_{1},y_{1})$ are the coordinates of the first point

$(x_{2},y_{2})$ are the coordinates of the second point

Example: Find the equation of a line passing through points A(6,2) and B(-3,5).

Solution:

$y-2=\frac{5-2}{-3-6}(x-6)$

$y-2=\frac{3}{-9}(x-6)$

$y-2=-\frac{1}{3}(x-6)$

$y-2=-\frac{1}{3}x+\frac{6}{3}$

$y-2=-\frac{1}{3}x+2$

$y=-\frac{1}{3}x+4$

Therefore, the equation of the lines given is  where  and b=4.

LINEAR EQUATION IN ONE VARIABLE

A linear equation in one variable is an equation with a standard form of

ax+b=0,

where a and b are real numbers and x is a variable.

In the general case where $a\neq 0$, linear equation in one variable has one unique solution of  $x=-\frac{b}{a}$.

TYPES OF LINEAR EQUATION IN ONE VARIABLE

Linear equation in one variable can be classified as identity, conditional, or inconsistent.

IDENTITY EQUATION

An identity equation is true for all the values of the variable. Hence, the solution set of an identity equation is the set of all real numbers. For example,

8x=11-3x

Substituting any real number to the value to x will make the equation true. We can denote the solution set of an identity equation as {$x\mid x \epsilon \mathbb{R}$}.

CONDITIONAL EQUATION

A conditional equation is only true for some values of the variable. Thus, the solution set of a conditional equation consists of one number. For example, solving for the equation 7x – 9 = 3x + 27 will result in:

7x – 9 = 3x + 27

7x – 3x = 27 + 9

4x = 36

$\frac{4x}{4}=\frac{36}{4}$

x = 9

Therefore, the solution set of 7x – 9 = 3x + 27 is {9}. Conditional equation has only one solution that will make the equation true.

INCONSISTENT EQUATION

An inconsistent equation results in a false statement. Thus, there is no solution for any inconsistent equation. For example, solving for the equation 6x – 9 = 6x – 18 will result in:

6x – 9 = 6x – 18

6x – 9 – 6x = 6x – 18 – 6x

$-9\neq -18$

Since -9 is not equal -18, we can conclude that this equation has no solution.

SOLVING LINEAR EQUATION IN ONE VARIABLE

There is no step-by-step order in solving linear equation in one variable as the steps depends on the given equation. However, there are strategies that will help you easily solve it.

1. Clear any fractions. If an equation contains any fractions, find the least common denominator then multiply it to both sides of the equation.
2. Always remember that whatever operation or process you do on the left-hand side, you also need do it on the right-hand side.
3. Keep in mind all the properties of equality.
4. Always isolate the variable on one side of the equation.
5. Don’t forget to simplify your answer in its lowest form.
   

EXAMPLE #1

Solve for the value of x in the equation 2x – 4 = 18.

SOLUTION

To solve for the value of x,

2x – 4 = 18

2x – 4 + 4 = 18 + 4 Add 4 on both sides

2x = 22

$\frac{2x}{2}=\frac{22}{2}$ Divide both sides by the coefficient of x

x = 11

Therefore, the value of x is 11.

EXAMPLE #2

Find the solution of 8(x+2) + 1= 19 – 9(5-x).

SOLUTION

To find the solution for the given linear equation,

8(x+2) + 1 = 19 – 9(5 – x) Use distributive property of equality

8x + 16 + 1 = 19 – 45 + 9x

8x + 17 = -26 + 9x Combine like terms

8x + 17 – 8x = -26 + 9x – 8x Subtract 8x on both sides

8x – 8x + 17 = -26 + 9x – 8x Combine like terms

17 = -26 + x

17 + 26 = -26 + x + 26 Add 26 on both sides.

17 + 26 = -26 + 26 + x Combine like terms

43 = x

Thus, the solution of the equation is 43.

LINEAR EQUATION IN TWO VARIABLES

An equation is said to be a linear equation in two variables if it is in the form:

ax + by + c = 0

where a,b and c are real numbers and  and  are variables.

LINEAR EQUATION IN TWO VARIABLES	NOT
2x-7y=6	2xy=6
-5x-3y=15	$-5x^{2}-3y=15$

LINEAR EQUATION IN THREE VARIABLES

A linear equation in three variables is represented in the form of

ax + by + cz + d = 0

where a, b, c, and d are real numbers and x, y, and z are variables.

LINEAR EQUATION IN TWO VARIABLES	NOT
x+9y+9z-5=0	xy+9x+8yz-5=0
-8x+2y+z=26	$8x+2x^{2}+z^{3}=26$

SYSTEMS OF LINEAR EQUATION

DEFINITION OF LINEAR SYSTEM

A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are simultaneously work together.

TYPES OF LINEAR SYSTEM

There are only three types of systems of linear equations in two variables.

1. Independent System

It is a system of linear equation with exactly one solution pair. The intersection of two lines is the only solution of this linear system.

Types of Solutions and their Graphs, digital photograph, Cuemath, www.cuemath.com/algebra/linear-equations-in-two-variables/. Accessed 18 Sept. 2021.

2. Inconsistent System

An inconsistent system has no solution. The graph of an inconsistent system is a parallel line.

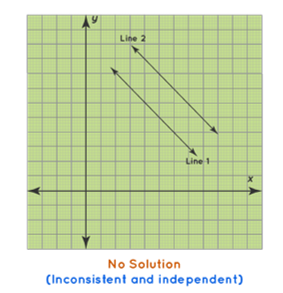
Types of Solutions and their Graphs, digital photograph, Cuemath, www.cuemath.com/algebra/linear-equations-in-two-variables/. Accessed 18 Sept. 2021.

3. Dependent System

A dependent system has infinitely many solutions wherein the lines coincides with each other.

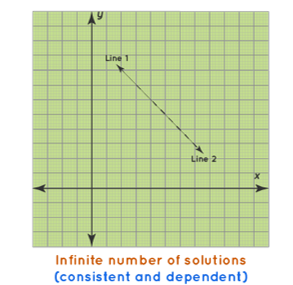
Types of Solutions and their Graphs, digital photograph, Cuemath, www.cuemath.com/algebra/linear-equations-in-two-variables/. Accessed 18 Sept. 2021.

SOLVING SYSTEMS OF LINEAR EQUATION

There are various methods in finding the solution set of linear system with two variables.

1. Substitution Method

Substitution method is one of the simplest way to solve systems of linear equations. This method works by simply finding the value of x-variable in terms of y-variable, then replacing the value of x-variable in the second equation. In order to use the substitution method, we follow the steps below:

Step 1: Use one of the equations to find x  in terms of y or y in terms of x.

Step 2: Substitute this in the other equation to get an equation in terms of the single variable.

Step 3: Solve for the value of the variable.

Step 4: Substitute to value of the variable to any of the equations to get the value of another variable.

EXAMPLE

Find the coordinates of the point where y=4x-9 and y=x-3 will intersect using substitution method.

 SOLUTION

y = 4x -9 (1)
y = x-3 (2) Substitute the equation 1 to the y-variable of equation 2

4x – 9 = x – 3
4x – x = -3 + 9 Addition Property of Equality
3x = 6
$\frac{3x}{3}=\frac{6}{3}$ Multiplication Property of Equality
x = 2

y = 4x – 9
y = 4(2) – 9 Substitute x=2 to equation 1
y = 8 – 9
y = -1

2. Elimination Method

The process of eliminating one of the variables in the system of linear equations using either addition or subtraction in conjunction with multiplication or division of coefficients of the variables is called elimination method. To solve a system of linear equation in two variables using elimination method, use the steps given below:

Step 1: Arrange the equations in form, ax+by=c.

Step 2: Check if adding or subtracting the equations will result in the cancellation of a certain variable.

Step 3: If step 2 does not work, multiply one or both equations by the coefficient of either x or y.

Step 4: Solve for the value of the variable.

Step 5: Substitute the value of the variable to any of the equations to get the value of another variable.

EXAMPLE

Using the elimination method, find the solution of the equations 2x+4y=-10 and 7x+8y=-23.

SOLUTION

2x + 4y = -10 (1)
7x + 8y = -23 (2)

-2(2x + 4y) = (-10 )-2 Multiply -2 to equation 1 since we need to eliminate 8y
-4x – 8y = 20

-4x – 8y = 20
7x + 8y = -23 Add the two equations
3x = -3
$\frac{3x}{3}=\frac{-3}{3}$ Multiplication Property of Equality
x = -1

2x + 4y = -10
2(-1) + 4y = -10 Substitute x=-1 to equation 1
-2 + 4y = -10
4y = -10 + 2 Addition Property of Equality
4y = -8
$\frac{4y}{4}=\frac{-8}{4}$ Multiplication Property of Equality
y = -2

3. Graphical Method

To steps below shows how to solve a system of linear equations graphically,

Step 1: Convert the equations in a slope-intercept form, y=mx+b

Step 2: Make a table of values by assuming the any values for x

Step 3: The point of intersection of the two lines is the solution of equation.

EXAMPLE

By graphing, what is the solution of the lines x-y=3 and 7x-y=-3?

x – y = 3
-y = 3 – x
$\frac{-y}{-1}=\frac{3-x}{-1}$
y = -3 + x
y = x – 3

7x – y = -3
-y = -3 – 7x
$\frac{-y}{-1}=\frac{3-7x}{-1}$
y = 3 + 7x
y = 7x + 3

SOLUTION

Convert the equation in a slope intercept form:

Make a table of values:

x	-2	-1	0	1	2
y	-5	-4	-3	-2	-1

x	-2	-1	0	1	2
y	-11	-4	3	10	17

Graph the two lines in one coordinate system.

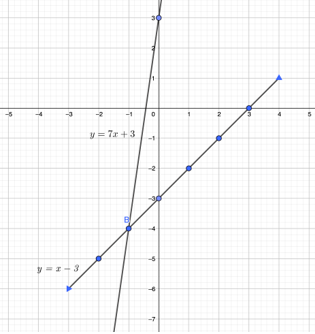
Therefore, the solution of the equation is at point (-1,-4).

QUADRATIC EQUATION

DEFINITION OF QUADRATIC EQUATION

Quadratic equations are equations of degree two with a general form of

$ax^{2}+bx+c=0$

 where x is a variable and a, b, c is a constant term such that .

SOLVING QUADRATIC EQUATIONS

In solving quadratic equations, one must take note quadratic equations have 2 solutions. There are many ways to solve quadratic equations, some of them is listed below:

1. Solving by Factoring

Factoring is the process of finding the common factors between two algebraic expressions. Solving by factoring doesn’t always work especially but it is the simplest way to solve for the solutions of quadratic equations. To use this method, we can follow the steps below:

Step 1: Make sure that the equation is in the form, $ax^{2}+bx+c=0$ .

Step 2: Find the factors of the constant term such that the sum of the factors is equal to the middle term of the equation.

Step 3: Solve for the solutions of the quadratic equation by equating the two factors to zero.

EXAMPLE #1

Find the solution of the quadratic equation $x^{2}+x=12$ by factoring.

SOLUTION

Convert to standard form.

$x^{2}+x=12$

$x^{2}+x-12=0$

Check the possible factors of  that if you add the factors, it will result to 1.

$x^{2}+x-12=0$

$(x+4)(x-3)=0$

Equate the two factors two zero.

$(x+4)=0$

$x+4=0$

$x=-4$

$(x-3)=0$

$x-3=0$

$x=3$

Therefore, the solutions of the equation is x=-4 and x=3. We can also denote it as x = {-4, 3}.

EXAMPLE #2

By factoring, determine the solution of $8x^{2}=21x$.

SOLUTION

Convert to standard form.

$8x^{2}=21x$

$8x^{2}-21x=0$

Since there is no constant term, we can easily factor out the GCF between the two algebraic terms.

$8x^{2}-21x=0$

$x(8x-21)=0$

Equate the two factors two zero.

$x=0$

$8x-21=0$

$x=\frac{21}{8}$

Hence, the solutions of the equation is x=0 and $x=\frac{21}{8}$ or we can write it as x={0, $\frac{21}{8}$ }.

EXAMPLE #3

Find the solution of $4x^{2}-1=0$.

SOLUTION

Notice the first term and the constant term. This example is a special case since both of them are squares of a number, which we call difference of two squares. Factoring the difference of two squares will give us the form

$a^{2}-b^{2}=(a+b)(a-b)$

Therefore,

Get the square root of $4x^{2}$ and 1.

$4x^{2}-1=0$

$(2x-1)(2x+1)=0$

Equate the two factors two zero.

$2x-1=0$

$2x=1$

$\frac{2x}{2}=\frac{1}{2}$

$x=\frac{1}{2}$

$2x+1=0$

$2x=-1$

$\frac{2x}{2}=\frac{-1}{2}$

$x=-\frac{1}{2}$

Therefore, the solution is x = {$\frac{-1}{2}, \frac{1}{2}$}.

2. Completing the Square

This method is often used in any computation involving quadratic polynomials. The steps on how to complete the square is listed below:

Step 1: Convert the equation in the form $ax^{2}+bx=c$.

Step 2: Divide all terms by the leading coefficient, which will make the form

$x^{2}+\frac{b}{a}x=\frac{c}{a}$

Step 3: Add a value on the left-hand side that will make it a perfect square.

Step 4: Add the same value on the right-hand side.

Step 5: Get the square root of both sides of the equation.

Step 6: Solve for the value of x.

EXAMPLE

Solve for the value of x given the equation $x^{2}-6x+1=0$.

SOLUTION

Convert the equation in the form $ax^{2}+bx=c$.

$x^{2}-6x+1=0$

$x^{2}-6x=-1$

To make the left-hand side a perfect square, divide the numerical coefficient of x by 2, then square it to get the constant term needed for the left hand side.

$x^{2}-6x=-1$

$x^{2}-6x+9=-1+9$

$(x-3)^{2}=8$

Get the square root of the two sides of the equation.

$(x-3)^{2}=8$

$\sqrt{(x-3)^{2}}=\sqrt{8}$

$x-3=\pm 2\sqrt{2}$

Solve for the values of x.

$x-3=\pm 2\sqrt{2}$

$x=\pm 2\sqrt{2}+3$

$x=3\pm 2\sqrt{2}$

Therefore, the values of x is $ 3\pm 2\sqrt{2} $.

3. Quadratic Formula

This method will always work in solving quadratic equations. The quadratic formula is shown below:

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

where,

a is the numerical coefficient of the leading coefficient

b is the numerical coefficient of the middle term

c is the constant term

Using this method, you will simply substitute all the numerical coefficients and constant term in the given formula. Take note to always convert the equation to standard form before using this formula to avoid confusion.

EXAMPLE

Find the roots of the quadratic equation $x^{2}+2x=7$.

SOLUTION

Convert the equation in standard form

$x^{2}+2x=7$

$x^{2}+2x-7=0$

Define the values of  a, b, c.

$a=1,b=2,c=-7$

Use the quadratic formula and substitute the values of

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

$x=\frac{-2\pm \sqrt{2^{2}-4(1)(-7)}}{2(1)}$

$x=\frac{-2\pm \sqrt{4+28}}{2}$

$x=\frac{-2\pm \sqrt{32}}{2}$

$x=\frac{-2\pm 4\sqrt{2}}{2}$

$x=-1\pm 2\sqrt{2}$

Therefore, the roots of the equation is $x=-1\pm 2\sqrt{2}$.

RATIONAL EQUATION

DEFINITION OF RATIONAL EQUATION

If an equation contains at least one rational expression, it is called a rational equation. Take note that a rational expression is the ratio of two polynomials.

RATIONAL EQUATION	NOT A RATIONAL EQUATION
$\frac{2}{x}+3=4x$	$\frac{4x}{3}+7=1$
$\frac{3}{4+x}$	$\frac{3x-4}{5}=\frac{7}{6}$
$\frac{x+1}{x+3}+\frac{x}{x-3}=6$	$\frac{(x+3)(x-3)}{2}=\frac{x+7}{4}$

SOLVING RATIONAL EQUATION

The steps to solve a rational equation are:

Step 1: Find the least common denominator (LCD) of the algebraic terms.

Step 2: Multiply the LCD to the both sides of the equation.

Step 3: Simplify, if necessary.

Step 4: Solve for the value of the unknown.

Step 5: Double check your answer to avoid extraneous values.

EXAMPLE #1
Find the value of x in $\frac{6}{x}-\frac{1}{3}=\frac{3}{x}$.

SOLUTION

$\frac{6}{x}-\frac{1}{3}=\frac{3}{x}$ LCD is 2x

$(2x)(\frac{6}{x}-\frac{1}{3})=(\frac{3}{x})(2x)$ Multiply the LCD to both sides of the equation

$12-x=6$

$-x=6-12$

$-x=-6$ Addition Property of Equality

$\frac{-x}{-1}=\frac{-6}{-1}$ Multiplication Property of Equality

$x=6$

Therefore, the value of x that will make the statement true is 6.

EXAMPLE #2
Solve for the value of x given $5-\frac{1}{x^{2}+x}=\frac{7}{x+1}$.

SOLUTION

$5-\frac{1}{x^{2}+x}=\frac{7}{x+1}$

$(x^{2}+x)(5-\frac{1}{x^{2}+x})=(\frac{7}{x+1})(x^{2}+x)$

$5(x^{2}+x)-1=7x$

$5x^{2}+5x-1=7x$

$5x^{2}+5x-7x-1=0$

$5x^{2}-2x-1=0$

Use quadratic equation formula to solve for the value of x.

$x=\frac{-(-2)\pm \sqrt{(-2)^{2}-4(5)(-1)}}{2(5)}$

$x=\frac{2\pm \sqrt{4+20}}{10}$

$x=\frac{2\pm \sqrt{24}}{10}$

$x=\frac{2\pm 2\sqrt{6}}{10}$

$x=\frac{1\pm \sqrt{6}}{5}$

Therefore, the values of x are $x=\frac{1\pm \sqrt{6}}{5}$.

RADICAL EQUATION

DEFINITION OF RADICAL EQUATION

An equation is said to be a radical equation if the algebraic expression is inside a radical symbol or if a variable has a rational exponent.

RADICAL EQUATION	NOT A RADICAL EQUATION
$\sqrt{x+3}=4$	$x+\sqrt{4}=5$
$x^{\frac{1}{2}}+49=0$	$3x+81^{\frac{1}{3}}=0$

SOLVING RADICAL EQUATION

The key steps in solving radical equations are:

Step 1: Isolate the radical symbol on one side of the equation.

Step 2: Square both sides of the equation.

Step 3: Solve for the value of x.

Step 4: Double check your answer to avoid extraneous values.

EXAMPLE #1

Solve for the possible value of x in $\sqrt{x+4}=7$.

SOLUTION

$\sqrt{x+4}=7$

$(\sqrt{x+4})^{2}=7^{2}$

$x+4=49$

$x=49-4$

$x=45$

Therefore, the value of x is 45.

EXAMPLE #2

Solve for the possible value of x in $\sqrt{5+2x}=x+3$.

SOLUTION

$\sqrt{5+2x}=x+3$

$(\sqrt{5+2x})^{2}=(x+3)^{2}$

$5+2x=x^{2}+6x+9$

$x^{2}+6x-2x+9-5=0$

$x^{2}+4x+4=0$

Solve for the value of x by factorization.

$x^{2}+4x+4=0$

$(x+2)(x+2)=0$

Equate the factors to zero.

$x+2=0$

$x=-2$

Therefore, the value of x is -2.

EXPONENTIAL EQUATION

DEFINITION OF EXPONENTIAL EQUATION

Exponential equations are equations with exponents where the exponent has a variable.

EXPONENTIAL EQUATION	NOT AN EXPONENTIAL EQUATION
$4^{x+1}=16$	$3^{7}=x$
$3^{x}+7^{x+1}=49$	$x^{3}+7x^{2}=49$

TYPES OF EXPONENTIAL EQUATION

There are three types of exponential equations, namely:

1. Exponential equations with the same bases
2. Exponential equations with different bases that can be worked out to be the same
3. Exponential equation with different bases that cannot be the same.

SOLVING EXPONENTIAL EQUATION WITH SAME BASE

In solving exponential equation with the same base, take note of the fact that if:

$b^{x}=b^{y}$, then $x=y$

where,

b is the base number
x,y is the exponent

EXAMPLE
Determine the value of x given $4^{2x+3}=4^{7}$.

SOLUTION

$4^{2x+3}=4^{7}$

$2x+3=7$, $b^{x}=b^{y}$, then $x=y$

$2x=7-3$ Addition Property of Equality

$2x=4$

$\frac{2x}{2}=\frac{4}{2}$ Multiplication Property of Equality

$x=2$

Therefore, the value of x is 2.

SOLVING EXPONENTIAL EQUATION WITH DIFFERENT BASE

There are two methods in which we can solve an exponential equation with different bases these are:

1. If possible, work out the bases if it can be the same
2. Converting the exponential equation into a logarithmic form, $b^{x}=a\Leftrightarrow \log _{b}a=x$.
3. Applying the property of logarithm, $\log a^{m}=m\log a$.

EXAMPLE #1

Find the value of x given the equation $3^{x}=27^{x+5}$.

SOLUTION
Work out the bases to make it the same. Since $27=3^{3}$, we can substitute it so that:

$3^{x}=27^{x+5}$

$3^{x}=3^{3(x+5)}$

Since, $b^{x}=b^{y}$, then $x=y$.

$x=3(x+5)$

$x=3x+15$

$x-3x=15$

$-2x=15$

$\frac{-2x}{-2}=\frac{15}{-2}$

$x=-\frac{15}{2}$

Thus, $ x=-\frac{15}{2} $.

EXAMPLE #2

Find the value of x given the equation $9^{x}=4^{2}$.

SOLUTION

Apply the rule, $b^{x}=a\Leftrightarrow \log _{b}a=x$.

$9^{x}=4^{2}$

$x\log 9=2\log 4$

$\frac{x\log 9}{\log 9}=2(\frac{\log 4}{\log 9})$

$x=2(0.63)$

$x=1.26$

Therefore, the value of x is approximately 1.26.

Recommended Worksheets

One-Variable Equations (Employment Themed) Worksheets
Graphing and Solving Systems of Linear Equations in Two Variables 8th Grade Math Worksheets
Applying the Properties of Equalities Involving Linear Equations 7th Grade Math Worksheets