Definition
The topic of number changing is covered here. Number change is the knowledge that we either add to or subtract from one number to make another number, together with the understanding of how much to add or subtract.
Let us change the number 358 as an example, and let us see what happens if we change the number from 3 to 2 in the hundreds place. The number will be 158 since we took away 1 hundred.
Let us first review the idea of place value and how it affects the change that occurs to a number before we continue our discussion of number change and look at further instances.
Place Value and Place Value Chart
In mathematics, each digit in a number has a place value. The value a digit in a number represents based on where it is in the number is known as place value.
The placement of each digit represents value. These positions begin at the unit place, often known as the ones position. Ones/unit, tens, hundreds, thousands, ten thousands, one hundred thousands, and so on are the place values of a number’s digits from right to left.
An illustration that enables us to locate and contrast the place values of the digits in numbers up to millions is known as a place value chart. As we move from left to right on the place value chart, a digit’s place value goes up by ten times and down by ten times.

Let us say, for example, in the number 654, 321
6 is in the hundred thousands place with a place value of 600,000.
5 is in the ten thousands place with a place value of 50,000.
4 is in the thousands place with a place value of 4,000.
3 is in the hundreds place with a place value of 300.
2 is in the tens place with a place value of 20.
1 is in the ones place with a place value of 1.
By multiplying the face value with the actual value of the number, one can get a number’s place value. A one-digit number has a place value equal to its face value. For instance, 1, 2, 3, 4, 5, 6, 7, 8, and 9 have the same place value and face value as 1, 2, 3, 4, 5, 6, 7, 8, and 9, respectively. Any number’s place value for zero is always zero. Zero may appear anywhere in a number, but it will always have zero value.
Examples
Example 1
In the number 594, write down the place value of the digits.
Answer:
The value of the digit 4, which is in the ones, is 4 x 1 = 4
The value of the digit 9, which is in the tens place, is 9 x 10 = 90
The value of the digit 5, which is in the hundreds place, is 5 x 100 = 500
Example 2
For the number 456 897, write down the place value of each digit.
Answer:
The value of the digit 7, which is in the ones place, is 7 x 1 = 7.
The value of the digit 9, which is in the tens place, is 9 x 10 = 90.
The value of the digit 8, which is in the hundreds place, is 8 x 100 = 800.
The value of the digit 6, which is in the thousands place, is 6 x 1000 = 6000.
The value of the digit 5, which is in the ten thousands place, is 5 x 10000 = 50000.
The value of the digit 4, which is in the hundred thousands place, is 4 x 100000 = 400000.
Example 3
For the number 90 165 478, write down the place value of each digit.
Answer:
The value of digit 8, which is in the ones place, 8 x 1 = 8.
The value of digit 7, which is in the tens place, 7 x 10 = 70.
The value of digit 4, which is in the hundreds place, 4 x 100 = 400.
The value of digit 5, which is in the thousands place, 5 x 1000 = 5000.
The value of digit 6, which is in the ten thousands place, is 6 x 10000 = 60000.
The value of digit 1, which is in the hundred thousands place, is 1 x 100000 = 100000.
The value of digit 0, which is in the millions place, is 0 x 1000000 = 0.
The value of digit 9, which is in the ten millions place, is 9 x 10000000 = 90000000.
Example 4
For the number 183 256 094, write down the place value of each digit.
Answer:
The digit 4, which is in the ones place, is 4 x 1 = 4.
The digit 9, which is in the tens place, is 9 x 10 = 90.
The digit 0, which is in the hundreds place, is 0 x 100 = 0.
The digit 6, which is in the thousands place, is 6 x 1000 = 6000.
The digit 5, which is in the ten thousands place, is 5 x 10000 = 50000.
The digit 2, which is in the hundred thousands place, is 2 x 100000 = 200000.
The digit 3, which is in the millions place, is 3 x 1000000 = 0.
The digit 8, which is in the ten millions place, is 8 x 10000000 = 80000000.
The digit 1, which is in the hundred millions place, is 1 x 100000000 = 100000000.
Example 5
For the number 742 193 568, write down the place value of each digit.
Answer:
The value of the digit 8, which is in the ones place, is 8 x 1 = 8.
The value of the digit 6, which is in the tens place, is 6 x 10 = 60.
The value of the digit 5, which is in the hundreds place, is 5 x 100 = 500.
The value of the digit 3, which is in the thousands place, is 3 x 1000 = 3000.
The value of the digit 9, which is in the ten thousands place, is 9 x 10000 = 90000.
The value of the digit 1, which is in the hundred thousands place, is 1 x 100000 = 100000.
The value of the digit 2, which is in the millions place, is 2 x 1000000 = 0.
The value of the digit 4, which is in the ten millions place, is 4 x 10000000 = 40000000.
The value of the digit 7, which is in the hundred millions place, is 7 x 100000000 = 700000000.
Using Base Ten Blocks to Place Value
We can also write numbers in their expanded form using base-ten blocks to indicate the digit’s place value. The place value system allows for a range of values for each digit, from zero to nine. We re-start at zero but increase the value of the digit in the next highest place value by one when a digit’s value rises past nine. Let’s first learn what these base ten blocks stand for before using them to determine each digit’s place value.
Examples
Example 1:
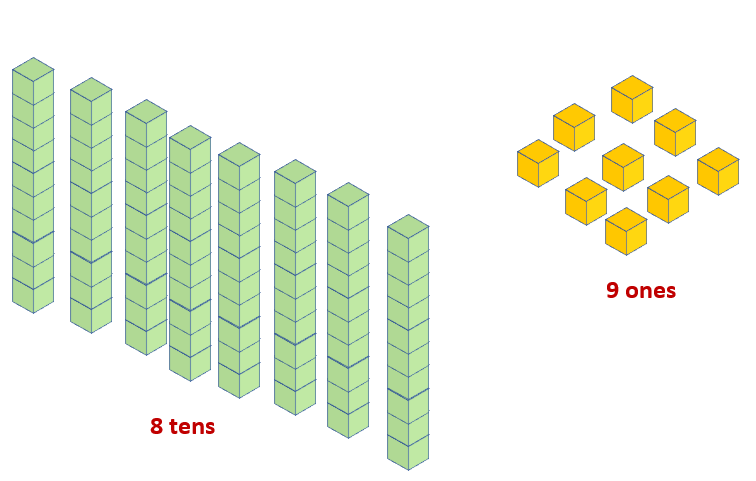
To represent the number 89, use base ten blocks.
Answer:
The value of the digit 9, which is in the ones place, is 9 x 1 = 9.
The value of the digit 8, which is in the tens place, is 8 x 10 = 80.
The illustration below shows the number 89 using base ten blocks.
Example 2:
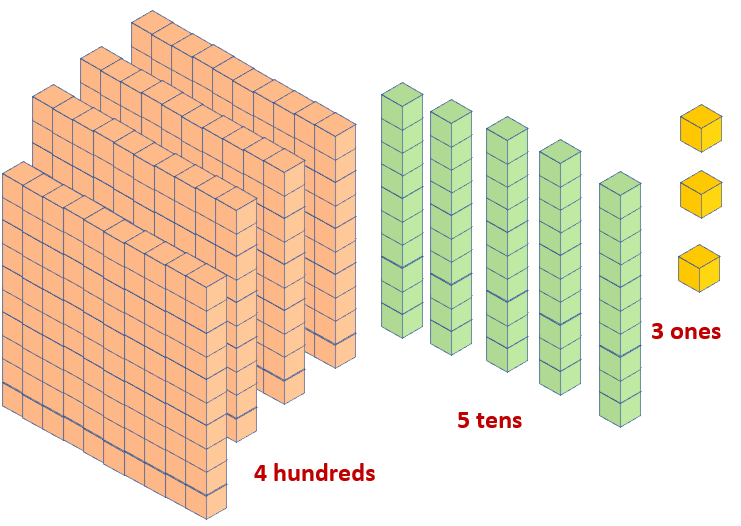
To represent the number 453, use base ten blocks.
Answer:
The value of the digit 3, which is in the ones place, is 3 x 1 = 3.
The value of the digit 5, which is in the tens place, is 5 x 10 = 50.
The value of the digit 4, which is in the hundreds place, is 4 x 100 = 400.
The illustration below shows the number 453 using base ten blocks.
Example 3:
To represent the number 142, use base ten blocks.
Answer:
The value of the digit 2, which is in the ones place, is 2 x 1 = 2.
The value of the digit 4, which is in the tens place, is 4 x 10 = 40.
The value of the digit 1, which is in the hundreds place, is 1 x 100 = 100.
The illustration below shows the number 142 using base ten blocks.
Example 4:
To represent the number 1254, use base ten blocks.
Answer:
The value of the digit 4, which is in the ones place, is 4 x 1 = 4.
The value of the digit 5, which is in the tens place, is 5 x 10 = 50.
The value of the digit 2, which is in the hundreds place, is 2 x 100 = 200.
The value of the digit 1, which is in the thousands place, is 1 x 100 = 1000.
The illustration below shows the number 1254 using base ten blocks.

Examples: Number Change
Now that the concept of place value has been illustrated already let us talk about number change or how a number change if we change a digit.
Number change has something to do with either adding or subtracting from one number to make another number, together with the knowledge of how much to add or subtract.
Example 1
How much does the number 253 change if we take away 1 in the hundreds place?
Solution:
The value of the digit 3, which is in the ones place, is 3 x 1 = 3.
The value of the digit 5, which is in the tens place, is 5 x 10 = 50.
The value of the digit 2, which is in the hundreds place, is 2 x 100 = 200.
If we take away 1 in the hundreds place of the number 253, this means that we are subtracting 100 from 253. Therefore, we have 253 – 100, which is 153. Since we have subtracted 100, 153 is 100 less than 253.
253-100=153
Example 2
How much does the number 678 change if we take away 2 in the tens place?
Solution:
The value of the digit 8, which is in the ones place, is 8 x 1 = 8.
The value of the digit 7, which is in the tens place, is 7 x 10 = 70.
The value of the digit 6, which is in the hundreds place, is 6 x 100 = 600.
Taking away 2 in the tens place of 678 means that we have to subtract 20 from it. Hence, we have 678 – 20. Since we have subtracted 20 from 678, the new number is 658.
678-20=658
Example 3
How much does the number 5967 change if we take away 5 tens?
Solution:
The value of the digit 7, which is in the ones place, is 7 x 1 = 7.
The value of the digit 6, which is in the tens place, is 6 x 10 = 60.
The value of the digit 9, which is in the hundreds, place is 9 x 100 = 900.
The value of the digit 5, which is in the thousands place, is 5 x 1000 = 5000.
If we take away 5 tens from the number 5967, this means that we are subtracting 50 from 5967. Therefore, we have 5967 – 50, which is 5917. Since we have subtracted 50, the 5917 is 50 less than 5967.
5967-50=5917
Example 4
By how much does the number 62583 change if we add 4 hundreds?
Solution:
The value of the digit 3, which is in the ones place, is 3 x 1 = 3.
The value of the digit 8, which is in the tens place, is 8 x 10 = 80.
The value of the digit 5, which is in the hundreds place, is 5 x 100 = 500.
The value of the digit 2, which is in the thousands place, is 2 x 1000 = 2000.
The value of the digit 6, which is in the ten thousands place, is 6 x 10000 = 60000.
If we add 4 hundreds to the number 62583, this means that we are adding 400 to 62583. Thus, we have 62583 + 400, which is 62983.
62583+400=62983
Example 5
By how much does the number 12864 change if we add 7 hundreds?
Solution:
The value of the digit 4, which is in the ones place, is 4 x 1 = 4.
The value of the digit 6, which is in the tens place, is 6 x 10 = 60.
The value of the digit 8, which is in the hundreds place, is 8 x 100 = 800.
The value of the digit 2, which is in the thousands place, is 2 x 1000 = 2000.
The value of the digit 1, which is in the ten thousands place, is 1 x 10000 = 10000.
Adding 7 hundreds means adding 700 to the given number. Therefore we have 12864 + 700. Looking at the hundreds place, 800 + 700 is equal to 1500. This means we have 5 hundreds and add 1 to the thousands place. Since we need to add the whole 1 thousand to the number, the digit 2 in the thousands place will be 3. Hence, the new number is 13564.
12864+700=13564
Example 6
By how much does the number 678298 change if we add 5 thousands?
Solution:
The value of the digit 8, which is in the ones place, is 8 x 1 = 8.
The value of the digit 9, which is in the tens place, is 9 x 10 = 90.
The value of the digit 2, which is in the hundreds place, is 2 x 100 = 200.
The value of the digit 8, which is in the thousands place, is 8 x 1000 = 8000.
The value of the digit 7, which is in the ten thousands place, is 7 x 10000 = 70000.
The value of the digit 6, which is in the hundred thousands place, is 6 x 100000 = 600000.
Adding 5 thousands means adding 5000 to the given number. Thus, we have 678298 + 5000. Since the value in the thousands place is 8000 and we need to add 5000 to it, we have a total of 1300. This means that we have 3 in the hundreds place and add 1 to the ten thousands place. Since we need to add the whole 1 ten thousand to the number, then the digit 7 in the ten thousands place will be 8. Hence, the new number is 683298.
678298 +5000=683298
Example 7
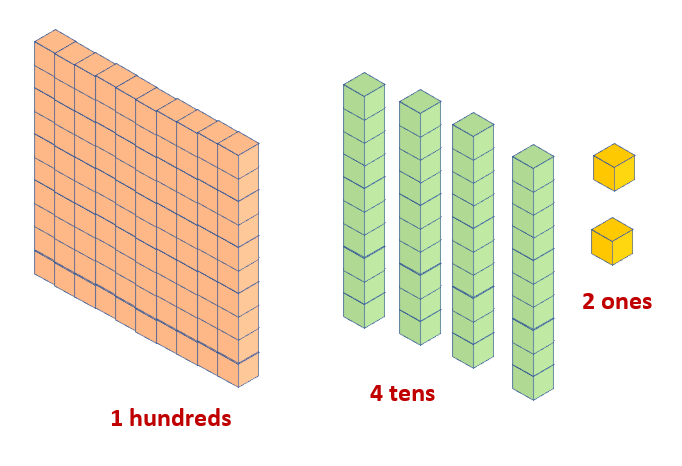
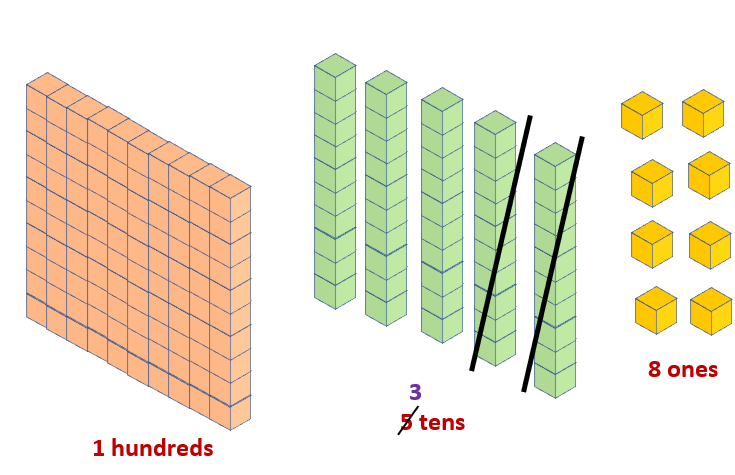
Using number blocks, show how much the number 158 changes if we take away 2 tens?
Solution:
The value of the digit 8, which is in the ones place, is 8 x 1 = 8.
The value of the digit 5, which is in the tens place, is 5 x 10 = 50.
The value of the digit 1, which is in the hundreds place, is 1 x 100 = 100.
If we take away 2 tens from the number 158, this means that we are subtracting 20 from 158. Therefore, we have 158 – 20, which is 138. Since we have subtracted 20, the 138 is 20 less than 158.
158-20=138
Example 8
Using number blocks, show how much the number 3149 changes if we take away 2 thousands?
Solution:
The value of the digit 9, which is in the ones place, is 9 x 1 = 9.
The value of the digit 4, which is in the tens place, is 4 x 10 = 40.
The value of the digit 1, which is in the hundreds place, is 1 x 100 = 100.
The value of the digit 3, which is in the thousands place, is 3 x 1000 = 3000.
If we take away 2 thousands from the number 3149, this means that we are subtracting 2000 from 3149. Therefore, we have 3149 – 2000, which is 1149. Since we have subtracted 2000, the number 1149 is 2000 less than 3149.
3149-2000=1149
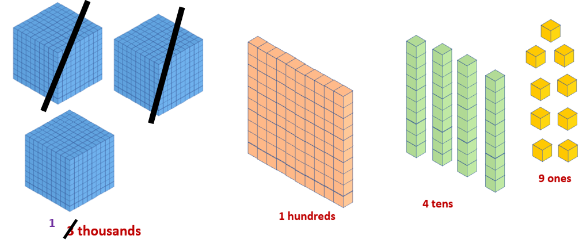
Example 8
Show how much the number 7286 changes if we add 2 hundreds.
Solution:
The value of the digit 6, which is in the ones place, is 6 x 1 = 6.
The value of the digit 8, which is in the tens place, is 8 x 10 = 80.
The value of the digit 2, which is in the hundreds place, is 2 x 100 = 200.
The value of the digit 7, which is in the thousands place, is 7 x 1000 = 7000.
If we add 2 hundreds to the number 7286, this means that we are adding 200 to 7286. Therefore, we have 7286 + 200, which is 7486. Since we have added 200, the number 7486 is 300 greater than 7286.
7286-200=7486
Summary
- The value a digit in a number represents based on where it is in the number is known as place value.
- The placement of each digit represents value. These positions begin at the unit place, often known as the ones position. Ones/unit, tens, hundreds, thousands, ten thousand, one hundred thousand, and so on are the place values of a number’s digits from right to left.
- An illustration that enables us to locate and contrast the place values of the digits in numbers up to millions is known as a place value chart. As we move from left to right on the place value chart, a digit’s place value goes up by ten times and down by ten times.
- A one-digit number has a place value equal to its face value.
- Any number’s place value for zero is always zero. Zero may appear anywhere in a number, but it will always have zero value.
- The place value system allows for a range of values for each digit, from zero to nine. We re-start at zero but increase the value of the digit in the next highest place value by one when a digit’s value rises past nine.
Recommended Worksheets
Place Value (International Children’s Day Themed) Math Worksheets
Understanding Tens and Ones 1st Grade Math Worksheets
Real Numbers (World Meteorological Day Themed) Math Worksheets









