What is the use of function tables in coordinate graphing?
Many situations in our lives involve two sets of numbers that are related to one another. For example, if you know the cost of one ticket to a movie show, you can calculate the total cost for any number of people who will watch it. Likewise, if you know how much a certain fruit costs per kilogram, then you can calculate how many kilograms you can purchase with the amount of money you have in your wallet.
Most of the time, the most challenging part of figuring out a complicated problem is keeping all the data organized so you will not lose track during the process of problem-solving. The use of a function table or “T-chart” can come in handy when organizing data because it shows the relationship between two different strings of numbers. Each function table contains a rule known as “function,” which generates a pattern for one string of numbers (often designated by the dependent variable y) when another string of numbers (often designated by the independent variable “x”) is used.
The examples below will demonstrate how a function table can be used to calculate how much it would cost for the “x” number of people to watch a \$5 per person afternoon movie.
Let us use “x” as a placeholder for the unknown value to enable us to generalize information and to write a function or rule that will work for any number of people who will attend to watch the afternoon movie. We can determine the corresponding value for y by plugging in a value for x in the function of the given mathematical real-life problem. In this respect, y is the total cost of tickets for those who are going to watch the afternoon movie.
So, let x = the number of people who will watch the afternoon movie
y = the total cost of tickets of those who are going to watch the afternoon movie
Since we know that each ticket costs \$5, our working functional equation would be 5x = y. Thus, start plugging in the values for x in the equation, one at a time.
| x | 5x = y | y | This means… |
| 1 | 5 (1) = y | 5 | \$5 x 1 person = \$5 |
| 2 | 5 (2) = y | 10 | \$5 x 2 persons = \$10 |
| 3 | 5 (3) =y | 15 | \$5 x 3 persons = \$15 |
| 4 | 5 (4) =y | 20 | \$5 x 4 persons = \$20 |
| 5 | 5 (5) =y | 25 | \$5 x 5 persons = \$25 |
Suppose the evening movie show costs \$9, we could make another table just like below.
| x | 9x = y | y | This means… |
| 1 | 9 (1) = y | 9 | \$9 x 1 person = \$9 |
| 2 | 9 (2) = y | 18 | \$9 x 2 person = \$18 |
| 3 | 9 (3) =y | 27 | \$9 x 3 person = \$27 |
| 4 | 9 (4) =y | 36 | \$9 x 4 person = \$36 |
| 5 | 9 (5) =y | 45 | \$9 x 5 person = \$45 |
Be reminded that the values of x and y, which are on the same row on the function table, are related to each other, and their relationship is defined by the functional equation 5x = y. Sometimes it can become confusing for some people because they mistakenly try to match numbers that are not on the same row and thus unrelated to each other on the function table.
While creating a function table is a helpful technique for some problems which involve small numbers like figuring out the total cost of tickets of a group of people that will watch a movie together, their real significance can be seen when we apply the patterns to large numbers. Problems that involve small numbers typically have many ways to be solved, such as using pictures, drawing diagrams, or tallying marks. We know that numbers can be added repeatedly but, no one would want to draw 326 pictures of something, or make multiple diagrams of something, or count out 2,352 tally marks just to solve a problem. Even though it is possible, but it is inefficient. Hence, understanding a pattern that deals with small numbers is essential because the same pattern can also be utilized to help you work out much larger numbers.
Each corresponding pair of numbers on the same row of the function table is used to write an ordered pair. In graphing an ordered pair, we always start at the origin. Then, we either move to the right of the x-axis if the value of x is positive, or we move to the left of the x-axis if the value of x is negative. From there, we either move up the y- axis if the value of y is positive, or we move down the y- axis if the value of y is negative.
How to use coordinate planes in problem-solving?
We can also use coordinate planes to describe how one quantity is related to another. By determining the independent variable x and the dependent variable y, we can use a coordinate plane to describe any mathematical relationship. For example, if our independent variable x is the price of an item and the dependent variable y is the number of items you sell, we can create a graph in the coordinate plane to help us understand the relationship of these quantities. We can apply this to a huge range of different problems because the coordinate plane allows us to see how one quantity varies with another in a visual way.
How to solve real-world problems by coordinate graphing?
Graphs play an important role in mathematics and work as very useful tools even in real life. These ways of visual representation of numeric data are an easy and less complicated way to read data. The use of graphs in representing lengthy data saves time in analyzing data and in gaining quick insights. Reading graphical data is easy as compared to lengthy reports, and it saves time in preparing detailed documentation. Results that may take up two to three pages of a report can be represented easily in one or even half of a page. It is an effective tool in representing the sales statistics of a business, can even help in accurately displaying medical data that is easy and simple to understand.
Let us use a coordinate graph to show real-world situations involving related numbers. We will also be looking at the information displayed on a coordinate graph and understanding the real-world situation that it describes.
Example 1
Suppose you read two books per day. Show the relationship between the number of books you read and the number of days you read.
First, let us create our function table.
Let x = the number of days
y = the number of books you read
Since we know that you read two books per day, our working functional equation would be y = 2x. So, let us plug in the values for x in the equation, one at a time.
| x | y = 2x | y | Ordered Pair |
| 1 | y = 2 (1) | 2 | (1, 2) |
| 2 | y = 2 (2) | 4 | (2, 4) |
| 3 | y = 2 (3) | 6 | (3, 6) |
| 4 | y = 2 (4) | 8 | (4, 8) |
| 5 | y = 2 (5) | 10 | (5, 10) |
Now, let us create a graph using the ordered pairs formed from our x and y values in our function table.
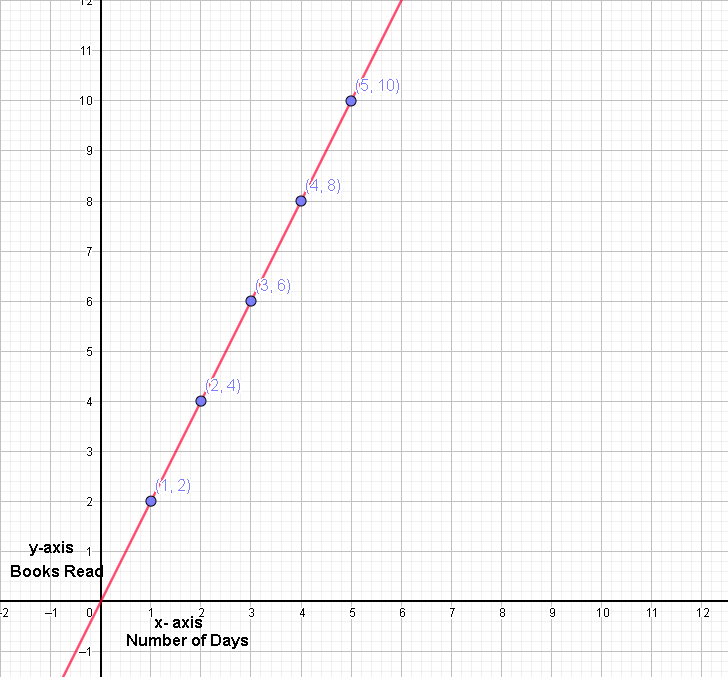
Notice how the graph helps us easily see that the number of books you read increases as the number of days you spend reading.
Example 2
Suppose a pizza shop sells a small pizza for \$5, and each topping costs \$1. Show the relationship between the number of toppings in a pizza and the cost of the pizza.
First, let us create our function table.
Let x = the number of toppings
y = the cost of pizza
Since we know that a small pizza costs \$5 and each topping costs \$1, our working functional equation would be y = 5 + 2x. So, let us plug in the values for x in the equation, one at a time.
| x | y = 5 + 2x | y | Ordered Pair |
| 1 | y = 5 + 2 (1) | 7 | (1, 7) |
| 2 | y = 5 + 2 (2) | 9 | (2, 9) |
| 3 | y = 5 + 2 (3) | 11 | (3, 11) |
| 4 | y = 5 + 2 (4) | 13 | (4, 13) |
| 5 | y = 5 + 2 (5) | 15 | (5, 15) |
Now, let us create a graph using the ordered pairs formed from our x and y values in our function table.
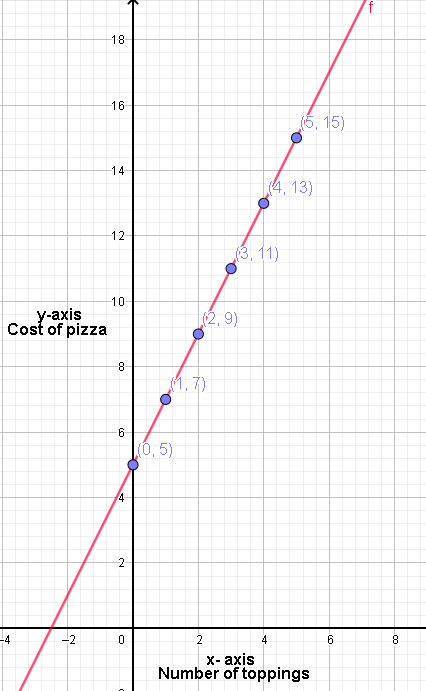
Notice that even we did not include 0 to be one of our x values in the function table, the graph shows that you will only pay \$5 when we buy a pizza with no toppings. The graph also shows that the cost of a small pizza increases as we add more toppings.
Example 3
Kim is drinking a soda in a can as fast as she can. The amount of soda left in the can (in milliliters) as a function of time (in seconds) is graphed below. What can you infer from the graph?
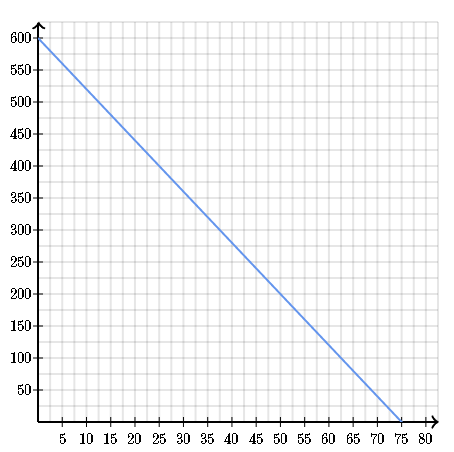
Notice that the graph is falling from left to right. Thus, it has a negative slope. This suggests that as one quantity increases, the other decreases. In this case, while Kim is consuming the soda every second, the amount of soda in the can decreases.
We can also infer from the graph that the can contains 600 milliliters of soda because 600 is the y- value when the x- value is 0 (0 seconds means the soda in the can is still full). In addition, we can say that Kim emptied the soda can after 75 seconds because 75 is the x- value when the y- value is 0 (0 milliliters means the soda can is empty).
Example 4
Below is a graph that shows a 500-liter oil tank that is being drained at the constant rate of 20 liters per minute. At what time would the water tank be emptied?
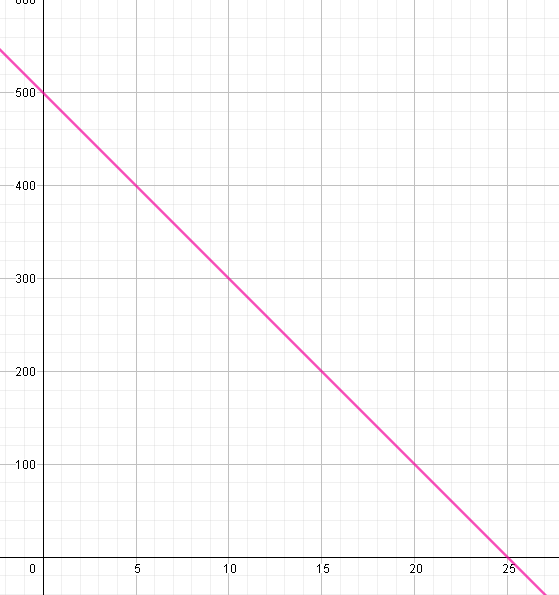
Notice that the graph is falling from left to right. Thus, it has a negative slope. This suggests that as one quantity increases, the other decreases. In this case, while the oil tank is draining every minute, the amount of oil in the tank decreases.
We can also infer from the graph that the oil tank is emptied after 25 minutes.
Example 5
Suppose y (in decimal form) is the battery power percentage remaining x hours after a laptop computer is turned on and that y = −0.2 x + 1. (a) Graph the equation. (b) Interpret the x- and y-intercepts. (c) Find how many hours after will the battery power be at 60%.
- Use the slope and the y-intercept to graph the equation
The equation y = −0.2 x + 1 tells us that its graph has a slope of −0.2 and a y-intercept of 1. So, plot (0, 1) first and use the slope to plot another point on the graph, say (1, 0.8). Draw a line by connecting the plotted points.
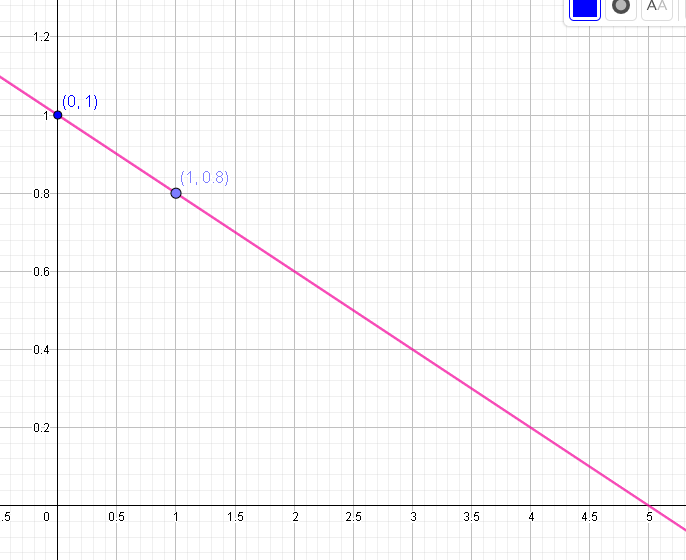
- To find the x-intercept, we must substitute 0 as a value for y in the equation.
y = −0.2x + 1
0 = −0.2x + 1
5 = x
The x-intercept is 5, which can also be seen in the graph above. This means that the battery can last up to 5 hours. The y-intercept is which means that the battery power was at 100% when the laptop was turned on.
- Find the value of x when y = 0.60
We can answer this by either working with the given equation or by simply looking at the graph.
If we intend to use the equation, we can substitute 0.60 as the value of y and then solve for x.
y = − 0.2x + 1
0.60 = − 0.2x + 1
0.60 − 1 = − 0.2x
0.2x = 1− 0.60
0.2x = 0. 40
x = 2
If we use the graph to answer the given question, we look for the corresponding value of x if our y is at 0.6.
Thus, the battery percentage of the laptop will be at 60% after 2 hours.
Example 6
The graph represents the height y (in feet) of a flag x seconds after it was raised up on a flagpole. (a) Find and interpret the slope. (b) Find and interpret the y-intercept (c) What is the height of the flag after 6 seconds?
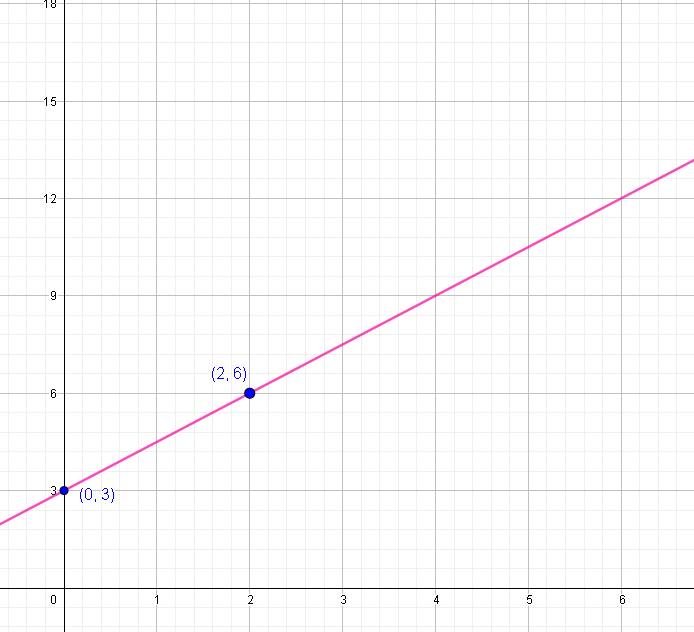
- Find and interpret the slope.
The slope is 32. This means that the height of the flag will be 3 feet more every 2 seconds.
- Find and interpret the y-intercept.
The graph crosses the y- axis at point (0, 3), so the y-intercept is 3. This means that the flag was 3 feet high before it was raised up.
- What is the height of the flag after 6 seconds?
Looking at the corresponding value of y in the graph when the value of x is equal to 6, we can say that the flag is 12 feet high after 6 seconds.
What is the importance of graphing in our lives?
We humans have taken too much work to get our jobs done for too long. It is time to simplify our lives and use the best tools for us to be more efficient when working on something. Graphing is one of those tools that we must have. Graphs are almost everywhere and are used in our daily life, from the local newspaper to the bookstores. It is one of the essential skills that we must acquire. If used appropriately, a graph can help us and make our lives easier.
As we all know, graphs are planned drawing which consists of lines and numbers that are related to one another. With all the technology that we now have, we can quickly create a professional-looking graph in no time with the use of colors and a little imagination.
Graphing is not just for those who do extremely well in math but for everyone to use it according to their needs. So, we need the basic knowledge of making use of graphs when doing calculations in our daily lives.
A graph can help you evaluate calculations more effectively. For example, planning our monthly budget can benefit from creating a graph. Doing this for a couple of months will help us see where we make mistakes and where we succeed in terms of budgeting. Another example is when measuring seismic waves; using a graph can help in identifying any faulty areas and help in keeping track of the situation. When conducting a survey, creating a graph can be used to present a huge amount of information that needs to be assessed and interpreted in a single figure. In addition, managers, or sales assistants, also made use of graphs if they need to know why and how to correct some mistakes when they have not met their monthly targets. Accountants also benefit from sing graphs to convey financial information to their clients. A graph can be very handy because it can be a place where you store all the data you have collected.
Graphs can be very effective tools for quickly presenting visual information. A graph can be used by almost anyone because it is easy to draw. A few dots, lines, and a little bit of knowledge about graphing can go a long way.
Recommended Worksheets
Graphing Points on the Coordinate Plane 5th Grade Math Worksheets
Graphing and Solving Systems of Linear Equations in Two Variables 8th Grade Math Worksheets
Number Lines and Coordinate Planes 6th Grade Math Worksheets









