What is a straight line?

A straight line is a curve such that every point on the line segment joining any two points on it lies on it.

Let ax + by + c = 0 be a first degree equation in x, y where a, b, c are constants. Let P (x₁, y₁) and Q(x₂, y₂) be any point on the curve represented by ax+ by + c = 0. Then,

ax₁ + by₁ + c = 0 and ax₂ + by² + c = 0

When we say that the first degree equation is x, i.e. ax + by + c = 0 represents a line, it means that all points (x, y) satisfying ax + by + c = 0 lie along a line. Thus, a line is also defined as the locus of a point satisfying the condition ax + by + c = 0, where a, b, c are constants.   

It should be noted that there are only two unknowns in the equation of a straight line because the equation of every straight line can be put in the form ax + by + c = 0, where a and b are two unknowns. It is important to note here that x and y are not unknowns.  In fact, these are the coordinates of any point on the line and are known as current coordinates. Thus, to determine a line we will need two coordinates to determine the two unknowns.

Slope of a Line

The trigonometrical tangent of the angle that a line makes with the positive direction of the x-axis in an anticlockwise sense is called the slope or the gradient of a line.

The slope of a line is generally denoted by m. Thus m = $\tan \Theta$

Since a line parallel to the x-axis makes an angle of 0^o with the x-axis, therefore, its slope is tan 0⁰ = 0

A line parallel to the y-axis, i.e. a line that is perpendicular to the x-axis makes an angle of 90^o with the x-axis, so its slope is tan $\frac{\pi }{2}$ = ∞. Also, the slope of a line equally inclined with axes is 1 or -1 as it makes an angle of 45^o or 135^o with the x-axis.

 The angle of inclination of a line with the positive direction of the x-axis in an anticlockwise sense always lies between 0⁰ and 180⁰.

Let us now understand the slop using some examples.

Example

What can be said regarding a line is its slope is a) positive b) zero c) negative?

Solution

Let $\Theta$ be the angle of inclination of the given line with the positive direction of the x-axis in an anticlockwise sense.  Then, its slope is given by m = tan $\Theta$.

a)            If the slope of the line is positive, then,

                m = tan $\Theta$ > 0 ⇒ $\Theta$ lies between 0⁰ and 90⁰

This means that $\Theta$ is an acute angle.

Thus the line of positive slope makes an acute angle with the parallel direction of the x-axis.

b)            If the slope of a line is zero, then,

                m = tan $\Theta$ = 0 ⇒ $\Theta$ = 0⁰

                This means that either the line is x-axis or it is parallel to the x-axis.

Thus the line of zero slope is parallel to the x-axis.

c)            If the slope of the line is negative, then,

m = tan $\Theta$ < 0 ⇒ $\Theta$ lies between 90⁰ and 180⁰

This means that $\Theta$ is an obtuse angle.

Thus the line of negative slope makes an obtuse angle with the parallel direction of the x-axis in an anticlockwise direction.

Slope of a line in Terms of Coordinates of any Two Points on it

What would be the slope of a line in terms of coordinates of any two points on it? Let us find out.

Let P(x₁, y₁) and Q(x₂, y₂) be two points on a line making an angle q with the positive direction of the x-axis. Draw Pl, QM perpendicular on x-axis and PN_QN on QM. Then,

PN = LM = OM – OL = x₂ – x₁ and QN = QM – NM = QM – PL = y₂ – y₁

In △ PQN, we have,

tan  $\Theta =\frac{QN}{PN}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

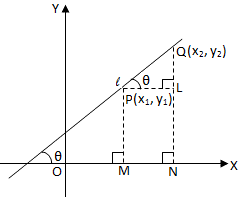
Thus, if (x₁, y₁) and (x₂, y₂) are coordinates of any two points on a line then its slope is given by

m =  $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{Difference\, in\, ordinates}{Difference\, in \, adbscissae}$

Let us understand it through an example.

Example

Find the slope of a line that passes through the points (3, 2) and (-1, 5)

Solution

We know that the slope of a line passing through two points (x₁, y₁) and (x₂, y₂) is given by

m = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

Here, y₁ = 2, y₂ = 6, x₁ = 3, x₂ = -1

Substituting these values in the given equation, we have

m = $\frac{5-2}{-1-3}=\frac{-3}{4}$

Hence, the slope of a line that passes through the points (3, 2) and (-1, 5) is $\frac{-3}{4}$.

Point-Slope Form

The equation of a straight line can be written in different forms depending on the data give. One of such forms is the point-slope form. The point-slope form includes the slope of the straight line and a point on the line as the name suggests. There can be infinite lines with a given slope, but when we specify that the line passes through a given point then we get a unique straight line. Thus, only a point on the line and its slope are required to represent a straight line in the point-slope form. Let us now understand what is a point-slope form?

The theorem of the point-slope form states that:

The equation of a line that passes through the point (x₁, y₁) and has the slope “m” is given by:

y – y₁ = m (x – x₁)

How did we reach upon this formula? Let us check out.

Let the straight line passing through the point Q(x₁, y₁) and let P (x, y) be any point on the line.

Then, we know that the Slope of a line = $\frac{y-y_{1}}{x-x_{1}}$

But, we also know that the slope of the line is “m”

Therefore,

 m = $frac{y-y_{1}}{x-x_{1}}$

⇒  $y-y_{1}=m(x-x_{1})$

Hence, $y-y_{1}=m(x-x_{1})$ is the required equation of the line.

Solving Point-Slope Form Equation

The following steps should be followed for finding the equation of a given line of for solving the point-slope form:

1. Make a note of the coordinate values of (x₁, y₁) and the value of m of the straight line.
2. In the formula, $y-y_{1}=m(x-x_{1})$, substitute the values given.
3. Simplify the equation to obtain the standard form of the equation.

Solved Examples

Example 1   

Find the equation of a line passing through (2, -3) and inclined at an angle of 135^o with the positive direction of the x-axis.

Solution              

To find the equation first we need to find the slope of the line using the given inclination.

We have been given that

m = Slope of the line = tan 135^o

Now we can write tan 135^o as tan (90^o + 45^o)

Further, tan (90^o + 45^o) = -cot 45^o = -1 ( because tan (90 + q) = -cot q and cot 45^o = 1)

Also, we have bene given that x₁ = 2 and y₁ = -3

Now, we know that the equation of the line in point-slope forms I

$y-y_{1}=m(x-x_{1})$

Substituting the given values in the above equation, we have

$y-(-3)=-1(x-2)$

y + 3 = -x + 2

⇒ x + y +1 = 0

Hence, the equation of a line passing through (2, -3) and inclined at an angle of 135^o with the positive direction of the x-axis will be x + y +1 = 0

Example 2    

Determine the equation of the line through the point (4, -3) and parallel axis.

Solution              

We have been given that the straight line passes through the point ( 4, -3 ).

This means we have been given that x₁ = 4 and y₁ =  -3

Also, the straight line is parallel to the x-axis.

Now, recall that we have learnt that the line of zero slope is parallel to the x-axis. This means that is a line is parallel to the axis if the slope of a line is zero, or,

m = tan $\Theta$ = 0 ⇒ $\Theta$ = 0⁰

So, we have m = 0

We also know that,

Now, we know that the equation of the line in point-slope forms I

 $y-y_{1}=m(x-x_{1})$

Substituting the given values in the above equation, we have

 $y-(-3)=0(x-2)$

⇒ y  + 3 = 0

Hence, the equation of the line through the point (4, -3) and parallel axis will be given by y  + 3 = 0

Example 3    

Find the equation of a straight line passing through (-9, 5) and inclined at an angle of 120° with the positive direction of the x-axis.

Solution          

To find the equation first we need to find the slope of the line using the given inclination.

We have been given that slope of the line (m) = tan 120°

Now we can write tan 120° as tan (90° + 30°) = cot 30° = -√3. ( because tan (90 + q) = -cot q and cot 30^o = √3)

Also, we have bene given that x₁ = -9 and y₁ =  5

Now, we know that the equation of the line in point-slope forms I

$y-y_{1}=m(x-x_{1})$

Substituting the given values in the above equation, we have

Therefore, the required equation of the straight line is

 = $y-(-5)=-\sqrt{3}(x-(-9))$

⇒ y – 5 = -√3 ( x+ 9 )

⇒ y – 5 = -√3x –  9√3

 ⇒ y + √3x + 9√3 – 5 = 0

Hence, the equation of a straight line passing through (-9, 5) and inclined at an angle of 120° with the positive direction of the x-axis will be y + √3x + 9√3 – 5 = 0

Example 4    

Find the equation of the straight line with slope 3 and passing through (-1, 5).

Solution          

We have been given that the slope of the line is 3 or m = 3 and the line passes through (-1, 5),

We have also been given that  (x₁, y₁) = (-1, 5). This means that x₁ = -1 and y₁ = 5

Now, we know that the equation of the line in point-slope forms I

$y-y_{1}=m(x-x_{1})$

Substituting the given values in the above equation, we have

Therefore, the required equation of the straight line is

$y-5=3(x-(-1))$

y – 5 =  3 ( x  + 1 )

y – 5 = 3x + 3

⇒ 3x – y + 8 = 0

Hence, the equation of the straight line with slope 3 and passing through (-1, 5) will be given by 3x – y + 8 = 0

Example 5    

Find the equation of the straight line with slope -2 and passing through (7, -4).

Solution          

We have been given that the slope of the line is 2 or m = -2 and the line passes through ( 7, -4 ),

We have also been given that  (x₁, y₁) = ( 7, -4) . This means that x₁ = 7 and y₁ = -4

Now, we know that the equation of the line in point-slope form is

$y-y_{1}=m(x-x_{1})$

Substituting the given values in the above equation, we have

Therefore, the required equation of the straight line is

$y-(-4)=-2(x-7)$

 y + 4 = -2x + 14

⇒ 2x – y + 10 = 0

Hence, the equation of the straight line with slope -2 and passing through (7, -4) is 2x – y + 10 = 0

Example 6    

Find the equation of the perpendicular bisector of the line segment joining the points A (2, 3) and B (6, -5 ).

Solution              

To find the equation first we need to find the slope of the line

Recall that if (x₁, y₁) and (x₂, y₂) are coordinates of any two points on a line then its slope is given by

m = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

We have been given that x₁ = 2 and y₁ = 3. Also x₂ = 6 and y₂ = – 5

Substituting these values in the above equation we will get

m =  $\frac{-5-3}{6-2}=\frac{-8}{4}=-2$

Now, we know that the slope of a line perpendicular to the line AB will be given by $\frac{-1}{m}$.

Therefore, we have

Slope of the line = $\frac{1}{2}$

Now, let P be the mid-point of AB. Then the coordinates of P will be given by

$(\frac{2+6}{2},\frac{3-5}{2})=( 4, -1 )$

Since now we have one point as well as the slope of the line, we can use the point-slope form to find the equation of the line.

We know that the equation of the line in point-slope form is

$$

Substituting the given values in the above equation, we have

Therefore, the required equation of the straight line is

$\frac{y-y_{1}}{x-x_{1}}$

$y+1=\frac{1}{2}(x-4)$

⇒ 2 ( y + 1 ) = 1 ( x – 4 )

⇒ 2y + 2 = x – 4

⇒ x – 2y – 6 = 0

Hence, the equation of the perpendicular bisector of the line segment joining the points A (2, 3) and B (6, -5 ) will be given by x – 2y – 6 = 0

Example 7    

A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1:2. Find the equation of the line.

Solution              

We have been given that the points are(1, 0) and (2, 3) and the line perpendicular to the line segment divides it in the ratio of 1 : 2.

 Let M divide the join of A(1,0) and B(2,3) in the ratio of 1:2

Then, the point M is $(\frac{1\times 2+2\times 1}{1+2},\frac{1\times 3+2\times 0}{1+2})$.

Hence, M= $(\frac{4}{3},1)$

Slope of the line AB= $\frac{3-0}{2-1}$ = 3

Let L be the required line. Then, the slope of L= $\frac{-1}{3}$ and it passes through M.

Now, let L be the required line. we have been given that L is perpendicular to AB.

Therefore,

Slope of L= $\frac{-1}{3}$ and it passes through M $(\frac{4}{3},1)$

Since now we have one point as well as the slope of the line, we can use the point-slope form to find the equation of the line.

We know that the equation of the line in point-slope form is

 $y-y_{1}=m(x-x_{1})$

Substituting the given values in the above equation, we have

Therefore, the required equation of the straight line is

$y-1=\frac{-1}{3}(x-\frac{4}{3})$

 9 ( y – 1 ) = -1 ( 3x – 4 )

⇒ 9y – 9 = -3x + 4

⇒ 3x + 9y – 13 = 0

Hence, the equation of the line that is perpendicular to the line segment joining the points (1, 0) and ( 2, 3 ) and divides it in the ratio 1:2 will be given by 3x + 9y – 13 = 0

Remember

1. A straight line is a curve such that every point on the line segment joining any two points on it lies on it.
2. To determine a line we will need two coordinates to determine the two unknowns.
3. The trigonometrical tangent of the angle that a line makes with the positive direction of the x-axis in an anticlockwise sense is called the slope or the gradient of a line.
4. The slope of a line is generally denoted by m. Thus m = tan$\Theta$
5. Thus the line of positive slope makes an acute angle with the parallel direction of the x-axis.
6. Thus the line of negative slope makes an obtuse angle with the parallel direction of the x-axis in an anticlockwise direction.
7. Thus the line of zero slope is parallel to the x-axis
8. The point-slope form includes the slope of the straight line and a point on the line
9. Thus, if (x₁, y₁) and (x₂, y₂) are coordinates of any two points on a line then its slope is given by m = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{Difference\, in\, ordinates}{Difference\, in \, adbscissae}$
10. The equation of a line that passes through the point (x₁, y₁) and has the slope “m” is given by: y – y₁ = m (x – x₁)

Recommended Worksheets

Dot Plots/Line Plots with Fractional Units (Snacks and Beverages Themed) Math Worksheets
Line Plots (Logistics Themed) Worksheets
Points and Lines (Stationery Themed) Worksheets