Introduction
Factorization, also known as factoring, is a key mathematical operation that allows us to express a number or an expression as a product of other numbers or expressions. This fundamental concept can unlock complex problems by making them
more straightforward. It’s like breaking down a large puzzle into smaller, more manageable pieces.
Grade Appropriateness
Factorization is typically introduced in the upper elementary grades, around 4th or 5th grade, and remains relevant throughout middle and high school. For our younger readers, you may have already encountered factorization when learning multiplication facts!
Math Domain
Factorization belongs to the domain of Number Theory in mathematics. Number Theory involves the study of properties and relationships of numbers, particularly integers. However, factorization also plays a significant role in Algebra, where it is used to simplify and solve equations.
Applicable Common Core Standards
The Common Core Standards related to factorization include:
4.OA.B.4: Find all factor pairs for a whole number in the range 1-100.
6.NS.B.4: Find the greatest common factor of two whole numbers and use it to express the sum of the two numbers.
7.RP.A.2: Understand that rewriting an expression in different forms sheds light on the problem and its related quantities.
Definition of the Topic
In mathematics, factorization is the process of decomposing a number, polynomial, or other mathematical object into a product of other objects or factors that, when multiplied together, give the original. For example, the number 15 can be factored into 3 and 5, as 3×5 = 15. Similarly, the polynomial x2– 4 can be factored into (x – 2)(x + 2).
Key Concepts
Factors: The numbers you multiply together to get another number are known as factors. For instance, 4 and 5 are factors of 20, while 3 and 6 are factors of 18.
Prime Numbers: A prime number is a number greater than one whose only factors are one and itself. For instance, 2, 3, 5, and 7 are prime numbers.
Greatest Common Factor (GCF): The GCF of two numbers is the largest number that divides both of them without leaving a remainder.
Prime Factorization is the process of expressing or writing a number with primes numbers as its factors. For instance, the prime factorization of 18 is 2×3×3.
Discussion with Illustrative Examples
Factorization is the process of decomposing a number, polynomial, or another mathematical object into a product of other objects or factors that when multiplied together, give the original. It usually results in simpler or smaller expressions that are always equivalent to its more complicated form.
Factors of Natural Numbers
Let us say we have the natural number 20 and express it as a product of other natural numbers. We shall have,
2×10=20
4×5=20
1×20=20
1, 2, 4, 5, 10, and 20 are the factors of 20. From the list, 2 and 5 are the prime factors of 20. If we write 20 in its prime factor form, we have 2×2×5.
Prime Factorization
Prime factorization is a method of expressing or writing a number as a product of its prime numbers. All prime numbers have only two factors: 1 and itself. For example, 2, 3, 5, 7, 11, 17, 19, 23, and 29 are prime numbers.
The most common methods used for prime factorization are the factor tree and division methods. For example, below are the prime factors of 100 using each method.

Therefore, the prime factors of 100 are 2 and 5, while its prime factorization is 2×2×5×5.
Factors of Algebraic Expressions
Algebraic expressions can be formed as products of factors. Say, for example, the algebraic expression 2ab+3c has two terms, 2ab and 3c, which have the following factors:
2ab=2×a× b
3c=3×c.
Notice that each term cannot be further expressed as a product of factors; hence we may say that 2, a, and b are prime factors of 2ab while 3 and c are the prime factors of 3c.
Suppose we have the expression 2x(x+3). It can be expressed as the product of 2, x, and (x+3) that is 2×x×x+3=2xx+3.
The following are the methods to factorize algebraic expressions.
Factorization by common factors
Factorization by regrouping terms
Factorization using identities
Factors of the form (x+a) (x+b)
Factorization by Common Factors
Common monomial factoring is the process of expressing a polynomial as the product of two polynomials, where one is a monomial that factors each term of the polynomial.
Let us say we have the algebraic expression 3x+15. The following are the factors of each term.
3x=3×x
15=3×5
Hence, we have,
3x+15=(3×x)+(x+5)
Notice that both terms have a common factor which is 3. Therefore, the factors are 3 and (x+5).
3x+15=3 (x+5)
Use the distributive property to check if common monomial factoring is done correctly. The product should be the original expression.
Factorization by Regrouping Terms
Suppose we have the expression 3ab+3a+2b+2. Notice that there is no common factor to all the terms, but 3ab+3a have common factors 3 and a, while 2b+2 have a common factor which is 2.
3ab+3a=(3×a×b)+(3×a)
3ab+3a=(3×a)[b+(1)]
3ab+3a=(3a)(b+1)
2b+2=(2×b)+2
2b+2=2 (b+1)
Therefore, we have the common factor (b+1).
3ab+3a+2b+2=(3a)(b+1)+2 (b+1)
3ab+3a+2b+2=(b+1)(3a+2)
Hence, the factors are (b+1) and (3a+2).
Factoring Using Identities
We can use the following common identities to factorize a given expression.
(x+y)2=x2+2xy+y2
(x-y)2=x2-2xy+y2
x2-y2=(x+y)(x-y)
Let us say we have the expression x2+6x+9. Notice that x2 and 9 are perfect squares, and the middle term is positive (two times the product of the square root of x2 and 9). Hence, it fits the identity (x+y)2=x2+2xy+y2 where x=x and y=3.
x2+6x+9=x2+(2)(x)(3)+32
x2+6x+9=(x+3)2
Factors of the Form (x+a)(x+b)
Some expressions are not of the same form as the identities mentioned earlier. For example, x2+4x+3, m2+5m+6, and d2+9d+14, etc. To factorize these expressions, we follow:
x2+(a+b) x+ab=(x+a)(x+b)
Let us say we want to find the factors of x2+8x+15. Here, ab=15 and a+b=8.
To find the values of a and b, we must consider the factors of 6 when added, which shall result in 8.
So we have 5×3=15 and 5+3=8.
x2+8x+15=x2+(5+3) x+15
x2+8x+15=x2+5x+3x+15
x2+8x+15=(x20+5x)+(3x+15)
x2+8x+15=x(x+5)+3(x+5)
x2+8x+15=(x+5)(x+3)
Examples with Solutions
Example 1
Find the factors of 12.
Solution
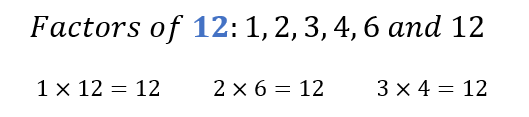
The numbers 1, 2, 3, 6, 4, and 12 divide 12 without leaving a remainder, making them factors of 12.
Example 2
Perform a prime factorization of 24.
Solution

Hence, 24 can be factored into 2×2×2×3, which are all prime numbers.
Example 3
Factorize: 9x2y+18xy3.
Solution
These are the factors of each term:
9x2y=3×3×x×x×y
18xy3=3×3×2×x×y×y×y
The common factors of the two terms are (3×3×x×y). Therefore,
9x2y+18xy3=(3×3×x×x×y)+(3×3×2×x×y×y×y) Prime Factorization
9x2y+18xy3=(3×3×x×y)[x+(2y)2]
9x2y+18xy3=(9xy)(x+2y2)
Example 4
Factorize: 36a2-25.
Solution
Notice that both terms are squares, but the second term is negative. The identity x2-y2=(x+y)(x-y) is applicable in this expression where x=6a and y=5. So we have,
36a2-25=(6a)2-52
36a2-25=(6a+5)(6a-5)
Therefore, the factors are (6a+5) and (6a-5).
Real-life Application with Solution
Problem 1
Suppose you have two wires with lengths of 24 feet and 32 feet, and you must cut these wires into pieces of equal length. What must be the maximum length of each piece?
Solution
Let us find the greatest common factor of 24 feet and 32 feet.
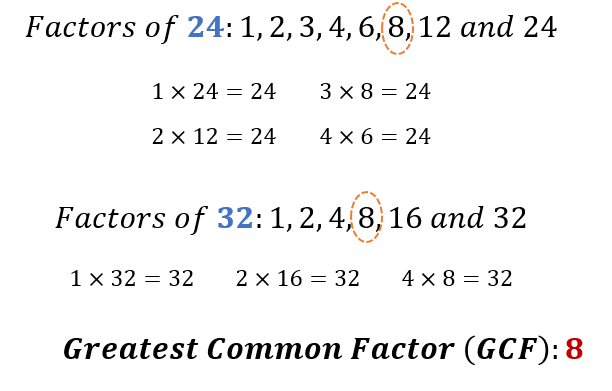
Therefore, the maximum length of each wire piece is 8 feet.
Problem 2
The product of two consecutive integers is 20. Find the value of each integer.
Solution
Let n be the first integer and n+1 be the second integer. Hence, (first integer)×(second integer)=20 or n(n+1)=20.
Multiplying the factors we have,
n(n+1)=20
n2+n=20 (Distributive Law)
n2+n-20=0 (Subtraction Property of Equality)
By using the factorization form x2+(a+b)x+ab=(x+a)(x+b), such that ab=-20 and a+b=1, we have,

The polynomial n2+n-20=(n+5)(n-4).
Calculating n, we have n+5=0 and n-4=0, giving us n=-5 and n=4.
Solving for the value of each integer, let us substitute the calculated values of n.
If n=-5, then n+1=-5+1=-4. Hence, the two integers are -4 and -5.
If n=4, then n+1=4+1=5. Hence, the two integers are 4 and 5.
Therefore, the integers are -4 and -5 or 4 and 5.
Practice Test
1. Perform a prime factorization of 50.
2. Perform a prime factorization of 72.
3. Factor the polynomial x2– 16.
4. Factor the polynomial x2-7x+10.
5. Find the factors of 3x2+9x+6
Answers:
1.

2.

3. Using the identity x2-y2=(x+y)(x-y), we have,
x2-16=(x)2-(4)2
x2-16=(x+4)(x-4)
4. Using the identity (x-y)2=x2-2xy+y2,
x2-7x+10=x2-5x-2x+10
x2-7x+10=(x2-5x)-(2x-10)
x2-7x+10=x(x-5)-2(x-5)
x2-7x+10=(x-2)(x-5)
5. Since 3 is a common factor of all the terms we have,
3×2+9x+6=3(x2+3x+2).
Factorizing (x2+3x+2) we follow x2+(a+b)x+ab=(x+a)(x+b)
x2+3x+2=x2+(2+1)x+(2)(1)
x2+3x+2=(x+2)(x+1)
Hence, 3x2+9x+6=3 (x+2)(x+1).
Frequently Asked Questions (FAQs)
Why is factorization important in mathematics?
Factorization is a fundamental concept in mathematics as it helps simplify complex numbers and expressions, solve equations, and understand number patterns.
What does it mean to factorize a polynomial?
Factorizing a polynomial means to write it as a product of two or more simpler polynomials.
What is a prime factor?
A prime factor is a factor of a number that is a prime number.
How do I find the GCF of two numbers?
To find the GCF of two numbers, you need to list the prime factors of each number and then multiply the common prime factors.
Can any number be factorized?
Yes. Any integer larger than one (1) can be factorized into prime numbers. However, we usually do not discuss factorization for negative numbers, zero, and one.
Recommended Worksheets
Factorization (Amelia Earhart Day Themed) Math Worksheets
Factors (Prime & Composite) Worksheet
GCF: Greatest Common Factor (Valentine’s Day Themed) Math Worksheets









