Home » Math Theory » Numbers » Co-prime Numbers

Co-prime Numbers

Before we dive into the actual definition of Co-prime Numbers, let’s have a recap first of what a Prime Number is. 

A prime number is a positive integer or number that has factors of 1 and the number itself. This means if a number has more than two factors, it is not prime but rather a composite number. And yes, we do not consider the negative integers because they have more than two factors. Let’s take a look at the illustration below to see the difference.

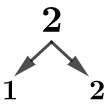
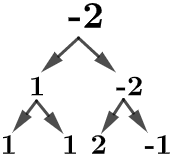
Now, let us list the factors of each number.

 2 = {1, 2}

-2 = {-2, -1, 1, 2}

By looking at the factor tree and the listed form of the factors above, we can easily conclude that positive 2 is a prime number because it has only two factors, which are 1 and itself. On the other hand, negative 2 is not a prime number, because it can also have -1 and 2 as factors. For this reason, we can expect that Co-prime numbers are pairs of positive numbers with unique properties, properties that we will see later.  

Using the definition of Prime Numbers, we notice that each number must have 1 as its “primary” factor. But now, we are going to talk about pairs of numbers that must have a “common primary” factor of 1. This gives us now the definition of Co-prime numbers.

Definition

Co-prime numbers (also known as Relatively Prime Numbers) are a pair of numbers that have the Greatest Common Factor (GCF) as 1. In other words, these are numbers that have no common or same factors other than 1. To check whether the pair are co-prime to each other, we can list their factors and find their Greatest Common Factor or GCF.

Notation in Number Theory

In Number Theory, co-prime numbers have the notation of GCD (a, b) = 1, or the Greatest Common Divisor of the pair of numbers (i.e. a and b) must be 1 to consider as co-prime numbers. For instance, let’s find the GCD of 37 and 13 with the Modular Arithmetic method to check if they are relatively prime or co-prime numbers.

GCD (37, 13); where a = 37, b = 13

GCD (a, b) = GCD (b, a mod b) 

GCD (37, 13) = GCD (13, 37 mod 13) 

                        = GCD (13, 11)

GCD (13, 11) = GCD (11, 13 mod 11) 

                        = GCD (11, 2)

GCD (11, 2) = GCD (2, 11 mod 2) 

                     = GCD (2, 1)

GCD (2, 1) = GCD (1, 2 mod 1) 

                   = GCD (1, 0)

Since GCD (37, 13) = GCD (1, 0), we can declare that GCD (37, 13) = 1. It means that 37 and 13’s Greatest Common Divisor is 1, and they are co-prime numbers.

“Divisors” VS “Factors”

But you may ask, “From the definition, the term ‘factor’ is used rather than ‘divisor’, are there any differences?” From what we did a while ago, we can divide 37 to any number (also known as the divisor), but the problem is, there would be a remainder. For instance, we divided 37 (dividend) by 13 (divisor), but we still have a remainder of 11. 

On the other hand, factors are divisors that can divide a number exactly or cannot result in any remainder. For that reason, the Greatest Common Factor (GCF) of the pair of numbers is commonly used to verify whether they are relatively prime to each other. Furthermore, you may notice that we can more quickly check if they are co-primes or not using only the factors rather than with divisors.

However, this does not mean that idea of GCD is not useful. As a matter of fact, this notation is widely used in real-life applications such as network security.

In a nutshell, for this topic, you can expect that there will be no negative numbers involved. Also, the term Greatest Common Factor will be used to verify if a pair of numbers are relatively prime or not.

Examples of Co-prime Numbers

Example 1 

7 and 11

For this situation, it is easier to visualize the factors by making a factor tree for each one of them so that we can list them later.

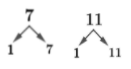
With these visualizations, we can now list their factors.

7 = {1, 7}

11 = {1, 11}

Looking at the list, we can notice that they have 1 as their Greatest Common Factor or GCF.

7 = {1, 7}

11 = {1, 11}

Therefore, 7 and 11 are relatively prime or co-prime numbers. Also, 7 and 11 are both prime numbers, how about a pair composite and prime numbers? Let’s see in the next example.

Example 2

6 and 13

Here, we have a composite (6) and a prime (13) number. Again, let’s create a factor tree to list their factors later.

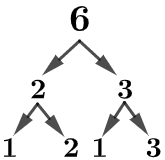
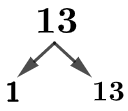
Now, we can list out the factors.

6 = {1, 2, 3, 6}

13 = {1, 13}

Here, we can notice that both of the numbers have the GCF of 1. 

6 = {1, 2, 3}

13 = {1, 13}

Hence 6, even though a composite number, is relatively prime to 13 which is a prime number. How about if we have a pair of composite numbers? Let’s try it in the next example.

Example 3

(15, 20)

For this case, let’s try it without using a factor tree, and just list the factors.

15 = {1, 3, 5, 15}

20 = {1, 2, 4, 5, 10, 20}

By looking at the list, we can see that they have 1 as a common factor, but they have 5 as well.

15 = {1, 3, 5, 15}

20 = {1, 2, 4, 5, 10, 20}

This means that 5 and 20’s Greatest Common Factor is 5 and not 1. Therefore, 15 and 20 are NOT co-prime numbers. However, this does not actually mean that all pairs of composite numbers are not co-prime. Let’s prove it in the next example.

Example 4

(8, 9)

8 = {1, 2, 4, 8}

9 = {1, 3, 9}

Here, we can see that even though they are both composite numbers, they have 1 as their GCF.

8 = {1, 2, 4, 8}

9 = {1, 3, 9}

Therefore, 8 and 9 are co-prime numbers.

Properties of Co-prime Numbers

From the examples we discussed, we realized the properties of co-prime numbers.

Property 1:

Any pair of prime numbers are relatively prime to each other. 

Since prime numbers only have 1 and themselves as the factors, it is automatic that their Greatest Common Factor (GCF) is 1.

Examples: (7, 11), (2, 5), and (3, 7)

Property 2: 

Numbers that are consecutive are considered as co-prime.

Since these numbers are just next to each other, their GCF would also be 1 by default.

Examples: (3, 4), (19, 20), and (99, 100)

Property 3: 

A pair of composite numbers can also be relatively prime, except even numbers (because they have a common factor of 2 which is greater than 1). Furthermore, with this idea, numbers that are multiples of the same number are not considered as co-prime.

Examples: (4, 15) 🗸 (both composite, but GCF is 1)

    (6, 12) ✕ (since they are even numbers)

    (15, 20) ✕ (since they are both multiples of 5)

Property 4:

The Least Common Multiple or LCM of co-prime numbers is their product.

Example 1: (4, 15)

      4 15 = 60

      To prove this, we can list out each of their multiples.

      4   = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, …}

    15 = {15, 30, 45, 60, 75, 90, 105, …} 

                    Therefore, (4, 15) are relatively prime or co-prime numbers.

Example 2: (6, 12)

                     6 × 12 = 72

                     Again, let us list their multiples.

                    6 = {6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72,…}

                                   12 = {12, 24, 36, 48, 60, 72, …}

Here, we can notice that they share the same multiples of 72. However, the least among them is 12. 

                                    6 = {6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72,…}

                                   12 = {12, 24, 36, 48, 60, 72, …} 

      Hence, (6, 12) are not co-prime numbers.

For this reason, if the numbers are not consecutive, getting the product of the pair of numbers and checking if it is their LCM would also be a good trick to verify quickly whether they are co-prime numbers. 

Co-prime Numbers from 1-100

For you to be familiar with Co-prime Numbers, let us explore the pairs of them from 1-100. There are several co-prime numbers within this range, including the pairs that are consecutive or next to each other. Here are some of them.

1, 22, 33, 44, 55, 66, 77, 88, 99, 1010, 11
1, 32, 53, 54, 75, 76, 87, 98, 109, 1110, 13
1, 42, 73, 64, 95, 86, 97, 108, 119, 1210, 15
1, 52, 93, 74, 115, 96, 107, 118, 129, 1310, 17
1, 62, 113, 84, 135, 116, 117, 128, 139, 1410, 19
1, 72, 133, 104, 155, 126, 127, 138, 149, 1510, 21
1, 82, 153, 114, 175, 136, 137, 158, 159, 1610, 23
1, 92, 173, 134, 195, 146, 147, 168, 169, 1710, 25
1, 102, 193, 144, 215, 166, 157, 178, 179, 1910, 27
1, 112, 213, 154, 235, 176, 167, 188, 189, 2010, 29
11, 1212, 1313, 1414, 1515, 1616, 1717, 1818, 1919, 2020, 21
11, 4012, 3913, 2014, 2315, 6316, 2117, 5318, 3519, 3220, 33
11, 5812, 5313, 2814, 2915, 3116, 4517, 6418, 4719, 5020, 41
11, 7612, 6713, 3614, 3515, 3916, 6917, 7518, 5919, 8920, 49
11, 9412, 8113, 4414, 4115, 4716, 9317, 8618, 7119, 9620, 57
21, 2222, 2323, 2424,2525, 2626, 2727, 2828, 2929, 3030, 31
21, 4022, 5123, 5624, 3925, 5426, 5727, 4328, 6729, 3230, 37
21, 5222, 6723, 6224, 5525, 6626, 7127, 6528, 7529, 3530, 49
21, 6422, 8323, 6824, 7125, 7826, 8527, 7628, 8329, 5230, 67
21, 7623, 4423, 7424, 8725, 9026, 9927, 9829, 4929, 6930, 85
21, 8823, 5023, 8025, 4226, 4327, 3228, 5929, 8829, 8630, 91
31, 3232, 3333, 3434, 3535, 3636, 3737, 3838, 3939, 4040, 41
31, 4032, 4733, 5334, 4135, 5236, 4937, 6038, 4139, 5040, 57
31, 4832, 6133, 6834, 4735, 6836, 6137, 7338, 4339, 6040, 63
31, 5632, 7733, 8534, 5335, 8436, 7337, 8238, 4539, 7040, 81
31, 6432, 8933, 9234, 5935, 9936, 8537, 9038, 4739, 8040, 93
50, 5151, 5252, 5353, 5454, 5555, 5656, 5757, 5858, 5959, 60
60, 7361, 5062, 7763, 8064, 7365, 8966, 6767, 8268, 9569, 70
70, 8971, 8272, 9973,  8574, 8775, 8176, 8377, 7878, 8579, 80
80, 8381, 9082, 9583, 9784, 9585, 9886, 9387, 9788, 9189, 99
90, 9191, 9292, 9393, 9494, 9595, 9696, 9797, 9898, 9999, 100

Co-prime Numbers Activity

Now, let’s have some exercises for you to identify whether the pair in the first column is co-prime or not.

Directions: List in the second column the factors of each pair of the numbers from the first column. Then, write the Greatest Common Factor or GCF of each pair in the third column. In the fourth column, write Yes if the pair is co-prime and No if it is not. Lastly, write the reason (referencing the Properties of Co-prime Numbers) for your answers from the fourth column to the fifth column. The first row serves as an example.                           

PairFactorsGreatest Common FactorCo-prime?Why?

(19, 20)
19 = {1, 19}20 = {1, 2, 4, 5, 10, 20}
1
Yes
They are consecutive numbers.

(6, 24)

(7, 27)

(3, 33)

(10, 81)

(49, 63)

(56, 57)

(4, 9)

(88, 99)

(2, 21)

(5, 17)

Solution for the Activity:

PairFactorsGreatest Common FactorCo-prime?Why?

(19,20)
19 = {1, 19}20 = {1, 2, 4, 5, 10, 20}
1
Yes
They are consecutive numbers.

(6, 24)
6 = {1, 2, 3, 6}24 = {1, 2, 4, 6, 12, 24}
6
No
They are both even numbers.

(7, 27)
7 = {1, 7}27 = {1, 3, 9, 27}
1
Yes
Their GCF is 1.

(3, 33)
3 = {1, 3}33 = {1, 3, 11, 33}
3
No
Both are multiples of 3, which makes 3 also as their GCF.

(10, 81)
10 = {1, 2, 5, 10}81 = {1, 3, 9, 27, 81}
1
Yes
They are both composite, but not even numbers and multiples of the same number.

(49, 63)
49 = {1, 7, 49}63 = {1, 3, 7, 9, 21, 63}
7
No
Both are multiples of 7, which makes 7 also as their GCF.

(56, 57)
56 = {1, 2, 4, 7, 8, 14, 28, 56}57 = {1, 3, 19, 57}
1
Yes
They are consecutive numbers.

(4, 9)
4 = {1, 2, 4}9 = {1, 3, 9}
1
Yes
They are both composite, but not even numbers and multiples of the same number.

(88, 99)
88 = {1, 2, 4, 8, 11, 22, 44, 88}63 = {1, 3, 9, 11, 33, 99}
11
No
Both are multiples of 11, which makes 11 also as their GCF.

(2, 21)
2 = {1, 2}21 = {1, 3, 7, 21}
1
Yes		Their product is 42 which is also their Least Common Multiple.

(5, 17)		5 = {1, 5}17 = {1, 17}
1
Yes
They are both prime numbers.

Where are Co-prime numbers used for?

So, we mastered the knowledge of co-prime numbers. But, what are their purposes? In reality, there are many uses of relatively prime numbers, but here are common applications. 

  1. Cryptography and Cybersecurity

Imagine that you forgot your password in your online bank account, and you hit the “Forgot Password” button to demand a code. After a few seconds, the bank sent you a code to your email address or phone number, a code that only you and the bank know. Of course, you do not want anyone to hack your account so you changed again your password and made sure that it is well-secured. But how will the bank have access to your account with security measures? Also, keep in mind that each character of your password is actually represented by numbers to encrypt it for the sake of security. Well, this is when decryption of your password enters and one of those steps is finding the co-prime of a number that represents one of the characters of your passwords. With that process, the bank can now have access to your account without any security breach and also, hackers.

  1. Mechanical Engineering

The concept of relatively prime numbers is well used by engineers especially in contacting gears. Keep in mind that gears must function without any damage. And to do that, the number of teeth of the two gears should be relatively prime so that they will not be rubbing in each other which can result in dismantling. For instance, a pair of gears with teeth of 30 and 35 is considered poor, because the second gear may hit some teeth of the first gear. While having co-prime numbers of teeth such as 31 and 35 is considered excellent.

Key Facts & Summary

  • Co-prime or relatively prime numbers are a pair of numbers that has only 1 as the Greatest Common Factor or GCF.
  • In number theory, co-prime numbers are notated as GCD (a, b) = 1. 
  • The term divisors is pertaining to all numbers that can divide a number but can have a remainder. On the other hand, factors are referring to the divisors that can divide a number exactly.
  • Relatively prime or co-prime numbers have unique properties:
    • All pairs of prime numbers are relatively prime.
    • Consecutive numbers are co-prime by default.
    • Pair of even numbers and numbers that are multiples of the same number are not co-prime.
    • The product of co-prime numbers must also be their Least Common Multiple or LCM.
  • There is infinite list of co-prime numbers within the range of 1-100.
  • There are many ways co-prime numbers can be applied to our daily lives.

Prime Numbers (Diwali Themed) Math Worksheets
Prime and Composite Numbers (Halloween Themed) Worksheets
LCM: Least Common Multiple (Earth Day Themed) Math Worksheets

Browse All Worksheets

Link/Reference Us

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!

  • "Co-prime Numbers". Helping with Math. Accessed on April 19, 2024. https://helpingwithmath.com/co-prime-numbers/.

  • "Co-prime Numbers". Helping with Math, https://helpingwithmath.com/co-prime-numbers/. Accessed 19 April, 2024.

  • Co-prime Numbers. Helping with Math. Retrieved from https://helpingwithmath.com/co-prime-numbers/.