Introduction
Clocks are more than just instruments that tell us time. They can also be a fascinating subject for learning some cool math. In this article, we will talk about the “Clock Angle Formula,” a fun way to use math to calculate the angle between the hour and minute hand on a clock. Yes, you read it right! You can use math with a simple clock, and it is pretty exciting.
Grade Appropriateness
The Clock Angle Formula is generally suitable for middle and high school students, specifically grades 6 to 9. Students in this age range, typically 11 to 15, are beginning to explore geometry and angles, making this a perfect topic.
Math Domain
The domain of this mathematical concept is Geometry. This topic explicitly addresses concepts like angles, degrees, and how circular motion is represented mathematically. It involves the use of basic arithmetic and a little bit of algebra.
Applicable Common Core Standards
The clock angle problem aligns with the following Common Core Standards:
CCSS.Math.Content.4.MD.C.5: Recognize angles as geometric shapes that are formed wherever two rays share a typical endpoint, and understand concepts of angle measurement:
CCSS.Math.Content.7.G.B.5: Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure.
Definition of the Topic
Finding the angle between a clock’s hour and minute hands at a given time is known as the “clock angle problem.” The problem is generally solved using a formula referred to as the “Clock Angle Formula.”

Key Concepts
To understand the Clock Angle Formula, we first need to understand some key concepts:
Hour Hand and Minute Hand: The hour hand is the shorter hand on the clock that shows the hour. The minute hand is the longer hand that shows the minutes past the hour.
Angle: The distance between two intersecting lines or near their point of intersection is known as an angle and is often measured in degrees.
Degree: A unit of measurement of angles, 1/360 of the circumference of a circle.
Discussion with Illustrative Examples
A clock determines the time of day. There are three hands: a second hand, a minute hand, and an hour hand.
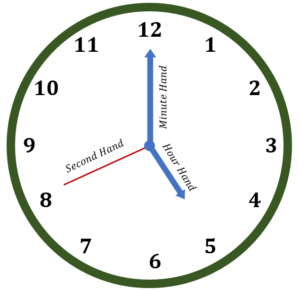
Hour and Minute Hand Derivation
A clock has 12 sectors; just like a circle, it has 360°.
The angle between two numbers or divisions is 30°.
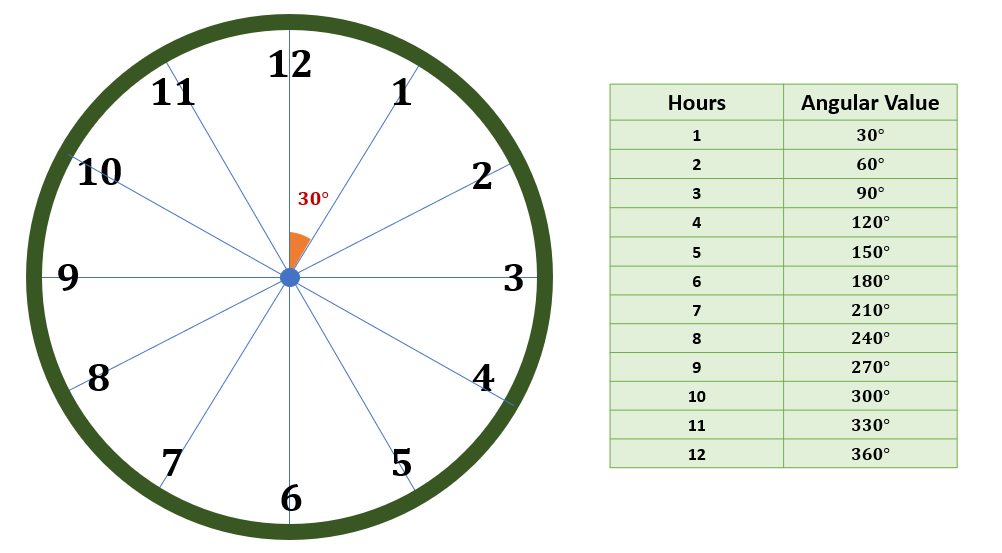
12 hours=360°
1 hour=$\frac{360°}{12}$
1 hour=30°
The hour hand moves 30° in one hour; therefore, each minute, the hour hand moves by half a degree, that is, $\frac{30°}{60}$=0.5°
Between two divisions has a 5-minute interval or parts, and 1 minute is equivalent to 6°.

60 minutes=360°
1 minute=$\frac{360°}{60}$
1 minute=6°
Clock Angle Formula
The clock angle formula is used to solve the time or angle between a clock’s hour hand and minute hand.
Minute hand’s angle with respect to the line at 12 o’clock:
Angleminutes=6°×Number of minutes
Hour hand’s angle with respect to the line at 12 o’clock:
Anglehours=(30°×Number of hours)+(0.5×Number of minutes)
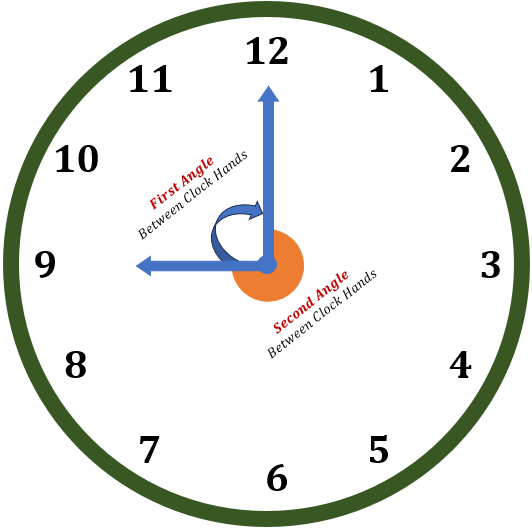
The first angle between the clock hands
|Anglehours-Angleminutes|
The second angle between the clock hands
360°-First angle
The vertical bars “|” denote absolute value, meaning the result is always positive.
Two Clock Angles
The clockwise angle from the hour hand to the minute hand is the first angle between the clock hands. The second angle between clock hands is the counterclockwise angle from the hour hand to the minute hand.
Examples with Solutions
Example 1
Find the angle between the hour and minute hands at 9:00 PM.
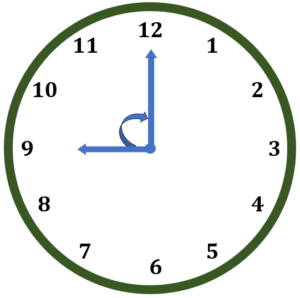
Solution
Substituting the number of hours, 9, we have,
Anglehours=30°×9
Anglehours=270°
270° is the angle from the line at 12 o’clock to the minute hand.
Since a circle has 360°, we subtract 270° from 360°.
360°-270°=90°
Therefore, the angle between the hour and minute hands at 9:00 PM is 90°.
Example 2
If a clock shows at 3:10 AM, what is the measure of the two clock angles?
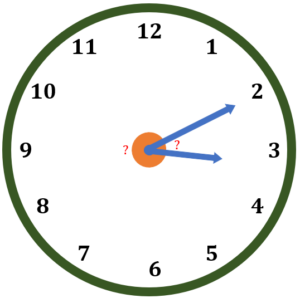
Solution
Solve the angle between the minute hand and the line at 12 o’clock.
Angleminutes=6°×Number of minutes
Angleminutes=6°×10
Angleminutes=60°
The hour hand moves every minute. Calculate the angle for the hour considering the number of minutes.
Anglehours=(30°×Number of hours)+(0.5°×Number of minutes)
Anglehours=(30°×3)+(0.5°×10)
Anglehours=90°+5°
Anglehours=95°
To find the two angles, we have,
| The first angle between the clock hands |Anglehours-Angleminutes| |95°-60°| 35° | The second angle between the clock hands 360°-First Angle 360°-35° 325° |
Therefore, the two angles if the clock shows 3:10 AM are 35° and 325°.
Real-life Application with Solution
Suppose you are making a poster for a school event scheduled to start at 8:15. You want to draw a clock on the poster showing the event’s start time. You want the clock to be accurate, so you need to find the angle between the hour and minute hand at 8:15.
Solution
Using the formula where 8 is the number of hours, and 15 is the number of minutes, we have,
Angleminutes=6°×Number of minutes
Angleminutes=6°×15
Angleminutes=90°
Anglehours=(30°×Number of hours)+(0.5°×Number of minutes)
Anglehours=(30°×8)+(0.5°×15)
Anglehours=240°+7.5°
Anglehours=247.5°
The angle between the clock hands
|Anglehours-Angleminutes|
|247.5°-90°|
157.50°
You must draw the hands 157.5 degrees apart on your poster!
Practice Test
Let’s see if you can figure out these angles on your own:
1. What is the clock angle between the hands at 4:00?
2. What is the clock angle between the hands at 10:00?
3. What is the clock angle between the hands at 7:20?
4. What is the clock angle between the hands at 9:15?
5. Find the measure of the two clock angles at 1:25?
Answers:
1. Clock angle between the hands at 4:00
Anglehours=(30°×Number of hours)+(0.5°×Number of minutes)
Anglehours=(30°×4)+(0.5°×0)
Anglehours=120°+0°
Anglehours=120°
2. Clock angle between the hands at 10:00
Anglehours=(30°×Number of hours)+(0.5°×Number of minutes)
Anglehours=(30°×10)+(0.5°×0)
Anglehours=300°+0°
Anglehours=300°
3. Clock angle between the hands at 7:20
Angleminutes=6°×Number of minutes
Angleminutes=6°×20
Angleminutes=120°
Anglehours=(30°×Number of hours)+(0.5°×Number of minutes)
Anglehours=(30°×7)+(0.5°×20)
Anglehours=210°+10°
Anglehours=220°
The angle between the clock hands
|Anglehours-Angleminutes|
|220°-120°|
100°
4. Clock angle between the hands at 9:15
Angleminutes=6°×Number of minutes
Angleminutes=6°×15
Angleminutes=90°
Anglehours=(30°×Number of hours)+(0.5°×Number of minutes)
Anglehours=(30°×9)+(0.5°×15)
Anglehours=270°+7.5°
Anglehours=277.5°
The angle between the clock hands
|Anglehours-Angleminutes|
|277.5°-90°|
187.5°
5. Two clock angles at 1:25
Angleminutes=6°×Number of minutes
Angleminutes=6°×25
Angleminutes=150°
Anglehours=(30°×Number of hours)+(0.5°×Number of minutes)
Anglehours=(30°×1)+(0.5°×25)
Anglehours=30°+12.5°
Anglehours=42.5°
The first angle between the clock hands
|Anglehours-Angleminutes|
|42.5°-150°|
|-107.5|
107.5°
The second angle between the clock hands
360°-First Angle
360°-107.5°
252.5°
Frequently Asked Questions (FAQs)
Is the clock angle always calculated in degrees?
Yes, the clock angle is typically calculated in degrees as it is a common unit of measurement for angles.
What if the clock angle formula gives a value of more than 180 degrees?
The formula always gives a smaller angle between the clock hands. If you get a value of more than 180 degrees, subtract it from 360 to find the smaller angle.
Can the clock hands form a straight line?
Yes, the clock hands form a straight line twice during a 12-hour cycle, once at 12:00 and then again at 6:00.
Can this formula be used on digital clocks?
No. The clock angle formula applies only to analog clocks with hour and minute hands.
How often do the hour and minute hand overlap?
The hour and minute hand overlap 22 times daily (24 hours).
Learning the Clock Angle Formula is a fun and engaging way to understand the principles of geometry and angles. The next time you look at a clock, you can impress your friends by quickly figuring out the angle between the hands!
Recommended Worksheets
Clock Angle Formula (Budgeting Themed) Math Worksheets
3-Figure Bearings (International Seafarer Day Themed) Math Worksheets
Central Angle of a Circle (Fast Food Themed) Math Worksheets









