DEFINITION OF MEASUREMENT
Measurement means to describe and compare mathematical and concrete objects using numbers and measurement units. To measure something is to determine how large or small a physical quantity is compared to its reference unit. In mathematics, measurement focuses on properties such as length, mass and weight, time, money, and temperature. Moreover, it is also involved in finding the perimeter, area, surface area, volume, and angle measure.
WHAT IS MEASUREMENT UNITS?
Measurement units is a standardized quantity used to represent physical quantity. When we say it is a unit of, it simply means there is one of. 1 meter, 1 second, 1 kilogram, etc. are all units.
SYSTEMS OF MEASUREMENT UNITS
The system of units differs from country to country. These systems are composed of set of rules and units of measurements relating them to each other.
TRADITIONAL SYSTEM
During the ancient times, measurement is usually based on human body and nature. For example, using the thumb, the span of hands and arms, and the foot to measure lengths. More so, ancients based the time by the cast of shadow of the vertical stick and by the movement of sun. The methods used by the ancients were later developed to make a standardized and universal system.
INTERNATIONAL SYSTEM OF UNITS
The International System of Units, also known as SI Units, is the current globally used metric system. The system was established in 1960 at the General Conference on Weights and Measures.
BASE UNITS
The table below shows the seven base units of the SI Units.
| Unit Name | Unit Symbol | |
| Length | meter | m |
| Weight | kilogram | kg |
| Time | second | s |
| Current | ampere | A |
| Thermodynamic temperature | kelvin | K |
| Amount of substance | mole | mol |
| Luminosity | candela | cd |
DERIVED UNITS
Derived units are units which can be expressed in terms of base units by means of multiplication and division symbols. The table shows some of the derived SI units.
| Name | Symbol | |
| Area | square meter | $m^{2}$ |
| Volume | cubic meter | $m^{3}$ |
| Speed, Velocity | meter per second | $m/s$ |
| Acceleration | meter per second squared | $m/s ^{2}$ |
| Density, Mass Density | kilogram per cubic meter | $kg/m^{3}$ |
| Specific Volume | cubic meter per kilogram | $m^{3}/kg$ |
NON-SI UNITS
Non-SI units are units that is accepted for use with SI. Most of these non-SI units are continuously used every day.
| Name | Symbol | Value in SI Units |
| minute | min | 60 s |
| hour | h | 1 h = 60 min = 3 600 s |
| day | d | 1 d = 24 h = 86 400 s |
| degree of arc | ° | $1^{\circ}=(\frac{\pi }{180})rad$ |
| minute of arc | ‘ | $1’=(\frac{1}{60})^{\circ}=(\frac{\pi }{10800})rad$ |
| second of arc | ” | $1”(\frac{1}{60})’=(\frac{\pi }{648000})rad$ |
| liter | l, L | $1 l=1dm^{3}=10^{-3} m^{3}$ |
| ton | t | $1 t=10^{3}kg$ |
SI PREFIXES
SI prefixes are used to identify multiples or fractions of the base units. The table below shows the SI prefixes, symbol, and multiplicative factor.
| Prefix | Symbol | Multiplication Factor/ Scientific Notation |
| Yotta | Y | $10^{24}$ |
| Zetta | Z | $10^{21}$ |
| Exa | E | $10^{18}$ |
| Peta | P | $10^{15}$ |
| Tera | T | $10^{12}$ |
| Giga | G | $10^{9}$ |
| Mega | M | $10^{6}$ |
| Kilo | k | $10^{3}$ |
| Hecto | h | $10^{2}$ |
| Deca | da | $10^{1}$ |
| $10^{0}$ | ||
| Deci | d | $10^{-1}$ |
| Centi | c | $10^{-2}$ |
| Milli | m | $10^{-3}$ |
| Micro | $\mu$ | $10^{-6}$ |
| Nano | n | $10^{-9}$ |
| Pico | p | $10^{-12}$ |
| Femto | f | $10^{-15}$ |
| Atto | a | $10^{-18}$ |
| Zepto | z | $10^{-21}$ |
| Yocto | y | $10^{-24}$ |
BRITISH IMPERIAL SYSTEM
British Imperial System, also called as Imperial Units, is the official weights and measures system used in Great Britain from 1824 to 1965.
IMPERIAL UNITS FOR LENGTHS
| Unit | Symbol | Equivalent to Feet |
| twip | 1/17280 | |
| thou | th | 1/12000 |
| barleycorn | Bc | 1/36 |
| inch | in, ” | 1/12 |
| hand | h | 1/3 |
| foot | ft, ‘ | |
| yard | yd | 3 |
| fathom | fth | 6 |
| rod | rd | 16.5 |
| chain | ch | 66 |
| furlong | fur | 660 |
| mile | mi | 5 280 |
| nautical mile | nmi | 6 076 |
| league | lea | 15 840 |
IMPERIAL UNITS FOR AREA
| Unit | Equivalent to Feet |
| perch | 272 1/4 |
| rood | 10 890 |
| acre | 43 560 |
| square mile | 27 878 400 |
IMPERIAL UNITS FOR LIQUID AND DRY MEASURES
| Unit | Unit Symbol | Capacity |
| gill | gi | $8.64in^{3}$ |
| pint | pi | $34.76in^{3}$ |
| quart | qt | $69.32in^{3}$ |
| gallon | gal | $277.274in^{3}$ |
| bushel | bu | $1.109.096 in^{3}$ |
US CUSTOMARY SYSTEM
The US Customary System Unit is a system of measurement used in the United States and its territories since 1832. Americans use this system in commercial, personal, and social use.
US CUSTOMARY SYSTEM UNITS FOR LENGTHS
| Unit | Unit Symbol | Equivalent to Feet |
| point | p | 1/864 |
| pica | P | 1/72 |
| inch | in, ” | 1/12 |
| foot | ft, ‘ | 1 |
| yard | yd | 3 |
| mile | mi | 5280 |
US CUSTOMARY SYSTEM FOR DRY VOLUME
| Unit | Unit Symbol | SI Equivalent |
| pint | pt | 0.5506104713575 L |
| quart | qt | 1.101221 L |
| gallon | gal | 4.404884 L |
| peck | pk | 8.809768 L |
| bushel | bu | 35.23907016688 L |
| barrel | bbl | 115.6271 L |
US CUSTOMARY SYSTEM FOR LIQUID VOLUME
| Unit | Unit Symbol | SI Equivalent |
| minim | min | 61.611519921875 μL |
| fluid dram | fl dr | 3.6966911953125 mL |
| teaspoon | tsp | 4.92892159375 mL |
| tablespoon | tbsp | 14.78676478125 mL |
| fluid ounce | fl oz | 29.5735295625 mL |
| shot | jig | 44.36029434375 mL |
| gill | gi | 118.29411825 mL |
| cup | c | 236.5882365 mL |
| pint | pt | 473.176473 mL |
| quart | qt | 0.946352946 L |
| pottle | pot | 1.892705892 L |
| gallon | gal | 3.785411784 L |
| barrel | bbl | 119.240471196 L |
| oil barrel | bbl | 158.987294928 L |
| hogshead | 238.480942392 L |
LENGTH
DEFINITION OF LENGTH
Length is an attribute that describes how long a thing is from one end to the other. It is used to identify how long or short think or thick the size of an object or part of an object is. The unit system of length also determines the thickness and thinness of an object.
METRIC SYSTEM VS US CUSTOMARY SYSTEM
| SI UNIT (METRIC SYSTEM) | US CUSTOMARY SYSTEM |
| Millimeter (mm): it is used to measure very short lengths and thicknesses. EXAMPLE: thickness of a coin, length of a pencil tip | Inch (in): it is used to measure the length of small objects. EXAMPLE: length of a table, thickness of a book |
| Centimeter (cm): it is used to measure small lengths of an object EXAMPLE: length of a pen | Foot (ft): it is used to measure short distances and heights. EXAMPLE: height of a person, height of a building |
| Meter (m): it is used to measure longer lengths of an object EXAMPLE: length of a room | Yard (yd): usually used to measure longer lengths and fields EXAMPLE: length of a backyard, length of a football field |
| Kilometer (km): it is used to measure distance and very long lengths | Mile (mi): it is usually used to measure distance between two places |
CONVERSION OF LENGTHS
CONVERTING LENGTHS IN SI UNITS
To convert length measures given different SI Units, you must:
- Take note of the SI prefixes and its multiplicative factors.
- Multiply the given by the multiplicative factor to which you will convert it.
- Always put the label of measurement.
The table below shows the different measures in lengths and its multiplicative factor.
| Multiplication Factor/ Scientific Notation | |
| kilometer | $10^{3}$ |
| hecto | $10^{2}$ |
| deca | $10^{1}$ |
| meter | $10^{0}$ |
| deci | $10^{-1}$ |
| centi | $10^{-2}$ |
| milli | $10^{-3}$ |
EXAMPLE #1
Convert 2,867 kilometers to meters.
SOLUTION
Since kilometer is greater than meters, we will multiply the given to its multiplicative factor. Based on the SI prefixes, the multiplicative factor between kilometer and meter is . Thus, we will multiply 2,867 by or 1000.
$2 867 km \times \frac{1000m}{1km}=2 867 000 m$
Therefore, 2,867 km when converted to meters is 2 867 000 m.
EXAMPLE #2
Convert 821 centimeters to meters.
SOLUTION
To convert centimeters to meters, we will simply divide its multiplicative factor to the given since centimeters is smaller than meters. The multiplicative factor between centimeter and meter is $10^{-2}$ or $\frac{1}{100}$. Hence,
$821cm\times \frac{1m}{100cm}=8.21 m$
Therefore, 821 cm is also equal to 8.21 m.
CONVERTING LENGTHS IN US CUSTOMARY SYSTEM
To convert lengths using the US Customary System, you must:
- Remember the equivalent measures of certain units.
- Multiply the given to the conversion factor to which you are going to convert it.
- Always put the label of measurement.
EXAMPLE #1
How many feet are there in 27 yards?
SOLUTION
To convert yards to feet, simply multiply 27 yards to 3 feet since yards is larger than feet. Hence,
$27 yd \times \frac{3ft}{1yd}=81ft$
Therefore, 27 yards when converted to feet is 81 ft.
EXAMPLE #2
How many feet are there in 30 inches?
SOLUTION
To convert inches to feet, simply multiply 30 inches to 1/12 feet. Thus,
$30 in\times \frac{1ft}{12in}=2.5ft$
Thus, 30 inches is equal to 2.5 feet.
CONVERTING LENGTHS TO US CUSTOMARY SYSTEM AND SI UNIT
The table below shows the equivalent measures of US Customary System to the current Metric System, SI Unit. This table will be helpful in converting lengths from US Customary measures to SI Unit measures, and vice versa.
| US Customary | SI Unit Equivalent |
| 1 point | 0.3528 mm |
| 1 pica | 4.2333 mm |
| 1 inch | 25.4 mm |
| 1 foot | 30.48 cm |
| 1 yard | 0.91 m |
| 1 mile | 1.61 km |
EXAMPLE #1
Convert 9.3 miles to kilometers.
SOLUTION
To convert 9.3 miles to kilometers, simply multiply 9.3 miles to 1.61km.
$9.3 mi \times \frac{1.61km}{1mi}=14.973$
Therefore, 9.3 miles is equal to 14.973 km.
EXAMPLE #2
What is 400 meters when converted to pica?
SOLUTION
Given the equivalent table for US Customary and SI units, we only have 1 pica = 4.2333 mm. So, we will first convert 4 meters to millimeters.
$4 m \times \frac{1000mm}{1m}=4 000 mm$
Next step is to convert 4000 mm to pica. Since 1 pica = 4.2333 mm, we will put 4.2333 mm to the denominator.
$4 000 mm \times \frac{1pica}{4.2333 mm}=944.889 pica$
Therefore, 4 meters is equal to 944.889 pica.
MASS AND WEIGHT
DEFINITION OF WEIGHT
Weight is an attribute that measures how heavy an object is.
METRIC SYSTEM VS US CUSTOMARY SYSTEM
| SI UNIT (METRIC SYSTEM) | US CUSTOMARY SYSTEM |
| Milligram (mg): it is used to measure weight of light objects. EXAMPLE: medicine, ink of a pen | Ounce (oz): it is usually used to measure small quantities. EXAMPLE: cola |
| Gram (g): it is used to measure weight of small objects or weight of small quantity ingredients. EXAMPLE: weight of a paperclip | Pound (lb): it is usually used to measure body weight |
| Kilogram (kg): it is used to measure heavy objects EXAMPLE: body weight | Ton: it is used to measure heavy objects EXAMPLE: weight capacity of truck |
CONVERSION OF WEIGHT
CONVERTING WEIGHTS IN SI UNITS
To convert weight measures given different SI Units, you must:
- Take note of the SI prefixes and its multiplicative factors.
- Multiply the given by the multiplicative factor to which you will convert it.
- Always put the label of measurement.
The table below shows the different measures in lengths and its multiplicative factor.
| Multiplication Factor/ Scientific Notation | |
| Kilogram | $10^{3}$ |
| Hectogram | $10^{2}$ |
| Decagram | $10^{1}$ |
| Gram | $10^{0}$ |
| Decigram | $10^{-1}$ |
| Centigram | $10^{-2}$ |
| milligram | $10^{-3}$ |
EXAMPLE
Convert 7 kilograms to milligram.
SOLUTION
To convert 7 kilograms to milligram, we need to convert it first to gram. Thus,
$7kg \times \frac{1000g}{1kg}=7000 g$
Then, convert 7000 grams to milligrams by:
$7000 g \times \frac{1000mg}{1g}=7 000 000 mg$
Therefore, 7 kilograms is the same as 7 000 000 mg
CONVERTING WEIGHTS IN US CUSTOMARY SYSTEM
To convert weights using the US Customary System, you must:
- Remember the equivalent measures of certain units.
- Multiply the given to the conversion factor to which you are going to convert it.
- Always put the label of measurement.
| US Customary | US Customary Equivalent |
| 1 pound | 16 ounces |
| 1 ton | 2000 pounds |
EXAMPLE
What is the equivalent measure of 124 ounces to pounds?
SOLUTION
Since pounds is a greater measure than ounces, we will put the equivalent measure in the denominator of the multiplicative factor. Thus,
$4oz\times \frac{1lb}{16oz}=7.75 lb$
Therefore, 124 oz is equal to 7.75 lb.
CONVERTING WEIGHTS TO US CUSTOMARY SYSTEM AND SI UNIT
The table below shows the equivalent measures of US Customary System to the current Metric System, SI Unit. This table will be helpful in converting weights from US Customary measures to SI Unit measures, and vice versa.
| US Customary | SI Unit Equivalent |
| 1 ounce | 28.35 g |
| 1 pound | 0.453 kg |
| 1 ton | 907.18 kg |
EXAMPLE
Kyle weighs 50 kg, what is his weight if converted into pounds?
SOLUTION
To convert Kyle’s weight into pounds, multiply 50 kg by $\frac{1lb}{0.453kg}$. Thus,
$50kg\times \frac{1lb}{0.453kg}=110.38 lb$
CAPACITY
DEFINITION OF CAPACITY
Capacity is the maximum amount of a what a container can hold.
CONVERTING CAPACITY
CONVERTING CAPACITY IN SI UNITS
To convert capacity measures given different SI Units, you must:
- Take note of the SI prefixes and its multiplicative factors.
- Multiply the given by the multiplicative factor to which you will convert it.
- Always put the label of measurement.
The table below shows the different measures in lengths and its multiplicative factor.
| Multiplication Factor/ Scientific Notation | |
| kiloliter | $10^{3}$ |
| hectoliter | $10^{2}$ |
| decaliter | $10^{1}$ |
| liter | $10^{0}$ |
| deciliter | $10^{-1}$ |
| centiliter | $10^{-2}$ |
| milliliter | $10^{-3}$ |
EXAMPLE
Convert 8.3 liters to milliliters.
SOLUTION
To convert 8.3 liters to milliliters, multiply $\frac{1000mL}{1L}$ to 8.3 liters.
$8.3 L\times \frac{1000mL}{1L}=8300 mL$
Thus, 8.3 L is equivalent to 8300 mL.
CONVERTING WEIGHTS IN US CUSTOMARY SYSTEM
To convert weights using the US Customary System, you must:
- Remember the equivalent measures of certain units.
- Multiply the given to the conversion factor to which you are going to convert it.
- Always put the label of measurement.
| US Customary | US Customary Equivalent |
| 1 ounce | 2 tablespoons |
| 1 cup | 8 ounces |
| 1 pint | 2 cups |
| 1 quart | 2 pints |
| 1 gallon | 4 quarts |
EXAMPLE
How many ounces are there in 4 pints?
SOLUTION
To find out how many ounces are there in 4 pints, convert 4 pints to cups first. Hence,
$4 pt\times \frac{2c}{1pt}=8c$
Then, convert 8 cups to ounces. Thus,
$8c\times \frac{8oz}{1c}=64 oz$
Therefore, there are 64 oz in 4 pints.
CONVERTING WEIGHTS TO US CUSTOMARY SYSTEM AND SI UNIT
The table below shows the equivalent measures of US Customary System to the current Metric System. This table will be helpful in converting capacity from US Customary measures to SI Unit measures, and vice versa.
| US Customary | SI Equivalent |
| 1 ounce | 29.574 mL |
| 1 cup | 236.588 mL |
| 1 pint | 473.176 mL |
| 1 quart | 0.946 L |
| 1 gallon | 3.785 L |
EXAMPLE #1
What is 3 gallons when converted to liters?
SOLUTION
To convert 3 gallons to liters, simply multiply 3.785 liters to 3 gallons. Thus,
$3 gal\times \frac{3.785 L}{1 gal}=11.355 L$
Therefore, there are 11.355 L or 11.36 L in 3 gallons.
EXAMPLE #2
Convert 7.5 liters to quarts.
SOLUTION
To convert 7.5 liters to quarts, multiply $\frac{1qt}{0.946 L}$ to 7.5 liters. Thus,
$7.5 L\times \frac{1qt}{0.946 L}=7.928 qt$
Therefore, there are 7.928 quarts or 7.93 quarts in 7.5 liters.
TIME
DEFINITION OF TIME
Time is the continuous sequence of events from past, present, and to the future. It is used to measure certain periods during an action, process, or event. We can measure time based on seconds, minutes, hours, days, weeks, and years by using clocks and calendars.

Time – Definition with Examples, digital photograph, SplashLearn, https://www.splashlearn.com/math-vocabulary/time/time. Accessed 23 Sept. 2021.
CONVERSION OF TIME
The table below shows the standard units of time and its equivalent measures.
| Equivalent measure | |
| 1 minute | 60 seconds |
| 1 hour | 60 minutes |
| 1 day | 24 hours |
| 1 week | 7 days |
| 1 year | 12 months |
| 1 year | 365 days |
| 1 year | 52 weeks |
In converting time in terms of months to days, the number of days will depend on the corresponding month as it sometimes can be 27 days, 28 days, 30 days, or 31 days. Meanwhile, during leap years, the number of days in a year is 366 days.
EXAMPLE
How many hours are there in 5 days?
SOLUTION
To convert hours to days, simply multiply 24 hours to the number of days. Hence,
$5 d\times \frac{24h}{1d}=120 h$
Therefore, there are 120 hours in 5 days.
TEMPERATURE
DEFINITION OF TEMPERATURE
Temperature is an attribute that describes how hot or cold an object or place is. Temperature is measured with the help of thermometer. While the metric system used Kelvin as a standard unit of measurement of temperature, people usually use Celsius (°C) or Fahrenheit (°F) to measure temperature.
CONVERSION OF TEMPERATURE
The table below shows the different formula in converting temperatures.

EXAMPLE #1
The temperature for today measures 28°C , what is its equivalent in Fahrenheit?
SOLUTION
Using the formula,
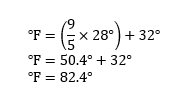
Therefore, 28°C is equivalent to 82.4°F.
EXAMPLE #2
What is 500 Kelvin converted to Celsius?
SOLUTION
Using the formula,
℃ = K – 273°
℃ = 500 – 273°
℃ = 227°
Therefore, 500 Kelvin is equal to 227.
Recommended Worksheets
Converting Like Measurement Units 5th Grade Math Worksheets
Converting Units of Measurement 4th Grade Math Worksheets
Word Problems Involving Measurements (Restaurant Themed) Math Worksheets









