What will I learn from this article?
After reading this article, you will be able to:
- define a vertical angle;
- state the vertical angle theorem;
- prove the vertical angle theorem;
- determine vertical angles in different figures; and
- solve problems involving vertical angles.
What is a vertical angle?
Vertical angles are pairs of opposite angles or non-adjacent angles formed by the intersection of two distinct lines. “Vertical” has become synonymous with “upright,” or the polar opposite of horizontal. However, in this case, it is more about the term “vertex.” Vertical angles get their name from the fact that they share a common vertex.
Vertical angles, in simple terms, are located opposite one another in the corners of “X,” formed by two straight lines. They are also referred to as vertically opposite angles due to their location being opposite to one another.
Say, for example,
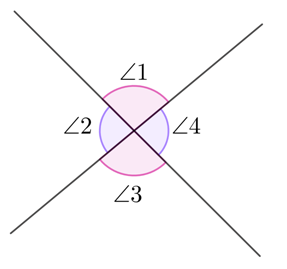
In the figure, ∠1 is vertically opposite to ∠3 and ∠2 is vertically opposite to ∠4. Additionally, we can observe that angles 1, 2, 3, and 4 all share the same vertex point.
What is the vertical angle theorem?
The vertical angle theorem states that:
If two intersecting straight lines formed angles that are opposite to each other, then they are congruent.
What is the proof of the vertical angle theorem?
Eudemus of Rhodes credited Thales of Miletus to the proof of the vertical angle theorem. The proposition demonstrated that because both pairs of vertical angles are supplementary to both adjacent angles, the vertical angles are equal in measure.
According to a historical note, Thales observed that when the Egyptians drew two intersecting lines, they measured the vertical angles to ensure they were equal. Thales concluded that one could establish that all vertical angles are equal if certain general propositions were accepted, such as:
- All straight angles are equal.
- Equals added to equals are equal.
- Equals subtracted from equal are equal.
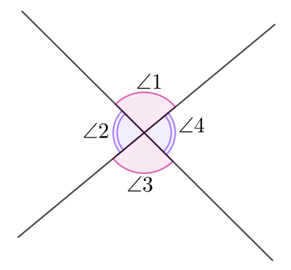
To prove the vertical angle theorem, suppose ∠1 and ∠2 are two adjacent angles that form a straight line. Then, by linear pair postulate, they are supplementary.
Thus, ∠1 + ∠2=180°.
Similarly, if ∠1 and ∠4 are two adjacent angles that form a straight line, ∠1 + ∠4=180°.
Then, by the transitive property of equality and by elimination,
∠1 + ∠2= ∠1 + ∠4
∠2=∠4
Since angles ∠1 and ∠3, ∠1 and ∠4 are adjacent angles, it follows the same statement that ∠1=∠3.
What are the facts about vertical angles?
The table below states other facts about vertical angles.
| Congruent Angles | Vertical angles are always equal. |
| Sum of Vertical Angles | Both pairs of vertical angles (4 angles that share the same vertex) always add up to 360°. |
| Adjacent Angles | The adjacent angles formed by each pair of vertical angles are supplementary (the sum of the angles is 180°. |
How to determine vertical angles?
To determine vertical angles, you must consider the following?
- Are the lines straight lines?
- Do the lines between them intersect each other?
- Do they share the same line?
- Do the angles share the same vertex?
Observe the examples of vertically opposite angles in the table below.
| Pair of Vertically Opposite Angles | Not a Pair of Vertical Angles |
 ∠1 and ∠2 are a pair of vertical angles since they share the same vertex and are opposite to each other. | 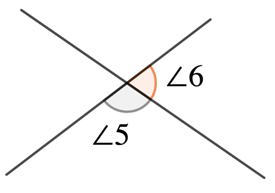 ∠5 and ∠6 are not a pair of vertical angles since they are not opposite to each other even though they share the same vertex. However, ∠5 and ∠6 are a pair of adjacent angles. |
 ∠3 and ∠4 are a pair of vertical angles since they share the same vertex and opposite each other. | 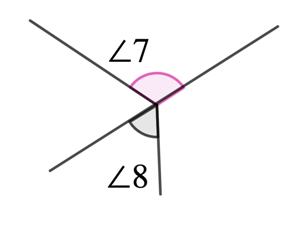 ∠7 and ∠8 are not a pair of vertical angles because even though they are opposite to each other and they share the same vertex, the two intersect lines is not a straight line. |
Example #1
Name the pair of vertical angles given in the figure below.

Solution
Given lines A and B that intersects at point P, the pair of vertical angles are:
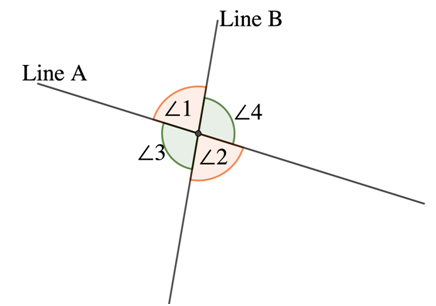
As shown in the figure, we can name the angles formed by intersecting two lines. Thus,
- ∠1 is vertically opposite to ∠2; and
- ∠3 is vertically opposite to ∠4 with the same vertex at point P.
Example #2
Name the angles formed when lines N and P intersect lines L and M. Determine the pairs of vertical angles in the figure below.
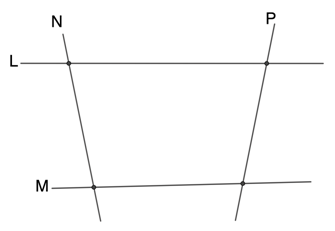
Solution
As shown in the figure, when lines N and P intersects with lines L and M, it creates 4 vertex points. Thus, we can name the angles created as:
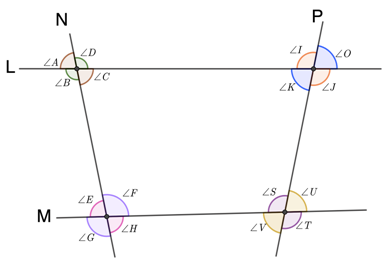
Therefore, based on the figure shown,
- ∠A is vertically opposite to angle ∠C;
- ∠B is vertically opposite to angle ∠D;
- Angles A, B, C, and D all have the same vertex point;
- ∠E is vertically opposite to angle ∠H;
- ∠G is vertically opposite to angle ∠F;
- Angles E, F, G, and H share the same vertex point;
- ∠I is vertically opposite to angle ∠J;
- ∠K is vertically opposite to angle ∠O;
- Angles I, J, K, and O have the same vertex point;
- ∠S is vertically opposite to angle ∠T;
- ∠U is vertically opposite to angle ∠V; and
- Angles S, T, U, and V share the same vertex point.
How do we solve problems involving vertical angles?
To solve problems involving vertical angles,
- Determine the pairs of vertical angles.
- Use the Vertical Angle theorem to relate the relationship between the measures of the vertical angles.
Example #1
Determine the value of x and the angle measures of the two angles, if the two angles are vertical angles.
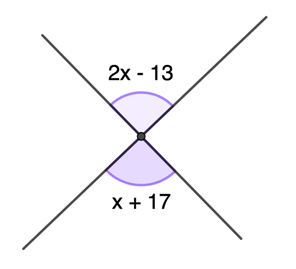
Solution
Step 1: Find the value of x. Since the two given angles are said to be vertical angles, then by vertical angle theorem:
2x – 13 = x + 17
2x – x = 17 + 13
x = 30
Step 2: Thus, the value of x is 30. By substitution, the measure of the two angles are:
- if ∠=2x-13, then
2x – 13 = 2 (30) – 13
= 60 – 13
= 47
- if ∠=x+17, then
x + 17 = 30 + 17
= 47
Since both of the angles measures 47°, then it is true that they are vertically opposite to each other.
Therefore, the value of x is 30 and the angle measure of the vertically opposite angle is 47°.
Example #2
If the flag of Jamaica forms pairs of vertically opposite angles, what is the value of x based on the given figure?

Solution
Step 1: Find the value of x. Since the angles formed are vertically opposite to each other, then by vertical angle theorem,
65° = 2x + 15°
2x = 65° – 15°
2x = 50°
$\frac{2x}{2} = \frac{(50°)}{2}$
x = 25°
Step 2: Check if 2x + 15 will come up with 65° if we substitute x = 25. Thus,
2x + 15 = 2(25) + 15
= 50 + 15
= 65
Therefore, the value of x is 25°.
Take note:
- Vertical angles always share the same vertex.
- Vertical angles are always equal.
- Vertical angles are always non-adjacent.
What is the significance of vertical angles?
Real-life settings where vertical angles are used include;
- railroad crossing sign,
- the letter “X’’, and
- open scissors pliers.
Vertical angles can also be found when a person crosses his arms in the shape of the alphabet X, and they can also be found very easily in flooring designs where lines intersect to form a pair of vertical angles. Another very common real-world example of vertically opposite angles is the dartboard’s intersecting lines, which help create ten pairs of vertical angles.
Recommended Worksheets
Understanding Supplementary, Complementary, Vertical and Adjacent Angles 7th Grade Math Worksheets
Reflex Angles (International Artists’ Day Themed) Math Worksheets
Obtuse Triangles (Toy Store Themed) Math Worksheets









